第三章 圆复习题---填空题(含解析)
图片预览



文档简介
北师大版数学九下第三章圆复习题---填空题
一.填空题
1.(2018秋?泉山区校级月考)点A、B在⊙O上,若∠AOB=40°,则∠OAB= .
2.(2018秋?灌云县校级月考)如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 度.
3.(2018秋?高港区校级月考)如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 .
4.(2018秋?海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
5.(2018?海南)如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
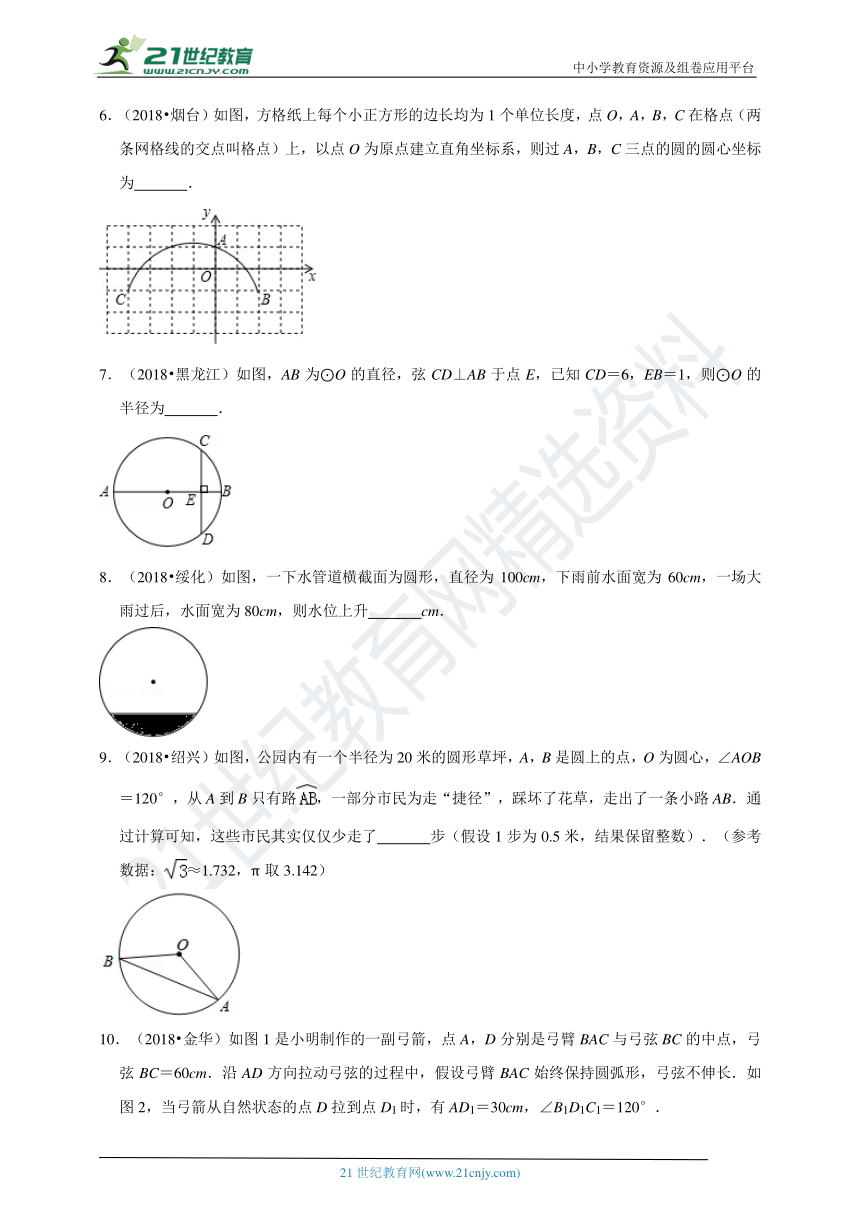
6.(2018?烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
7.(2018?黑龙江)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
8.(2018?绥化)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
9.(2018?绍兴)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)
10.(2018?金华)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
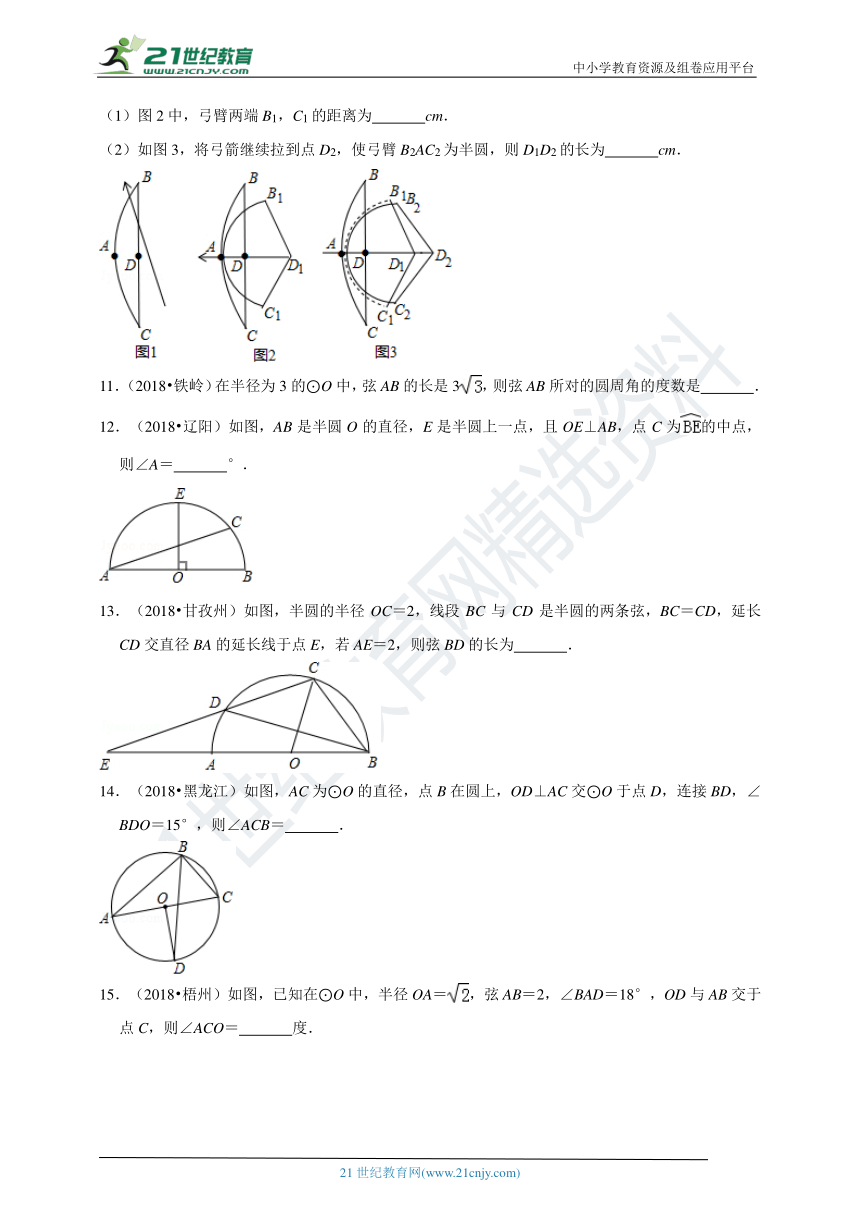
(1)图2中,弓臂两端B1,C1的距离为 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 cm.
11.(2018?铁岭)在半径为3的⊙O中,弦AB的长是3,则弦AB所对的圆周角的度数是 .
12.(2018?辽阳)如图,AB是半圆O的直径,E是半圆上一点,且OE⊥AB,点C为的中点,则∠A= °.
13.(2018?甘孜州)如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
14.(2018?黑龙江)如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= .
15.(2018?梧州)如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO= 度.
16.(2018?吉林)如图,A,B,C,D是⊙O上的四个点,=,若∠AOB=58°,则∠BDC= 度.
17.(2018?东莞市)同圆中,已知所对的圆心角是100°,则所对的圆周角是 .
18.(2018?杭州)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= .
19.(2018?青海)如图,A、B、C是⊙O上的三个点,若∠AOC=110°,则∠ABC= .
20.(2018?曲靖)如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE= °.
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
22.(2017?永州)如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC= 度.
23.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 .
24.(2018秋?丰县期中)平面内有一点P到圆上最远的距离是6,最近的距离是2,则圆的半径是 .
25.(2018秋?镇江期中)已知⊙O的半径为3cm,OP=4cm,A是OP的中点,则点A与⊙O的位置关系是点A在 .(填圆内、圆外或圆上)
26.(2017?宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
27.(2018秋?石景山区期末)如图,⊙O是正方形ABCD的外接圆,若E是上一点,则∠DEC= °.
28.(2018秋?丽江期末)已知一个三角形三边分别为13cm,12cm,5cm,则此三角形外接圆半径为 cm
29.(2018秋?潮南区期末)若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
30.(2018秋?綦江区校级期中)如图,△ABC内接于⊙O,若∠OAB=30°,则∠C= .
31.(2018秋?西城区期末)如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.
(1)点O到直线l距离的最大值为 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
32.(2017秋?江阴市期末)如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,连接MN,设直线y=x交MN于点G.若PG:PN=3:4,△PGN的周长为12,则△PON的周长是 .
33.(2018?益阳)如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 度.
34.(2018?巴中)如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 .
35.(2018?山西)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .
36.(2018?包头)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
37.(2018?东莞市)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
38.(2018?泰州)如图,△ABC中,∠ACB=90°,sinA=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
39.(2018秋?如皋市期中)如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为 .
40.(2018秋?江都区期中)如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 .
41.(2018?南京)如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C
旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点
F,则CF的长为 .
42.(2018秋?伊通县期末)如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为 .
43.(2018秋?临洮县期末)如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 .
44.(2018秋?长春期末)如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .
45.(2017秋?仙居县期末)已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是 .
46.(2018?郴州)如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为 cm.(结果用π表示)
47.(2018?盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
48.(2018?永州)如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则的长为 .
49.(2018秋?庆阳期末)如图,在△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=2,则扇形BDE的面积为 .
50.(2018春?郓城县期中)在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是 cm2.
北师大版数学九下第三章圆复习题---填空题
参考答案与试题解析
一.填空题(共50小题)
1.(2018秋?泉山区校级月考)点A、B在⊙O上,若∠AOB=40°,则∠OAB= 70° .
【分析】由∠AOB=40°,OA=OB知∠OAB=∠OBA=,代入计算可得.
【解答】解:如图,
∵∠AOB=40°,OA=OB,
∴∠OAB=∠OBA==70°,
故答案为:70°.
2.(2018秋?灌云县校级月考)如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 60 度.
【分析】根据同圆的半径相等和等腰三角形的性质可得∠COB=∠C=40°,根据外角的性质得∠ABO=80°,所以∠A=80°,最后根据三角形的内角和定理可得结论.
【解答】解:连接OB,
∵OB=OE=BC,∠C=40°,
∴∠COB=∠C=40°,
∴∠ABO=∠C+∠COB=80°,
∵OA=OB,
∴∠A=∠ABO=80°,
△AOC中,∠EOA=180°﹣40°﹣80°=60°,
故答案为:60.
3.(2018秋?高港区校级月考)如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 48° .
【分析】可求得∠BOC=∠EOD=∠COD=32°,继而可求得∠AOE的度数;然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
【解答】解:∵,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=84°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣84°)=48°.
故答案为:48°
4.(2018秋?海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 ①③ (填序号).
【分析】如图,连接OC,设OB交CD于K.利用全等三角形的性质以及圆周角定理一一判断即可;
【解答】解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,显然不可能成立,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
5.(2018?海南)如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 (2,6) .
【分析】过点M作MF⊥CD于点F,则CF=CD=8,过点C作CE⊥OA于点E,由勾股定理可求得MF的长,从而得出OE的长,然后写出点C的坐标.
【解答】解:∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
6.(2018?烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 (﹣1,﹣2) .
【分析】连接CB,作CB的垂直平分线,根据勾股定理和半径相等得出点O的坐标即可.
【解答】解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,
CD═DB=DA=,
所以D是过A,B,C三点的圆的圆心,
即D的坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2),
7.(2018?黑龙江)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 5 .
【分析】连接OC,由垂径定理知,点E是CD的中点,CE=CD,在直角△OCE中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.
【解答】解:连接OC,
∵AB为⊙O的直径,AB⊥CD,
∴CE=DE=CD=×6=3,
设⊙O的半径为xcm,
则OC=xcm,OE=OB﹣BE=x﹣1,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=32+(x﹣1)2,
解得:x=5,
∴⊙O的半径为5,
故答案为:5.
8.(2018?绥化)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 10或70 cm.
【分析】分两种情形分别求解即可解决问题;
【解答】解:作半径OD⊥AB于C,连接OB
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下时 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
9.(2018?绍兴)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了 15 步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)
【分析】作OC⊥AB于C,如图,根据垂径定理得到AC=BC,再利用等腰三角形的性质和三角形内角和计算出∠A=30°,则OC=10,AC=10,所以AB≈69(步),然后利用弧长公式计算出的长,最后求它们的差即可.
【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B=(180°﹣∠AOB)=(180°﹣120°)=30°,
在Rt△AOC中,OC=OA=10,AC=OC=10,
∴AB=2AC=20≈69(步);
而的长=≈84(步),
的长与AB的长多15步.
所以这些市民其实仅仅少走了 15步.
故答案为15.
10.(2018?金华)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为 30 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 10﹣10 cm.
【分析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
【解答】解:(1)如图2中,连接B1C1交DD1于H.
∵D1A=D1B1=30
∴D1是的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15,
∴B1C1=30
∴弓臂两端B1,C1的距离为30
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=,
∴r=20,
∴AG=GB2=20,GD1=30﹣20=10,
在Rt△GB2D2中,GD2==10
∴D1D2=10﹣10.
故答案为30,10﹣10,
11.(2018?铁岭)在半径为3的⊙O中,弦AB的长是3,则弦AB所对的圆周角的度数是 60°或120° .
【分析】先根据题意画出图形,连接OA、OB,过O作OF⊥AB,由垂径可求出AF的长,根据特殊角的三角函数值可求出∠AOF的度数,由圆周角定理及圆内接四边形的性质即可求出答案.
【解答】解:如图所示,
连接OA、OB,过O作OF⊥AB,则AF=AB,∠AOF=∠AOB,
∵OA=3,AB=3,
∴AF=AB=,
∴sin∠AOF==,
∴∠AOF=60°,
∴∠AOB=2∠AOF=120°,
∴∠ADB=∠AOB=×120°=60°,
∴∠AEB=180°﹣60°=120°.
故答案为:60°或120°.
12.(2018?辽阳)如图,AB是半圆O的直径,E是半圆上一点,且OE⊥AB,点C为的中点,则∠A= 22.5 °.
【分析】连接半径OC,先根据点C为的中点,得∠BOC=45°,再由同圆的半径相等和等腰三角形的性质得:∠A=∠ACO=×45°,可得结论.
【解答】解:连接OC,
∵OE⊥AB,
∴∠EOB=90°,
∵点C为的中点,
∴∠BOC=45°,
∵OA=OC,
∴∠A=∠ACO=×45°=22.5°,
故答案为:22.5°.
13.(2018?甘孜州)如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
【分析】连接OD,AD,根据OC平分∠BCD,BC=DC,即可得到BD⊥CO,依据AB是直径,可得AD⊥BD,进而得出AD=CO=1,再根据Rt△ABD,利用勾股定理可得BD=.
【解答】 解:如图,连接OD,AD,
∵BC=DC,BO=DO,
∴∠BDC=∠DBC,∠BDO=∠DBO,
∴∠CDO=∠CBO,
又∵OC=OB=OD,
∴∠BCO=∠DCO,即OC平分∠BCD,
又∵BC=DC,
∴BD⊥CO,
又∵AB是直径,
∴AD⊥BD,
∴AD∥CO,
又∵AE=AO=2,
∴AD=CO=1,
∴Rt△ABD中,BD===.
故答案为:.
14.(2018?黑龙江)如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= 60° .
【分析】连接DC,得出∠BDC的度数,进而得出∠A的度数,利用互余解答即可.
【解答】解:连接DC,
∵AC为⊙O的直径,OD⊥AC,
∴∠DOC=90°,∠ABC=90°,
∵OD=OC,
∴∠ODC=45°,
∵∠BDO=15°,
∴∠BDC=30°,
∴∠A=30°,
∴∠ACB=60°,
故答案为:60°.
15.(2018?梧州)如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO= 81 度.
【分析】根据勾股定理的逆定理可以判断△AOB的形状,由圆周角定理可以求得∠BOD的度数,再根据三角形的外角和不相邻的内角的关系,即可求得∠AOC的度数.
【解答】解:∵OA=,OB=,AB=2,
∴OA2+OB2=AB2,OA=OB,
∴△AOB是等腰直角三角形,∠AOB=90°,
∴∠OBA=45°,
∵∠BAD=18°,
∴∠BOD=36°,
∴∠ACO=∠OBA+∠BOD=45°+36°=81°,
故答案为:81.
16.(2018?吉林)如图,A,B,C,D是⊙O上的四个点,=,若∠AOB=58°,则∠BDC= 29 度.
【分析】根据∠BDC=∠BOC求解即可;
【解答】解:连接OC.
∵=,
∴∠AOB=∠BOC=58°,
∴∠BDC=∠BOC=29°,
故答案为29.
17.(2018?东莞市)同圆中,已知所对的圆心角是100°,则所对的圆周角是 50° .
【分析】直接利用圆周角定理求解.
【解答】解:弧AB所对的圆心角是100°,则弧AB所对的圆周角为50°.
故答案为50°.
18.(2018?杭州)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= 30° .
【分析】利用垂径定理和三角函数得出∠CDO=30°,进而得出∠DOA=60°,利用圆周角定理得出∠DFA=30°即可.
【解答】解:∵点C是半径OA的中点,
∴OC=OD,
∵DE⊥AB,
∴∠CDO=30°,
∴∠DOA=60°,
∴∠DFA=30°,
故答案为:30°
19.(2018?青海)如图,A、B、C是⊙O上的三个点,若∠AOC=110°,则∠ABC= 125° .
【分析】首先在优弧AC上取点D,连接AD,CD,由由圆周角定理,可求得∠ADC的度数,又由圆的内接四边形的性质,求得∠ABC的度数.
【解答】解:如图,在优弧AC上取点D,连接AD,CD,
∵∠AOC=100°,
∴∠ADC=∠AOC=55°,
∴∠ABC=180°﹣∠ADC=125°.
故答案为:125°.
20.(2018?曲靖)如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE= n °.
【分析】利用圆内接四边形的对角互补和邻补角的性质求解.
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠DCB=180°,
又∵∠DCE+∠DCB=180°
∴∠DCE=∠A=n°
故答案为:n
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= 70° .
【分析】直接利用圆周角定理以及结合三角形内角和定理得出∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC,进而得出答案.
【解答】解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
22.(2017?永州)如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC= 100 度.
【分析】先求出∠AEC,再用圆内接四边形的性质即可得出结论.
【解答】解:如图,
连接AE,
∵点D是的中点,
∴∠AED=∠CED,
∵∠CED=40°,
∴∠AEC=2∠CED=80°,
∵四边形ADCE是圆内接四边形,
∴∠ADC+∠AEC=180°,
∴∠ADC=180°﹣∠AEC=100°,
故答案为:100.
23.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 x<3 .
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
∵点A、B、C三点都在圆外,
∴x<3.
故答案为:x<3;
24.(2018秋?丰县期中)平面内有一点P到圆上最远的距离是6,最近的距离是2,则圆的半径是 2或4 .
【分析】分两种情况:点在圆外,直径等于两个距离的差;点在圆内,直径等于两个距离的和.
【解答】解:∵点P到⊙O的最近距离为2,最远距离为6,则:
当点在圆外时,则⊙O的直径为6﹣2=4,半径是2;
当点在圆内时,则⊙O的直径是6+2=8,半径为4,
综上,圆的半径是2或4,
故答案为:2或4.
25.(2018秋?镇江期中)已知⊙O的半径为3cm,OP=4cm,A是OP的中点,则点A与⊙O的位置关系是点A在 圆内 .(填圆内、圆外或圆上)
【分析】知道OP的长,点A是OP的中点,得到OA的长与半径的关系,求出点A与圆的位置关系.
【解答】解:因为OP=4cm,A是线段OP的中点,所以OA=2cm,小于圆的半径,因此点A在圆内.
故答案为:圆内.
26.(2017?宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 5 .
【分析】根据圆的确定先做出过A,B,C三点的外接圆,从而得出答案.
【解答】解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
27.(2018秋?石景山区期末)如图,⊙O是正方形ABCD的外接圆,若E是上一点,则∠DEC= 45 °.
【分析】连接OD、OC,如图,根据正方形的性质得到∠COD=90°,然后根据圆周角定理得到∠CED的度数.
【解答】解:连接OD、OC,如图,
∵⊙O是正方形ABCD的外接圆,
∴∠COD=90°,
∴∠COD=90°,
∴∠CED=∠COD=45°.
故答案为45.
28.(2018秋?丽江期末)已知一个三角形三边分别为13cm,12cm,5cm,则此三角形外接圆半径为 6.5 cm
【分析】首先得出三角形是直角三角形,再根据直角三角形的斜边为它的外接圆的直径得到这个三角形的外接圆的半径.
【解答】解:∵52+122=132,
∴此三角形是直角三角形,
因为直角三角形的斜边为它的外接圆的直径,
所以这个三角形的外接圆的半径是6.5cm.
故答案为:6.5.
29.(2018秋?潮南区期末)若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
【分析】首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
【解答】解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB===30°,
∵⊙O的半径为2,
∴OB=2,
∴BD=OB?cos∠OBD=2×cos30°=2×=,
∴BC=2BD=2.
∴等边△ABC的边长为2.
故答案为:2.
30.(2018秋?綦江区校级期中)如图,△ABC内接于⊙O,若∠OAB=30°,则∠C= 60° .
【分析】根据等腰三角形的性质,三角形内角和定理求出∠AOB,根据圆周角定理解答.
【解答】解:∵OA=OB,
∴∠OBA=∠OAB=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
由圆周角定理得,∠C=∠AOB=60°,
故答案为:60°.
31.(2018秋?西城区期末)如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.
(1)点O到直线l距离的最大值为 7 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
【分析】(1)如图1,当点P在圆外且O,A,P三点共线时,点O到直线l距离的最大,于是得到结论;
(2)如图2,根据已知条件得到线段MN是⊙O的直径,根据勾股定理即可得到结论.
【解答】解:(1)如图1,∵l⊥PA,
∴当点P在圆外且O,A,P三点共线时,点O到直线l距离的最大,
最大值为AO+AP=5+2=7;
(2)如图2,∵M,N是直线l与⊙O的公共点,当线段MN的长度最大时,
线段MN是⊙O的直径,
∵l⊥PA,
∴∠AOO=90°,
∵AP=2,OA=5,
∴OP==,
故答案为:7,.
32.(2017秋?江阴市期末)如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,连接MN,设直线y=x交MN于点G.若PG:PN=3:4,△PGN的周长为12,则△PON的周长是 16或18﹣2 .
【分析】根据圆周角定理得到∠MPN=90°,推出∠MOP=∠NOP=45°,得到PM=PN,设PG=3x,PN=4x,得到PM=4x,根据勾股定理得到MN=4x,根据相似三角形的性质得到PO=x,NG=2x+x或NG=2x﹣x,根据三角形的周长公式列方程3x+4x+2x+x=12或3x+4x+2x﹣x=12,求得x=或x=,当x=时,当x=时,根据三角形的周长公式得到结论.
【解答】解:∵∠MON=90°,
∴MN是直径,
∴∠MPN=90°,
∵直线y=x是∠MON的平分线,
∴∠MOP=∠NOP=45°,
∴=,
∴PM=PN,
∵PG:PN=3:4,
∴设PG=3x,PN=4x,
∴PM=4x,
∴MN=4x,
∵∠PNM=∠PON=45°,
∠NPG=∠OPN,
∴△PGN∽△PNO,
∴,
∴=,
∴PO=x,
∴OG=PO﹣PG=x,
∵∠OMN=∠NPO,
∴△OMG∽△NPG,
∴,
∴=,
∴NG=2x+x或NG=2x﹣x,
∵△PGN的周长为12,
∴3x+4x+2x+x=12或3x+4x+2x﹣x=12,
解得:x=或x=,
∴当x=时,PO=×,PN=4×,GN=(2+1)×,
∵△PGN∽△PNO,
∴==,
∴ON=×(2+1)×,
∴△PON的周长=PO+PN+ON=×+4×+×(2+1)×=16,
同理当x=时,△PON的周长=18﹣2.
综上所述,△PON的周长是16或18﹣2.
故答案为:16或18﹣2.
33.(2018?益阳)如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 45 度.
【分析】利用圆周角定理得到∠ADB=90°,再根据切线的性质得∠ABC=90°,然后根据等腰三角形的判定方法得到△ABC为等腰直角三角形,从而得到∠C的度数.
【解答】解:∵AB为直径,
∴∠ADB=90°,
∵BC为切线,
∴AB⊥BC,
∴∠ABC=90°,
∵AD=CD,
∴△ABC为等腰直角三角形,
∴∠C=45°.
故答案为45.
34.(2018?巴中)如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 8﹣2π .
【分析】由半圆的直径为4且与矩形一边BC相切可得矩形的宽AB=2,再根据阴影部分面积=矩形面积﹣半圆面积求解可得.
【解答】解:∵半圆的直径AD=4,且与BC相切,
∴半径为2,AB=2,
∴图中的阴影部分的面积为4×2﹣?π?22=8﹣2π,
故答案为:8﹣2π.
35.(2018?山西)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .
【分析】先利用勾股定理求出AB=10,进而求出CD=BD=5,再求出CF=4,进而求出DF=3,再判断出FG⊥BD,利用面积即可得出结论.
【解答】解:如图,
在Rt△ABC中,根据勾股定理得,AB=10,
∴点D是AB中点,
∴CD=BD=AB=5,
连接DF,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴BF=CF=BC=4,
∴DF==3,
连接OF,
∵OC=OD,CF=BF,
∴OF∥AB,
∴∠OFC=∠B,
∵FG是⊙O的切线,
∴∠OFG=90°,
∴∠OFC+∠BFG=90°,
∴∠BFG+∠B=90°,
∴FG⊥AB,
∴S△BDF=DF×BF=BD×FG,
∴FG===,
故答案为.
36.(2018?包头)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 115 度.
【分析】连接OC,根据切线的性质求出∠DCO,求出∠COB,即可求出答案.
【解答】解:
连接OC,
∵DC切⊙O于C,
∴∠DCO=90°,
∵∠D=40°,
∴∠COB=∠D+∠DCO=130°,
∴的度数是130°,
∴的度数是360°﹣130°=230°,
∴∠BEC==115°,
故答案为:115.
37.(2018?东莞市)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 π .(结果保留π)
【分析】连接OE,如图,利用切线的性质得OD=2,OE⊥BC,易得四边形OECD为正方形,先利用扇形面积公式,利用S正方形OECD﹣S扇形EOD计算由弧DE、线段EC、CD所围成的面积,然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积.
【解答】解:连接OE,如图,
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
易得四边形OECD为正方形,
∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣=4﹣π,
∴阴影部分的面积=×2×4﹣(4﹣π)=π.
故答案为π.
38.(2018?泰州)如图,△ABC中,∠ACB=90°,sinA=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 或 .
【分析】分两种情形分别求解:如图1中,当⊙P与直线AC相切于点Q时,如图2中,当⊙P与AB相切于点T时,
【解答】解:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.
设PQ=PA′=r,
∵PQ∥CA′,
∴=,
∴=,
∴r=.
如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,
∵△A′BT∽△ABC,
∴=,
∴=,
∴A′T=,
∴r=A′T=.
综上所述,⊙P的半径为或.
39.(2018秋?如皋市期中)如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为 8 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=10,BC=B′C=8,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=5,继而求得CG=B′E=OH==4,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=10,BC=B′C=8,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=5,
∴B′H=OE=5,
∴CH=B′C﹣B′H=3,
∴CG=B′E=OH==4,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=8,
故答案为:8.
40.(2018秋?江都区期中)如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 4 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=6,BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=3,继而求得CG=B′E=OH==2,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=3,
∴B′H=OE=3,
∴CH=B′C﹣B′H=1,
∴CG=B′E=OH==2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
41.(2018?南京)如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C
旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点
F,则CF的长为 4 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=5、BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=2.5,继而求得CG=B′E=OH===2,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,
∴B′H=OE=2.5,
∴CH=B′C﹣B′H=1.5,
∴CG=B′E=OH===2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
42.(2018秋?伊通县期末)如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为 110° .
【分析】根据三角形的内心的概念得到∠OBC=∠ABC=30°,∠OCB=∠ACB=40°,根据三角形内角和定理计算即可.
【解答】解:∵⊙O是△ABC的内切圆,
∴∠OBC=∠ABC=30°,∠OCB=∠ACB=40°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=110°,
故答案为:110°.
43.(2018秋?临洮县期末)如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 16cm .
【分析】根据切线的性质,得到直角三角形OAP,根据勾股定理求得PA的长;根据切线长定理,得BD=CD,CE=AE,PA=PB,从而求解.
【解答】解:连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
在直角三角形OAP中,根据勾股定理,得AP=8,
∴△PDE的周长为2AP=16.
故选答案为16cm.
44.(2018秋?长春期末)如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= 30° .
【分析】连接OB,AD,BD,由多边形是正六边形可求出∠AOB的度数,再根据圆周角定理即可求出∠ADB的度数,利用弦切角定理求出∠PAB即可.
【解答】解:连接OB,AD,BD,
∵多边形ABCDEF是正多边形,
∴AD为外接圆的直径,
∠AOB==60°,
∴∠ADB=∠AOB=×60°=30°.
∵直线PA与⊙O相切于点A,
∴∠PAB=∠ADB=30°.
故答案为:30°.
45.(2017秋?仙居县期末)已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是 4﹣2 .
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于4﹣2小于等于4,由此即可判断.
【解答】解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于4﹣2小于等于4,
∴B,M之间距离的最小值是4﹣2.
故答案为:4﹣2.
46.(2018?郴州)如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为 12π cm.(结果用π表示)
【分析】根据圆锥的展开图为扇形,结合圆周长公式的求解.
【解答】解:设底面圆的半径为rcm,
由勾股定理得:r==6,
∴2πr=2π×6=12π,
故答案为:12π.
47.(2018?盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
【分析】先根据图1确定:图2的周长=2个的长,根据弧长公式可得结论.
【解答】解:由图1得:的长+的长=的长
∵半径OA=2cm,∠AOB=120°
则图2的周长为:=
故答案为:.
48.(2018?永州)如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则的长为 .
【分析】由点A(1,1),可得OA==,点A在第一象限的角平分线上,那么∠AOB=45°,再根据弧长公式计算即可.
【解答】解:∵点A(1,1),
∴OA==,点A在第一象限的角平分线上,
∵以点O为旋转中心,将点A逆时针旋转到点B的位置,
∴∠AOB=45°,
∴的长为=.
故答案为.
49.(2018秋?庆阳期末)如图,在△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=2,则扇形BDE的面积为 .
【分析】根据三角形内角和定理求出∠C,根据三角形的外角的性质求出∠BDE,根据扇形面积公式计算.
【解答】解:∵∠A=60°,∠B=100°,
∴∠C=20°,
∵BD=DC=1,DE=DB,
∴DE=DC=1,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积==,
故答案为:.
50.(2018春?郓城县期中)在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是 12π cm2.
【分析】直接利用扇形面积公式代入求出面积即可.
【解答】解:∵在圆心角为120°的扇形AOB中,半径OA=6cm,
∴扇形OAB的面积是:=12π(cm2),
故答案为12π.
一.填空题
1.(2018秋?泉山区校级月考)点A、B在⊙O上,若∠AOB=40°,则∠OAB= .
2.(2018秋?灌云县校级月考)如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 度.
3.(2018秋?高港区校级月考)如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 .
4.(2018秋?海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
5.(2018?海南)如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
6.(2018?烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
7.(2018?黑龙江)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
8.(2018?绥化)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
9.(2018?绍兴)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)
10.(2018?金华)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 cm.
11.(2018?铁岭)在半径为3的⊙O中,弦AB的长是3,则弦AB所对的圆周角的度数是 .
12.(2018?辽阳)如图,AB是半圆O的直径,E是半圆上一点,且OE⊥AB,点C为的中点,则∠A= °.
13.(2018?甘孜州)如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
14.(2018?黑龙江)如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= .
15.(2018?梧州)如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO= 度.
16.(2018?吉林)如图,A,B,C,D是⊙O上的四个点,=,若∠AOB=58°,则∠BDC= 度.
17.(2018?东莞市)同圆中,已知所对的圆心角是100°,则所对的圆周角是 .
18.(2018?杭州)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= .
19.(2018?青海)如图,A、B、C是⊙O上的三个点,若∠AOC=110°,则∠ABC= .
20.(2018?曲靖)如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE= °.
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
22.(2017?永州)如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC= 度.
23.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 .
24.(2018秋?丰县期中)平面内有一点P到圆上最远的距离是6,最近的距离是2,则圆的半径是 .
25.(2018秋?镇江期中)已知⊙O的半径为3cm,OP=4cm,A是OP的中点,则点A与⊙O的位置关系是点A在 .(填圆内、圆外或圆上)
26.(2017?宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
27.(2018秋?石景山区期末)如图,⊙O是正方形ABCD的外接圆,若E是上一点,则∠DEC= °.
28.(2018秋?丽江期末)已知一个三角形三边分别为13cm,12cm,5cm,则此三角形外接圆半径为 cm
29.(2018秋?潮南区期末)若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
30.(2018秋?綦江区校级期中)如图,△ABC内接于⊙O,若∠OAB=30°,则∠C= .
31.(2018秋?西城区期末)如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.
(1)点O到直线l距离的最大值为 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
32.(2017秋?江阴市期末)如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,连接MN,设直线y=x交MN于点G.若PG:PN=3:4,△PGN的周长为12,则△PON的周长是 .
33.(2018?益阳)如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 度.
34.(2018?巴中)如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 .
35.(2018?山西)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .
36.(2018?包头)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
37.(2018?东莞市)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
38.(2018?泰州)如图,△ABC中,∠ACB=90°,sinA=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
39.(2018秋?如皋市期中)如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为 .
40.(2018秋?江都区期中)如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 .
41.(2018?南京)如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C
旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点
F,则CF的长为 .
42.(2018秋?伊通县期末)如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为 .
43.(2018秋?临洮县期末)如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 .
44.(2018秋?长春期末)如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .
45.(2017秋?仙居县期末)已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是 .
46.(2018?郴州)如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为 cm.(结果用π表示)
47.(2018?盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
48.(2018?永州)如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则的长为 .
49.(2018秋?庆阳期末)如图,在△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=2,则扇形BDE的面积为 .
50.(2018春?郓城县期中)在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是 cm2.
北师大版数学九下第三章圆复习题---填空题
参考答案与试题解析
一.填空题(共50小题)
1.(2018秋?泉山区校级月考)点A、B在⊙O上,若∠AOB=40°,则∠OAB= 70° .
【分析】由∠AOB=40°,OA=OB知∠OAB=∠OBA=,代入计算可得.
【解答】解:如图,
∵∠AOB=40°,OA=OB,
∴∠OAB=∠OBA==70°,
故答案为:70°.
2.(2018秋?灌云县校级月考)如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 60 度.
【分析】根据同圆的半径相等和等腰三角形的性质可得∠COB=∠C=40°,根据外角的性质得∠ABO=80°,所以∠A=80°,最后根据三角形的内角和定理可得结论.
【解答】解:连接OB,
∵OB=OE=BC,∠C=40°,
∴∠COB=∠C=40°,
∴∠ABO=∠C+∠COB=80°,
∵OA=OB,
∴∠A=∠ABO=80°,
△AOC中,∠EOA=180°﹣40°﹣80°=60°,
故答案为:60.
3.(2018秋?高港区校级月考)如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 48° .
【分析】可求得∠BOC=∠EOD=∠COD=32°,继而可求得∠AOE的度数;然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
【解答】解:∵,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=84°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣84°)=48°.
故答案为:48°
4.(2018秋?海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 ①③ (填序号).
【分析】如图,连接OC,设OB交CD于K.利用全等三角形的性质以及圆周角定理一一判断即可;
【解答】解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,显然不可能成立,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
5.(2018?海南)如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 (2,6) .
【分析】过点M作MF⊥CD于点F,则CF=CD=8,过点C作CE⊥OA于点E,由勾股定理可求得MF的长,从而得出OE的长,然后写出点C的坐标.
【解答】解:∵四边形OCDB是平行四边形,B(16,0),
∴CD∥OA,CD=OB=16,
过点M作MF⊥CD于点F,则CF=CD=8,
过点C作CE⊥OA于点E,
∵A(20,0),
∴OE=OM﹣ME=OM﹣CF=10﹣8=2.
连接MC,则MC=OA=10,
∴在Rt△CMF中,由勾股定理得MF==6
∴点C的坐标为(2,6)
故答案为:(2,6).
6.(2018?烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 (﹣1,﹣2) .
【分析】连接CB,作CB的垂直平分线,根据勾股定理和半径相等得出点O的坐标即可.
【解答】解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,
CD═DB=DA=,
所以D是过A,B,C三点的圆的圆心,
即D的坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2),
7.(2018?黑龙江)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 5 .
【分析】连接OC,由垂径定理知,点E是CD的中点,CE=CD,在直角△OCE中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.
【解答】解:连接OC,
∵AB为⊙O的直径,AB⊥CD,
∴CE=DE=CD=×6=3,
设⊙O的半径为xcm,
则OC=xcm,OE=OB﹣BE=x﹣1,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=32+(x﹣1)2,
解得:x=5,
∴⊙O的半径为5,
故答案为:5.
8.(2018?绥化)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 10或70 cm.
【分析】分两种情形分别求解即可解决问题;
【解答】解:作半径OD⊥AB于C,连接OB
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下时 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
9.(2018?绍兴)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了 15 步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)
【分析】作OC⊥AB于C,如图,根据垂径定理得到AC=BC,再利用等腰三角形的性质和三角形内角和计算出∠A=30°,则OC=10,AC=10,所以AB≈69(步),然后利用弧长公式计算出的长,最后求它们的差即可.
【解答】解:作OC⊥AB于C,如图,
则AC=BC,
∵OA=OB,
∴∠A=∠B=(180°﹣∠AOB)=(180°﹣120°)=30°,
在Rt△AOC中,OC=OA=10,AC=OC=10,
∴AB=2AC=20≈69(步);
而的长=≈84(步),
的长与AB的长多15步.
所以这些市民其实仅仅少走了 15步.
故答案为15.
10.(2018?金华)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为 30 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 10﹣10 cm.
【分析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
【解答】解:(1)如图2中,连接B1C1交DD1于H.
∵D1A=D1B1=30
∴D1是的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15,
∴B1C1=30
∴弓臂两端B1,C1的距离为30
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=,
∴r=20,
∴AG=GB2=20,GD1=30﹣20=10,
在Rt△GB2D2中,GD2==10
∴D1D2=10﹣10.
故答案为30,10﹣10,
11.(2018?铁岭)在半径为3的⊙O中,弦AB的长是3,则弦AB所对的圆周角的度数是 60°或120° .
【分析】先根据题意画出图形,连接OA、OB,过O作OF⊥AB,由垂径可求出AF的长,根据特殊角的三角函数值可求出∠AOF的度数,由圆周角定理及圆内接四边形的性质即可求出答案.
【解答】解:如图所示,
连接OA、OB,过O作OF⊥AB,则AF=AB,∠AOF=∠AOB,
∵OA=3,AB=3,
∴AF=AB=,
∴sin∠AOF==,
∴∠AOF=60°,
∴∠AOB=2∠AOF=120°,
∴∠ADB=∠AOB=×120°=60°,
∴∠AEB=180°﹣60°=120°.
故答案为:60°或120°.
12.(2018?辽阳)如图,AB是半圆O的直径,E是半圆上一点,且OE⊥AB,点C为的中点,则∠A= 22.5 °.
【分析】连接半径OC,先根据点C为的中点,得∠BOC=45°,再由同圆的半径相等和等腰三角形的性质得:∠A=∠ACO=×45°,可得结论.
【解答】解:连接OC,
∵OE⊥AB,
∴∠EOB=90°,
∵点C为的中点,
∴∠BOC=45°,
∵OA=OC,
∴∠A=∠ACO=×45°=22.5°,
故答案为:22.5°.
13.(2018?甘孜州)如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
【分析】连接OD,AD,根据OC平分∠BCD,BC=DC,即可得到BD⊥CO,依据AB是直径,可得AD⊥BD,进而得出AD=CO=1,再根据Rt△ABD,利用勾股定理可得BD=.
【解答】 解:如图,连接OD,AD,
∵BC=DC,BO=DO,
∴∠BDC=∠DBC,∠BDO=∠DBO,
∴∠CDO=∠CBO,
又∵OC=OB=OD,
∴∠BCO=∠DCO,即OC平分∠BCD,
又∵BC=DC,
∴BD⊥CO,
又∵AB是直径,
∴AD⊥BD,
∴AD∥CO,
又∵AE=AO=2,
∴AD=CO=1,
∴Rt△ABD中,BD===.
故答案为:.
14.(2018?黑龙江)如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= 60° .
【分析】连接DC,得出∠BDC的度数,进而得出∠A的度数,利用互余解答即可.
【解答】解:连接DC,
∵AC为⊙O的直径,OD⊥AC,
∴∠DOC=90°,∠ABC=90°,
∵OD=OC,
∴∠ODC=45°,
∵∠BDO=15°,
∴∠BDC=30°,
∴∠A=30°,
∴∠ACB=60°,
故答案为:60°.
15.(2018?梧州)如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO= 81 度.
【分析】根据勾股定理的逆定理可以判断△AOB的形状,由圆周角定理可以求得∠BOD的度数,再根据三角形的外角和不相邻的内角的关系,即可求得∠AOC的度数.
【解答】解:∵OA=,OB=,AB=2,
∴OA2+OB2=AB2,OA=OB,
∴△AOB是等腰直角三角形,∠AOB=90°,
∴∠OBA=45°,
∵∠BAD=18°,
∴∠BOD=36°,
∴∠ACO=∠OBA+∠BOD=45°+36°=81°,
故答案为:81.
16.(2018?吉林)如图,A,B,C,D是⊙O上的四个点,=,若∠AOB=58°,则∠BDC= 29 度.
【分析】根据∠BDC=∠BOC求解即可;
【解答】解:连接OC.
∵=,
∴∠AOB=∠BOC=58°,
∴∠BDC=∠BOC=29°,
故答案为29.
17.(2018?东莞市)同圆中,已知所对的圆心角是100°,则所对的圆周角是 50° .
【分析】直接利用圆周角定理求解.
【解答】解:弧AB所对的圆心角是100°,则弧AB所对的圆周角为50°.
故答案为50°.
18.(2018?杭州)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= 30° .
【分析】利用垂径定理和三角函数得出∠CDO=30°,进而得出∠DOA=60°,利用圆周角定理得出∠DFA=30°即可.
【解答】解:∵点C是半径OA的中点,
∴OC=OD,
∵DE⊥AB,
∴∠CDO=30°,
∴∠DOA=60°,
∴∠DFA=30°,
故答案为:30°
19.(2018?青海)如图,A、B、C是⊙O上的三个点,若∠AOC=110°,则∠ABC= 125° .
【分析】首先在优弧AC上取点D,连接AD,CD,由由圆周角定理,可求得∠ADC的度数,又由圆的内接四边形的性质,求得∠ABC的度数.
【解答】解:如图,在优弧AC上取点D,连接AD,CD,
∵∠AOC=100°,
∴∠ADC=∠AOC=55°,
∴∠ABC=180°﹣∠ADC=125°.
故答案为:125°.
20.(2018?曲靖)如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE= n °.
【分析】利用圆内接四边形的对角互补和邻补角的性质求解.
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠DCB=180°,
又∵∠DCE+∠DCB=180°
∴∠DCE=∠A=n°
故答案为:n
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= 70° .
【分析】直接利用圆周角定理以及结合三角形内角和定理得出∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC,进而得出答案.
【解答】解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
22.(2017?永州)如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC= 100 度.
【分析】先求出∠AEC,再用圆内接四边形的性质即可得出结论.
【解答】解:如图,
连接AE,
∵点D是的中点,
∴∠AED=∠CED,
∵∠CED=40°,
∴∠AEC=2∠CED=80°,
∵四边形ADCE是圆内接四边形,
∴∠ADC+∠AEC=180°,
∴∠ADC=180°﹣∠AEC=100°,
故答案为:100.
23.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 x<3 .
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
∵点A、B、C三点都在圆外,
∴x<3.
故答案为:x<3;
24.(2018秋?丰县期中)平面内有一点P到圆上最远的距离是6,最近的距离是2,则圆的半径是 2或4 .
【分析】分两种情况:点在圆外,直径等于两个距离的差;点在圆内,直径等于两个距离的和.
【解答】解:∵点P到⊙O的最近距离为2,最远距离为6,则:
当点在圆外时,则⊙O的直径为6﹣2=4,半径是2;
当点在圆内时,则⊙O的直径是6+2=8,半径为4,
综上,圆的半径是2或4,
故答案为:2或4.
25.(2018秋?镇江期中)已知⊙O的半径为3cm,OP=4cm,A是OP的中点,则点A与⊙O的位置关系是点A在 圆内 .(填圆内、圆外或圆上)
【分析】知道OP的长,点A是OP的中点,得到OA的长与半径的关系,求出点A与圆的位置关系.
【解答】解:因为OP=4cm,A是线段OP的中点,所以OA=2cm,小于圆的半径,因此点A在圆内.
故答案为:圆内.
26.(2017?宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 5 .
【分析】根据圆的确定先做出过A,B,C三点的外接圆,从而得出答案.
【解答】解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
27.(2018秋?石景山区期末)如图,⊙O是正方形ABCD的外接圆,若E是上一点,则∠DEC= 45 °.
【分析】连接OD、OC,如图,根据正方形的性质得到∠COD=90°,然后根据圆周角定理得到∠CED的度数.
【解答】解:连接OD、OC,如图,
∵⊙O是正方形ABCD的外接圆,
∴∠COD=90°,
∴∠COD=90°,
∴∠CED=∠COD=45°.
故答案为45.
28.(2018秋?丽江期末)已知一个三角形三边分别为13cm,12cm,5cm,则此三角形外接圆半径为 6.5 cm
【分析】首先得出三角形是直角三角形,再根据直角三角形的斜边为它的外接圆的直径得到这个三角形的外接圆的半径.
【解答】解:∵52+122=132,
∴此三角形是直角三角形,
因为直角三角形的斜边为它的外接圆的直径,
所以这个三角形的外接圆的半径是6.5cm.
故答案为:6.5.
29.(2018秋?潮南区期末)若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
【分析】首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
【解答】解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB===30°,
∵⊙O的半径为2,
∴OB=2,
∴BD=OB?cos∠OBD=2×cos30°=2×=,
∴BC=2BD=2.
∴等边△ABC的边长为2.
故答案为:2.
30.(2018秋?綦江区校级期中)如图,△ABC内接于⊙O,若∠OAB=30°,则∠C= 60° .
【分析】根据等腰三角形的性质,三角形内角和定理求出∠AOB,根据圆周角定理解答.
【解答】解:∵OA=OB,
∴∠OBA=∠OAB=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
由圆周角定理得,∠C=∠AOB=60°,
故答案为:60°.
31.(2018秋?西城区期末)如图,⊙O的半径是5,点A在⊙O上.P是⊙O所在平面内一点,且AP=2,过点P作直线l,使l⊥PA.
(1)点O到直线l距离的最大值为 7 ;
(2)若M,N是直线l与⊙O的公共点,则当线段MN的长度最大时,OP的长为 .
【分析】(1)如图1,当点P在圆外且O,A,P三点共线时,点O到直线l距离的最大,于是得到结论;
(2)如图2,根据已知条件得到线段MN是⊙O的直径,根据勾股定理即可得到结论.
【解答】解:(1)如图1,∵l⊥PA,
∴当点P在圆外且O,A,P三点共线时,点O到直线l距离的最大,
最大值为AO+AP=5+2=7;
(2)如图2,∵M,N是直线l与⊙O的公共点,当线段MN的长度最大时,
线段MN是⊙O的直径,
∵l⊥PA,
∴∠AOO=90°,
∵AP=2,OA=5,
∴OP==,
故答案为:7,.
32.(2017秋?江阴市期末)如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,连接MN,设直线y=x交MN于点G.若PG:PN=3:4,△PGN的周长为12,则△PON的周长是 16或18﹣2 .
【分析】根据圆周角定理得到∠MPN=90°,推出∠MOP=∠NOP=45°,得到PM=PN,设PG=3x,PN=4x,得到PM=4x,根据勾股定理得到MN=4x,根据相似三角形的性质得到PO=x,NG=2x+x或NG=2x﹣x,根据三角形的周长公式列方程3x+4x+2x+x=12或3x+4x+2x﹣x=12,求得x=或x=,当x=时,当x=时,根据三角形的周长公式得到结论.
【解答】解:∵∠MON=90°,
∴MN是直径,
∴∠MPN=90°,
∵直线y=x是∠MON的平分线,
∴∠MOP=∠NOP=45°,
∴=,
∴PM=PN,
∵PG:PN=3:4,
∴设PG=3x,PN=4x,
∴PM=4x,
∴MN=4x,
∵∠PNM=∠PON=45°,
∠NPG=∠OPN,
∴△PGN∽△PNO,
∴,
∴=,
∴PO=x,
∴OG=PO﹣PG=x,
∵∠OMN=∠NPO,
∴△OMG∽△NPG,
∴,
∴=,
∴NG=2x+x或NG=2x﹣x,
∵△PGN的周长为12,
∴3x+4x+2x+x=12或3x+4x+2x﹣x=12,
解得:x=或x=,
∴当x=时,PO=×,PN=4×,GN=(2+1)×,
∵△PGN∽△PNO,
∴==,
∴ON=×(2+1)×,
∴△PON的周长=PO+PN+ON=×+4×+×(2+1)×=16,
同理当x=时,△PON的周长=18﹣2.
综上所述,△PON的周长是16或18﹣2.
故答案为:16或18﹣2.
33.(2018?益阳)如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 45 度.
【分析】利用圆周角定理得到∠ADB=90°,再根据切线的性质得∠ABC=90°,然后根据等腰三角形的判定方法得到△ABC为等腰直角三角形,从而得到∠C的度数.
【解答】解:∵AB为直径,
∴∠ADB=90°,
∵BC为切线,
∴AB⊥BC,
∴∠ABC=90°,
∵AD=CD,
∴△ABC为等腰直角三角形,
∴∠C=45°.
故答案为45.
34.(2018?巴中)如图,在矩形ABCD中,以AD为直径的半圆与边BC相切于点E,若AD=4,则图中的阴影部分的面积为 8﹣2π .
【分析】由半圆的直径为4且与矩形一边BC相切可得矩形的宽AB=2,再根据阴影部分面积=矩形面积﹣半圆面积求解可得.
【解答】解:∵半圆的直径AD=4,且与BC相切,
∴半径为2,AB=2,
∴图中的阴影部分的面积为4×2﹣?π?22=8﹣2π,
故答案为:8﹣2π.
35.(2018?山西)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .
【分析】先利用勾股定理求出AB=10,进而求出CD=BD=5,再求出CF=4,进而求出DF=3,再判断出FG⊥BD,利用面积即可得出结论.
【解答】解:如图,
在Rt△ABC中,根据勾股定理得,AB=10,
∴点D是AB中点,
∴CD=BD=AB=5,
连接DF,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴BF=CF=BC=4,
∴DF==3,
连接OF,
∵OC=OD,CF=BF,
∴OF∥AB,
∴∠OFC=∠B,
∵FG是⊙O的切线,
∴∠OFG=90°,
∴∠OFC+∠BFG=90°,
∴∠BFG+∠B=90°,
∴FG⊥AB,
∴S△BDF=DF×BF=BD×FG,
∴FG===,
故答案为.
36.(2018?包头)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 115 度.
【分析】连接OC,根据切线的性质求出∠DCO,求出∠COB,即可求出答案.
【解答】解:
连接OC,
∵DC切⊙O于C,
∴∠DCO=90°,
∵∠D=40°,
∴∠COB=∠D+∠DCO=130°,
∴的度数是130°,
∴的度数是360°﹣130°=230°,
∴∠BEC==115°,
故答案为:115.
37.(2018?东莞市)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 π .(结果保留π)
【分析】连接OE,如图,利用切线的性质得OD=2,OE⊥BC,易得四边形OECD为正方形,先利用扇形面积公式,利用S正方形OECD﹣S扇形EOD计算由弧DE、线段EC、CD所围成的面积,然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积.
【解答】解:连接OE,如图,
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
易得四边形OECD为正方形,
∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣=4﹣π,
∴阴影部分的面积=×2×4﹣(4﹣π)=π.
故答案为π.
38.(2018?泰州)如图,△ABC中,∠ACB=90°,sinA=,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 或 .
【分析】分两种情形分别求解:如图1中,当⊙P与直线AC相切于点Q时,如图2中,当⊙P与AB相切于点T时,
【解答】解:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.
设PQ=PA′=r,
∵PQ∥CA′,
∴=,
∴=,
∴r=.
如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,
∵△A′BT∽△ABC,
∴=,
∴=,
∴A′T=,
∴r=A′T=.
综上所述,⊙P的半径为或.
39.(2018秋?如皋市期中)如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为 8 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=10,BC=B′C=8,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=5,继而求得CG=B′E=OH==4,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=10,BC=B′C=8,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=5,
∴B′H=OE=5,
∴CH=B′C﹣B′H=3,
∴CG=B′E=OH==4,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=8,
故答案为:8.
40.(2018秋?江都区期中)如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 4 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=6,BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=3,继而求得CG=B′E=OH==2,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=3,
∴B′H=OE=3,
∴CH=B′C﹣B′H=1,
∴CG=B′E=OH==2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
41.(2018?南京)如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C
旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点
F,则CF的长为 4 .
【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=5、BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=2.5,继而求得CG=B′E=OH===2,根据垂径定理可得CF的长.
【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,
∴B′H=OE=2.5,
∴CH=B′C﹣B′H=1.5,
∴CG=B′E=OH===2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
42.(2018秋?伊通县期末)如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为 110° .
【分析】根据三角形的内心的概念得到∠OBC=∠ABC=30°,∠OCB=∠ACB=40°,根据三角形内角和定理计算即可.
【解答】解:∵⊙O是△ABC的内切圆,
∴∠OBC=∠ABC=30°,∠OCB=∠ACB=40°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=110°,
故答案为:110°.
43.(2018秋?临洮县期末)如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 16cm .
【分析】根据切线的性质,得到直角三角形OAP,根据勾股定理求得PA的长;根据切线长定理,得BD=CD,CE=AE,PA=PB,从而求解.
【解答】解:连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
在直角三角形OAP中,根据勾股定理,得AP=8,
∴△PDE的周长为2AP=16.
故选答案为16cm.
44.(2018秋?长春期末)如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= 30° .
【分析】连接OB,AD,BD,由多边形是正六边形可求出∠AOB的度数,再根据圆周角定理即可求出∠ADB的度数,利用弦切角定理求出∠PAB即可.
【解答】解:连接OB,AD,BD,
∵多边形ABCDEF是正多边形,
∴AD为外接圆的直径,
∠AOB==60°,
∴∠ADB=∠AOB=×60°=30°.
∵直线PA与⊙O相切于点A,
∴∠PAB=∠ADB=30°.
故答案为:30°.
45.(2017秋?仙居县期末)已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是 4﹣2 .
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于4﹣2小于等于4,由此即可判断.
【解答】解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于4﹣2小于等于4,
∴B,M之间距离的最小值是4﹣2.
故答案为:4﹣2.
46.(2018?郴州)如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为 12π cm.(结果用π表示)
【分析】根据圆锥的展开图为扇形,结合圆周长公式的求解.
【解答】解:设底面圆的半径为rcm,
由勾股定理得:r==6,
∴2πr=2π×6=12π,
故答案为:12π.
47.(2018?盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
【分析】先根据图1确定:图2的周长=2个的长,根据弧长公式可得结论.
【解答】解:由图1得:的长+的长=的长
∵半径OA=2cm,∠AOB=120°
则图2的周长为:=
故答案为:.
48.(2018?永州)如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则的长为 .
【分析】由点A(1,1),可得OA==,点A在第一象限的角平分线上,那么∠AOB=45°,再根据弧长公式计算即可.
【解答】解:∵点A(1,1),
∴OA==,点A在第一象限的角平分线上,
∵以点O为旋转中心,将点A逆时针旋转到点B的位置,
∴∠AOB=45°,
∴的长为=.
故答案为.
49.(2018秋?庆阳期末)如图,在△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=2,则扇形BDE的面积为 .
【分析】根据三角形内角和定理求出∠C,根据三角形的外角的性质求出∠BDE,根据扇形面积公式计算.
【解答】解:∵∠A=60°,∠B=100°,
∴∠C=20°,
∵BD=DC=1,DE=DB,
∴DE=DC=1,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积==,
故答案为:.
50.(2018春?郓城县期中)在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是 12π cm2.
【分析】直接利用扇形面积公式代入求出面积即可.
【解答】解:∵在圆心角为120°的扇形AOB中,半径OA=6cm,
∴扇形OAB的面积是:=12π(cm2),
故答案为12π.
