(苏教版)2018年高中数学第3章空间向量与立体几何3.2.2空间线面关系的判定课件1选修2-1(27张PPT)
文档属性
| 名称 | (苏教版)2018年高中数学第3章空间向量与立体几何3.2.2空间线面关系的判定课件1选修2-1(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 452.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-31 15:11:10 | ||
图片预览


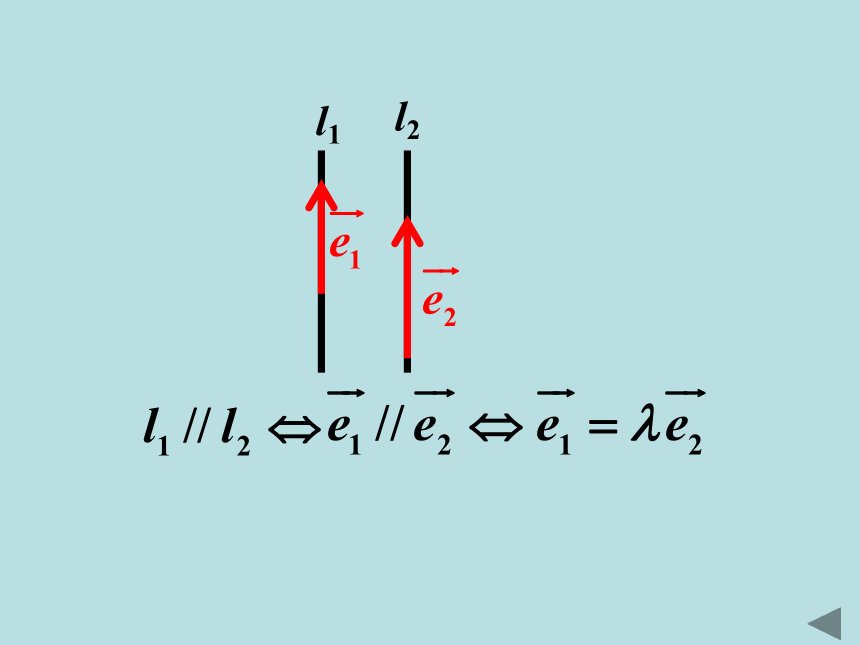
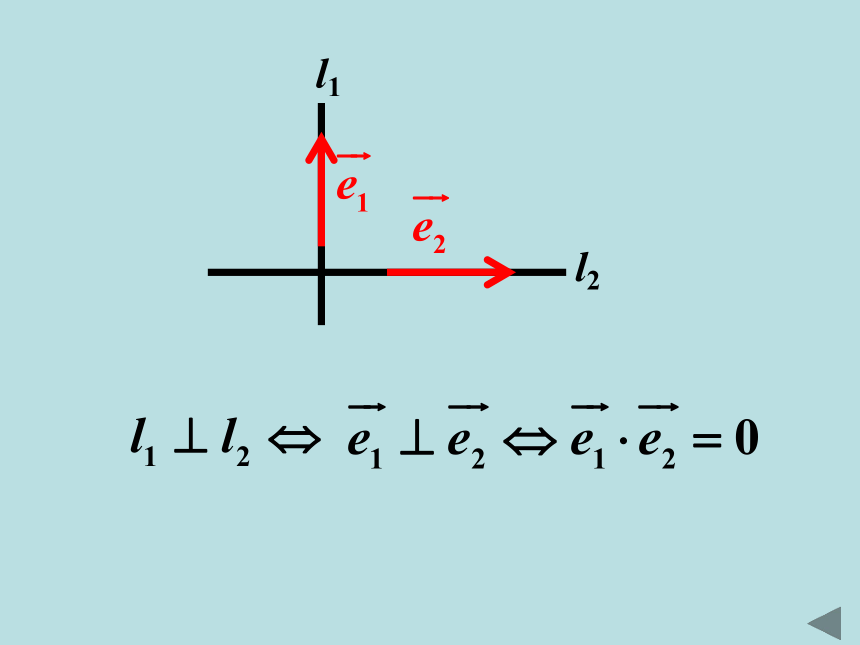
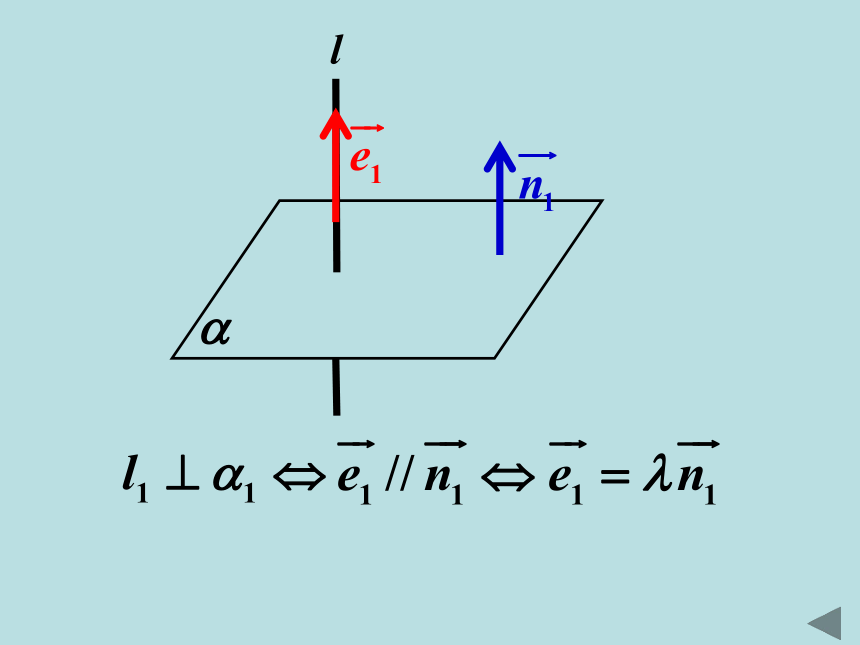
文档简介
课件27张PPT。空间线面关系的判定温故知新:
1、非零向量 , 的充要条件是 2、设向量 的夹角为 ,则3、共面向量定理 如果两个向量 不共线,那么
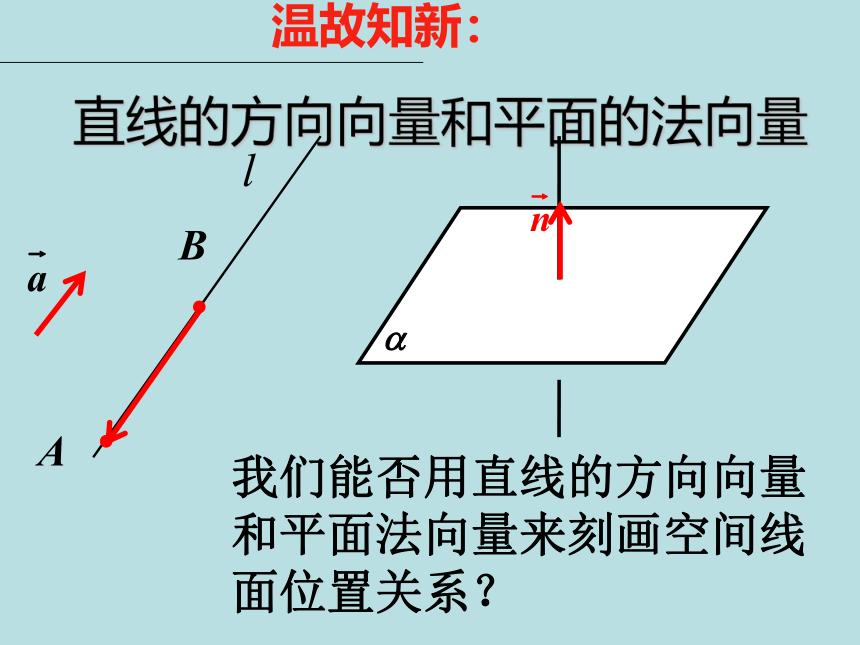
向量 与向量 共面的充要条件是存在有序实数组,使得:直线的方向向量和平面的法向量温故知新: 我们能否用直线的方向向量和平面法向量来刻画空间线面位置关系?l1l2l1l2l1l 设空间两条直线 的方向向量为
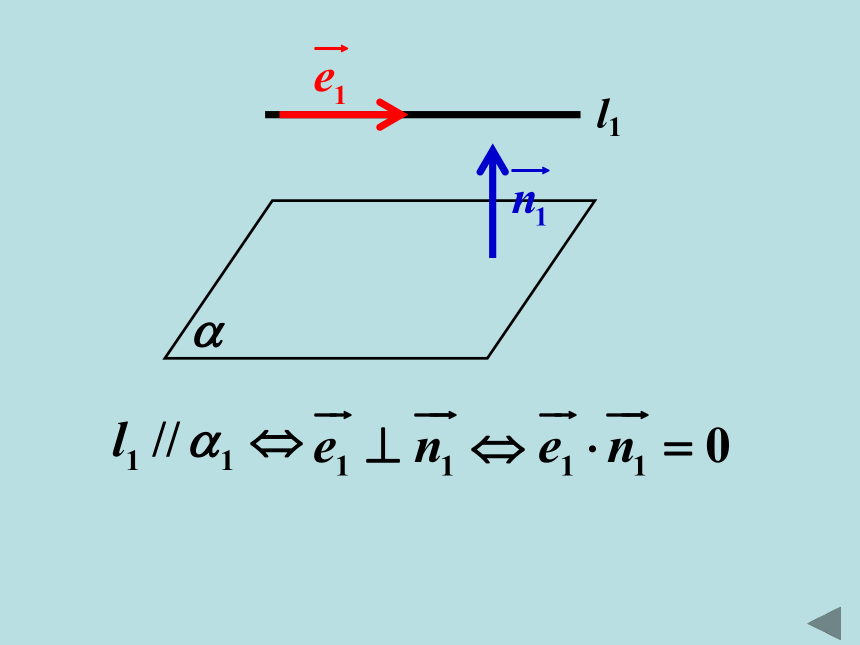
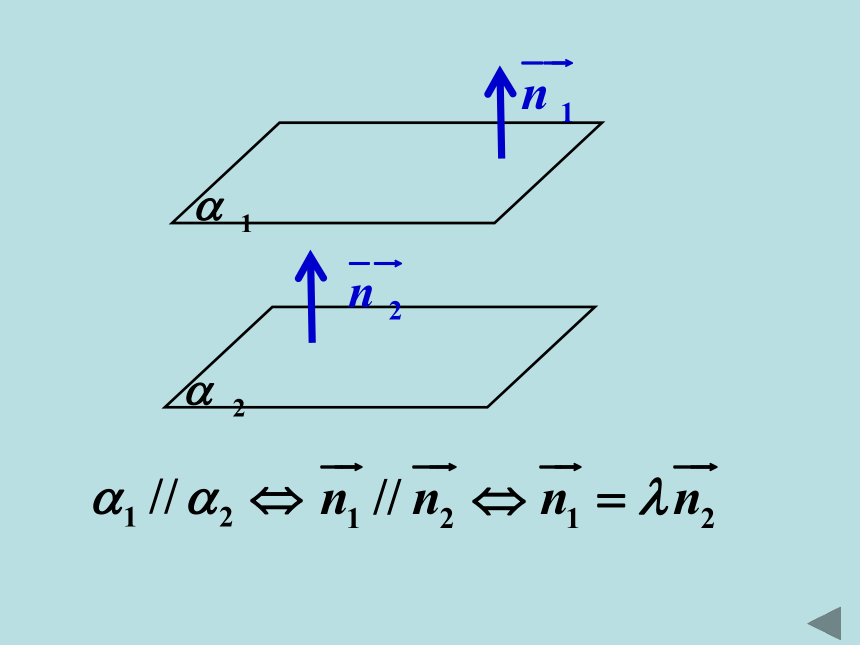
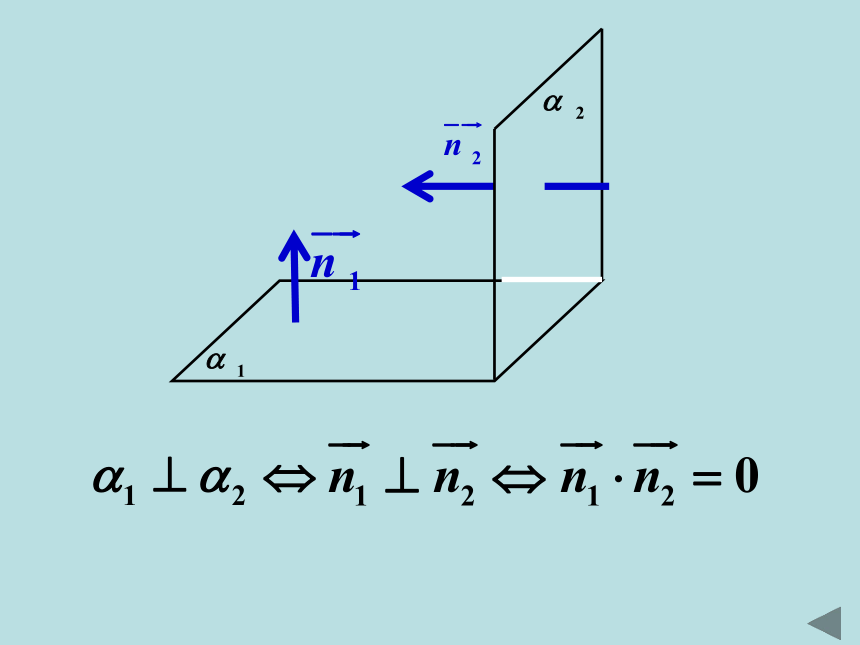
两个平面 的法向量分别为例题1 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直. 如图, 是平面 的一条斜线, 为斜足, , 为垂足, ,且
求证:
OBDCA问题探究三垂线定理 在平面内的一条直线,如果它
和这个平面的一条斜线的射影垂直,那么
它也和这条斜线垂直.变式练习:
写出三垂线定理的逆定理,并用向量的方法加以证明.三垂线定理 在平面内的一条直线,如果它
和这个平面的一条斜线的射影垂直,那么
它也和这条斜线垂直.三垂线定理的逆定理 在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.例2、证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面。(直线与平面垂直的判定定理)已知:如图,
求证:
分析:要证明直线与平面垂直,只要证明该直线垂直于平面内任意一条直线。相交不共线又共面存在有序实数组使得,例3、如图,在直三棱柱 - 中,
是棱 的中点,
求证:
证明:在直三棱柱 - 中,
因为 ,所以
因为 ,而
所以 ,所以
在 中,因为
所以所以
因为 , ,
且 是棱 中点,所以 ,
所以所以:所以:
即, 思考:还有其它的证明方法吗?
利用相似形与线面垂直分析:连结 交 于点
因为
所以,要证
就是证
即证
1、利用 相似可以证明 ,
从而2、利用 知道 ,即 你能试着建立适当的空间直角坐标系,用坐标表示向量,再证明它们互相垂直吗?证明:分别以
所在直线为 轴, 轴, 轴,建
立空间直角坐标系图中相应点的坐标为:所以:所以:即,三种方法的比较:
证法一是几何向量法,要熟练掌握向量的加减运算及所满足的运算律。
证法二是向量的坐标运算法,关键是要恰当地建立空间直角坐标系,探求出各点的坐标。
证法三是几何向量法和立体几何法的综合运用。 最终都是应用向量的数量积为0来证明线线垂直。证明:设正方体棱长为1, 为单位正交
基底,建立如图所示坐标系D-xyz,则可得:所以课堂小结: 本节课主要研究了用向量的方法判定空间线线、线面垂直关系。
如果要判定两条直线 垂直 ,可以通过证明它们的方向向量 , 的数量积为0实现谢谢指导
1、非零向量 , 的充要条件是 2、设向量 的夹角为 ,则3、共面向量定理 如果两个向量 不共线,那么
向量 与向量 共面的充要条件是存在有序实数组,使得:直线的方向向量和平面的法向量温故知新: 我们能否用直线的方向向量和平面法向量来刻画空间线面位置关系?l1l2l1l2l1l 设空间两条直线 的方向向量为
两个平面 的法向量分别为例题1 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直. 如图, 是平面 的一条斜线, 为斜足, , 为垂足, ,且
求证:
OBDCA问题探究三垂线定理 在平面内的一条直线,如果它
和这个平面的一条斜线的射影垂直,那么
它也和这条斜线垂直.变式练习:
写出三垂线定理的逆定理,并用向量的方法加以证明.三垂线定理 在平面内的一条直线,如果它
和这个平面的一条斜线的射影垂直,那么
它也和这条斜线垂直.三垂线定理的逆定理 在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.例2、证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面。(直线与平面垂直的判定定理)已知:如图,
求证:
分析:要证明直线与平面垂直,只要证明该直线垂直于平面内任意一条直线。相交不共线又共面存在有序实数组使得,例3、如图,在直三棱柱 - 中,
是棱 的中点,
求证:
证明:在直三棱柱 - 中,
因为 ,所以
因为 ,而
所以 ,所以
在 中,因为
所以所以
因为 , ,
且 是棱 中点,所以 ,
所以所以:所以:
即, 思考:还有其它的证明方法吗?
利用相似形与线面垂直分析:连结 交 于点
因为
所以,要证
就是证
即证
1、利用 相似可以证明 ,
从而2、利用 知道 ,即 你能试着建立适当的空间直角坐标系,用坐标表示向量,再证明它们互相垂直吗?证明:分别以
所在直线为 轴, 轴, 轴,建
立空间直角坐标系图中相应点的坐标为:所以:所以:即,三种方法的比较:
证法一是几何向量法,要熟练掌握向量的加减运算及所满足的运算律。
证法二是向量的坐标运算法,关键是要恰当地建立空间直角坐标系,探求出各点的坐标。
证法三是几何向量法和立体几何法的综合运用。 最终都是应用向量的数量积为0来证明线线垂直。证明:设正方体棱长为1, 为单位正交
基底,建立如图所示坐标系D-xyz,则可得:所以课堂小结: 本节课主要研究了用向量的方法判定空间线线、线面垂直关系。
如果要判定两条直线 垂直 ,可以通过证明它们的方向向量 , 的数量积为0实现谢谢指导
