高中数学人教B版选修2-2 1.4.1曲边梯形的面积与定积分 课件(43张)
文档属性
| 名称 | 高中数学人教B版选修2-2 1.4.1曲边梯形的面积与定积分 课件(43张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-31 15:14:10 | ||
图片预览







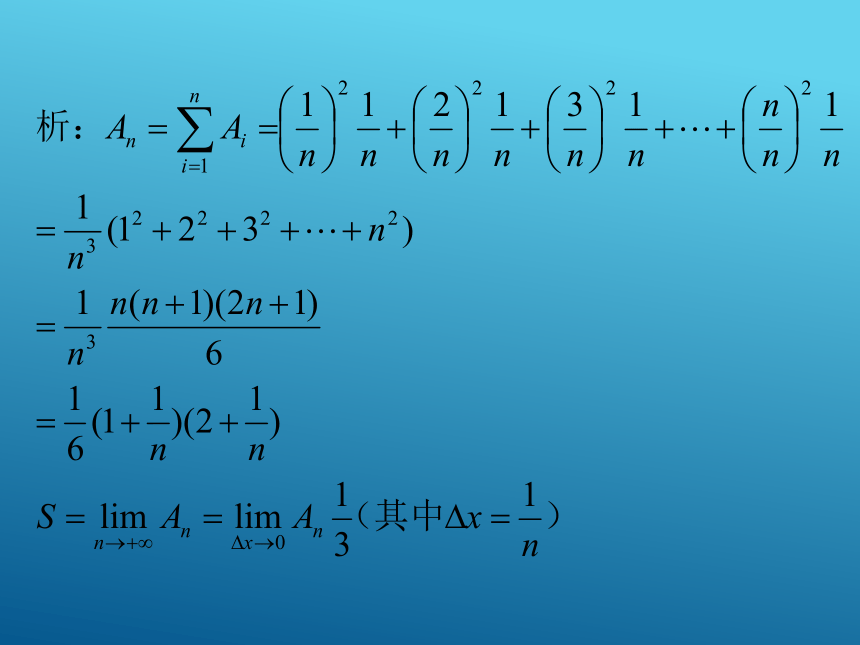

文档简介
课件43张PPT。人教B选修2-2第一章第四节第一课时 曲边梯形面积与定积分教学目标:
(1)体会“无限分割思想”求曲边梯形的面积
(2)理解定积分的概念以及它的几何意义;
重点:定积分的概念以及它的几何意义;
难点:如何把曲线围成区域的面积转化成矩形面积的和。微积分简单粗暴版定义 微分:无限细分,以至于每一份
都无限微小 积分:把微小的积累为一个大的
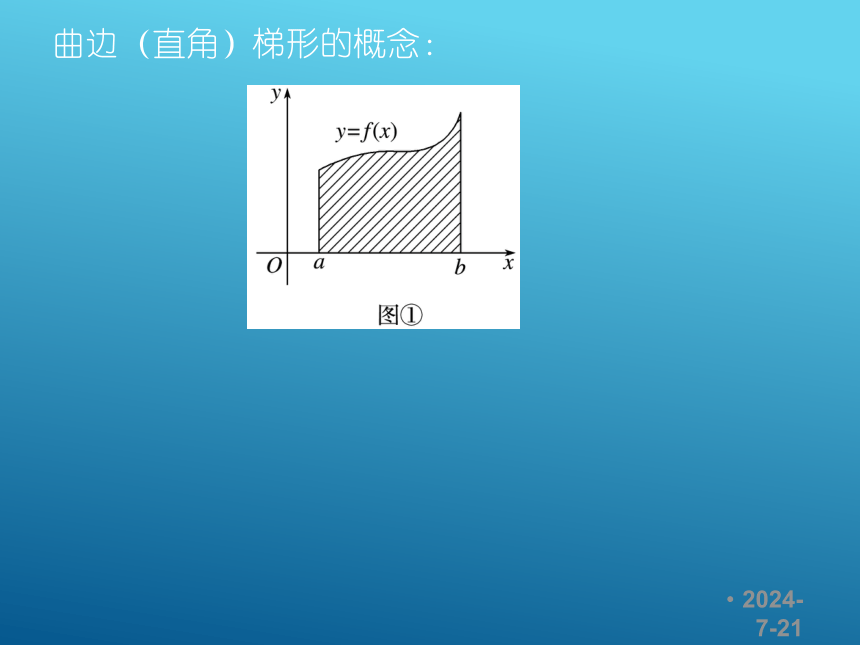
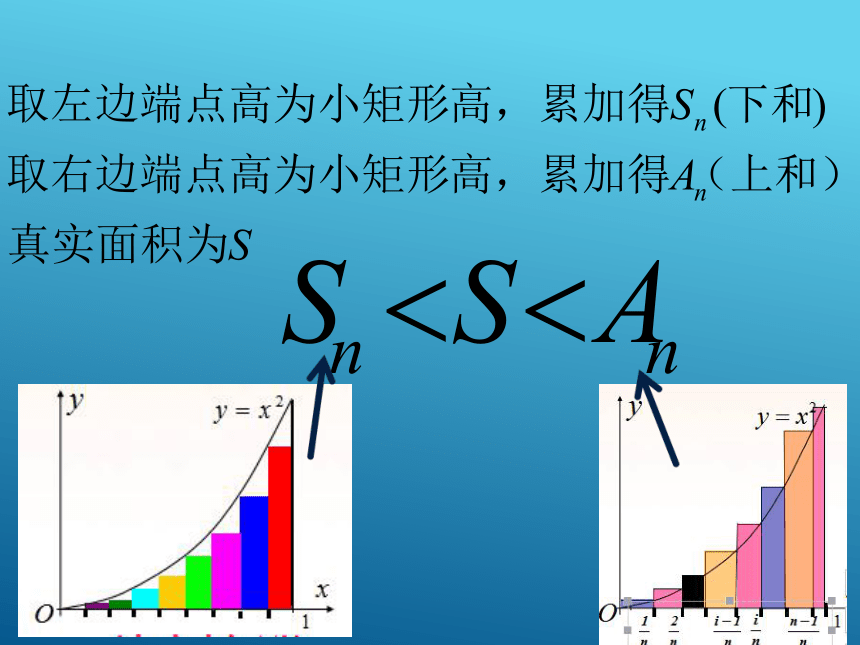
微积分的基础理论:极限思想 三国时期的刘徽(约公元225年—295年),形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。“割圆术”,是以“圆内接正多边形的面积”, 来无限逼近“圆面积”。 前面学习的导数是微分的一部分 今天我们开始学习积分的初步:定积分定积分的实际背景曲边(直角)梯形的概念:2019/1/31 例1、求由曲线y=x2和直线x=1,y=0围成的图形面积.教材上统一取了每个区间左端点的高度作为每个矩形的高,现在同学们再试一下取右边端点的高度作为每个矩形的高,所有这些小矩形的面积和记为An,再研究 时,An是否还是趋近于曲边三角形的面积?
定积分的实际背景1
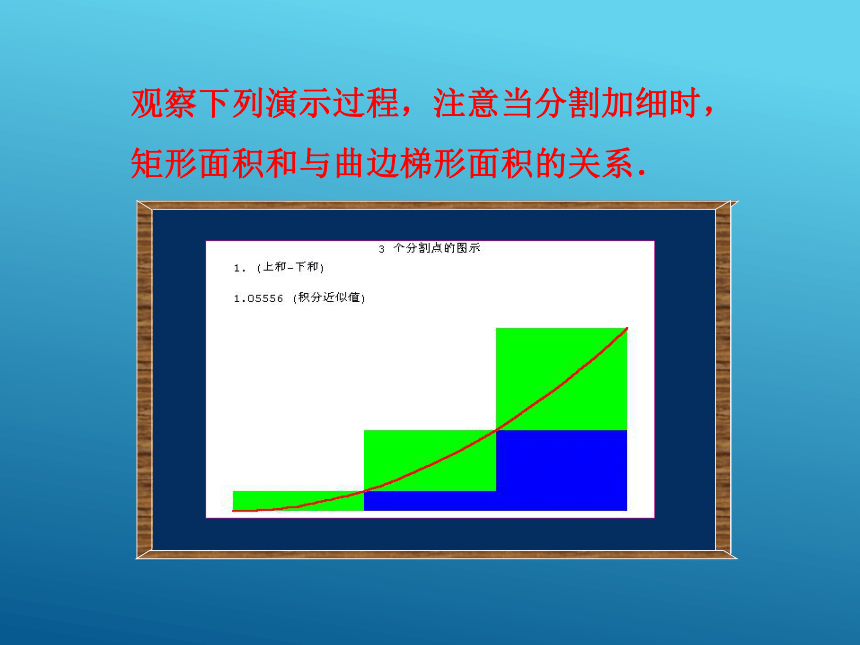
曲边梯形面积观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.当区间无穷小时,区间上函数值
几乎一样,所以取小区间内哪个点
的高: 为小矩形的高都可以。例2、某物体做自由落体运动
速度v=10t,求2秒内物体运动路程 定积分的实际背景3
变速直线运动的路程 定积分的实际背景2
变力做功思考:求曲边梯形的面积,求变力做功,求变速直线运动的路程的步骤,它们有什么共同点?
三个问题均可通过“分割、近似代替、求和、取极限”解决.
都可以归结为一个特定形式和的极限
牛顿等数学教得到了解决这一类问题的一般方法:
求函数定积分定积分的概念.积分上限用定积分改写例1的结果为: 用定积分改写例3的结果为: 利用定义求定积分步骤:牛刀小试2019/1/312019/1/312019/1/31 本节重点内容:定积分的几何意义思考1:1、2、把下面的面积写成定积分的形式:如果被积函数是负的,函数曲线在x轴之下,定积分的值与曲边梯形的面积的关系是什么?思考2:总结:思考3:0利用积分的几意义求定积分当堂检测:
(1)体会“无限分割思想”求曲边梯形的面积
(2)理解定积分的概念以及它的几何意义;
重点:定积分的概念以及它的几何意义;
难点:如何把曲线围成区域的面积转化成矩形面积的和。微积分简单粗暴版定义 微分:无限细分,以至于每一份
都无限微小 积分:把微小的积累为一个大的
微积分的基础理论:极限思想 三国时期的刘徽(约公元225年—295年),形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。“割圆术”,是以“圆内接正多边形的面积”, 来无限逼近“圆面积”。 前面学习的导数是微分的一部分 今天我们开始学习积分的初步:定积分定积分的实际背景曲边(直角)梯形的概念:2019/1/31 例1、求由曲线y=x2和直线x=1,y=0围成的图形面积.教材上统一取了每个区间左端点的高度作为每个矩形的高,现在同学们再试一下取右边端点的高度作为每个矩形的高,所有这些小矩形的面积和记为An,再研究 时,An是否还是趋近于曲边三角形的面积?
定积分的实际背景1
曲边梯形面积观察下列演示过程,注意当分割加细时,
矩形面积和与曲边梯形面积的关系.当区间无穷小时,区间上函数值
几乎一样,所以取小区间内哪个点
的高: 为小矩形的高都可以。例2、某物体做自由落体运动
速度v=10t,求2秒内物体运动路程 定积分的实际背景3
变速直线运动的路程 定积分的实际背景2
变力做功思考:求曲边梯形的面积,求变力做功,求变速直线运动的路程的步骤,它们有什么共同点?
三个问题均可通过“分割、近似代替、求和、取极限”解决.
都可以归结为一个特定形式和的极限
牛顿等数学教得到了解决这一类问题的一般方法:
求函数定积分定积分的概念.积分上限用定积分改写例1的结果为: 用定积分改写例3的结果为: 利用定义求定积分步骤:牛刀小试2019/1/312019/1/312019/1/31 本节重点内容:定积分的几何意义思考1:1、2、把下面的面积写成定积分的形式:如果被积函数是负的,函数曲线在x轴之下,定积分的值与曲边梯形的面积的关系是什么?思考2:总结:思考3:0利用积分的几意义求定积分当堂检测:
