北师大八年级下册《1.3线段的垂直平分线》同步练习(含答案)
文档属性
| 名称 | 北师大八年级下册《1.3线段的垂直平分线》同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 203.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 11:56:55 | ||
图片预览


文档简介
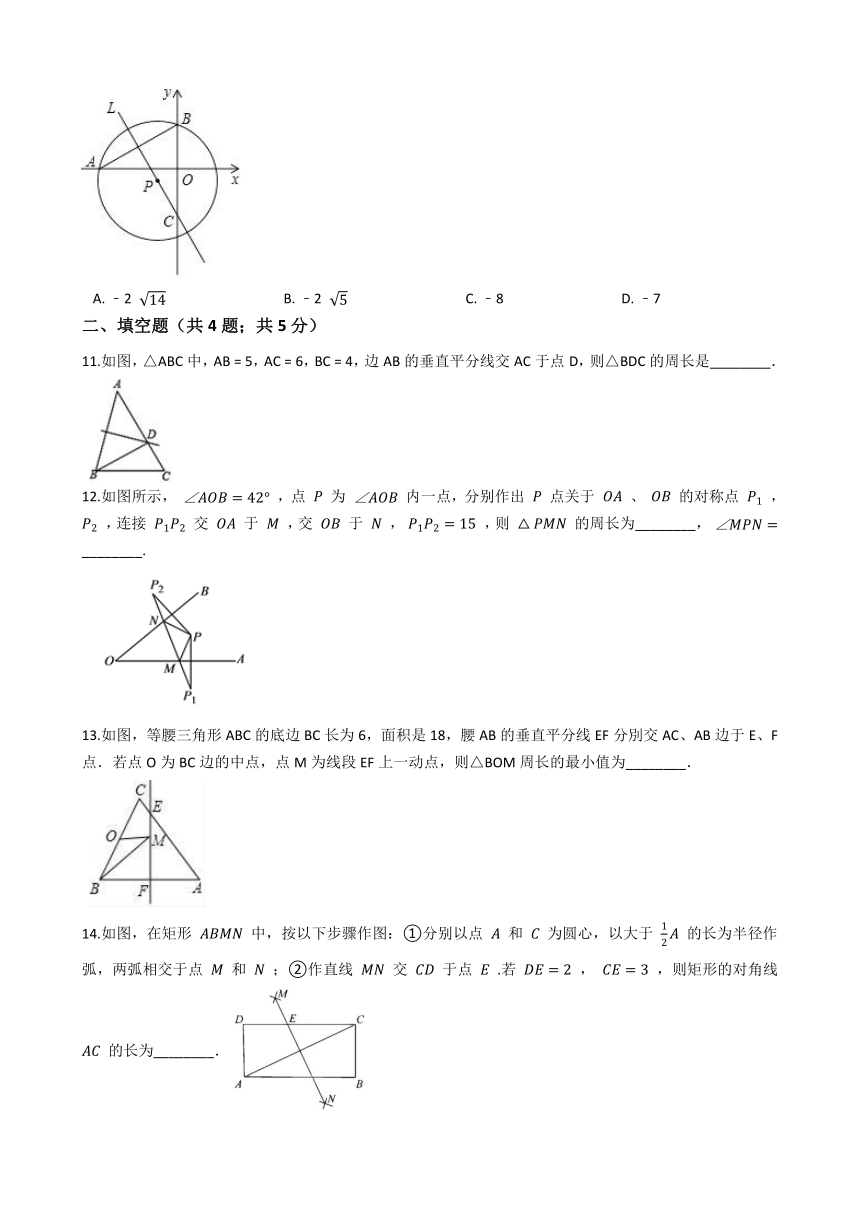
北师大版八年级数学下册1.3 线段的垂直平分线 同步练习
一、单选题(共10题;共20分)
1.如图,在△ABC中,分别以点A和点B为圆心,大于
1
2
AB长为半径画弧,两弧分别相交于点M,N,作直线MN,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为(? ?) /
A.27 B.14 C.17 D.20
2.在 ????△?????? 中,∠ACB=90°,斜边 ???? 的中垂线 ???? 分别交BC,AB于点D,E.已知BD=5,CD=3,则AC的长为(??? )
/
A.8 B.4 C./ D.2
3.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是(?? )
/
A.1对 B.2对 C.3对 D.4对
4.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中正确的是(????? )
/
A./B./C./D./
5.如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则( ??)
/
A.BE+CF>EF B.BE+CF=EF C.BE+CF<EF D.BE+CF与EF的大小关 系不能确定.
6.联欢会上,A,B,C三名选手站在一个三角形三个顶点上玩抢凳子游戏,在他们中间放个木凳,谁先抢到凳子就获胜,为使游戏公平,凳子应放的最适当位置是△ABC的 (????? )
A.?三边中线的交点??????????/B.?三边中垂线的交点??????????/C.?三条角平分线的交点??????????/D.?三边上高的交点
7.在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( ??) /
A.?5cm????????????????????????????????????/B.?6cm????????????????????????????????????/C.?7 cm????????????????????????????????????/D.?8 cm
8.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( ??)
/
A.AB>AC=CE B.AB=AC>CE C.AB>AC>CE D.AB=AC=CE 9.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于
1
2
BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为(??? ) /
A.?5???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
10.如图,坐标平面上,A,B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A,B,C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?(?? )
/
A.?﹣2
14
??????????????????????????????????/B.?﹣2
5
??????????????????????????????????/C.?﹣8??????????????????????????????????/D.?﹣7
二、填空题(共4题;共5分)
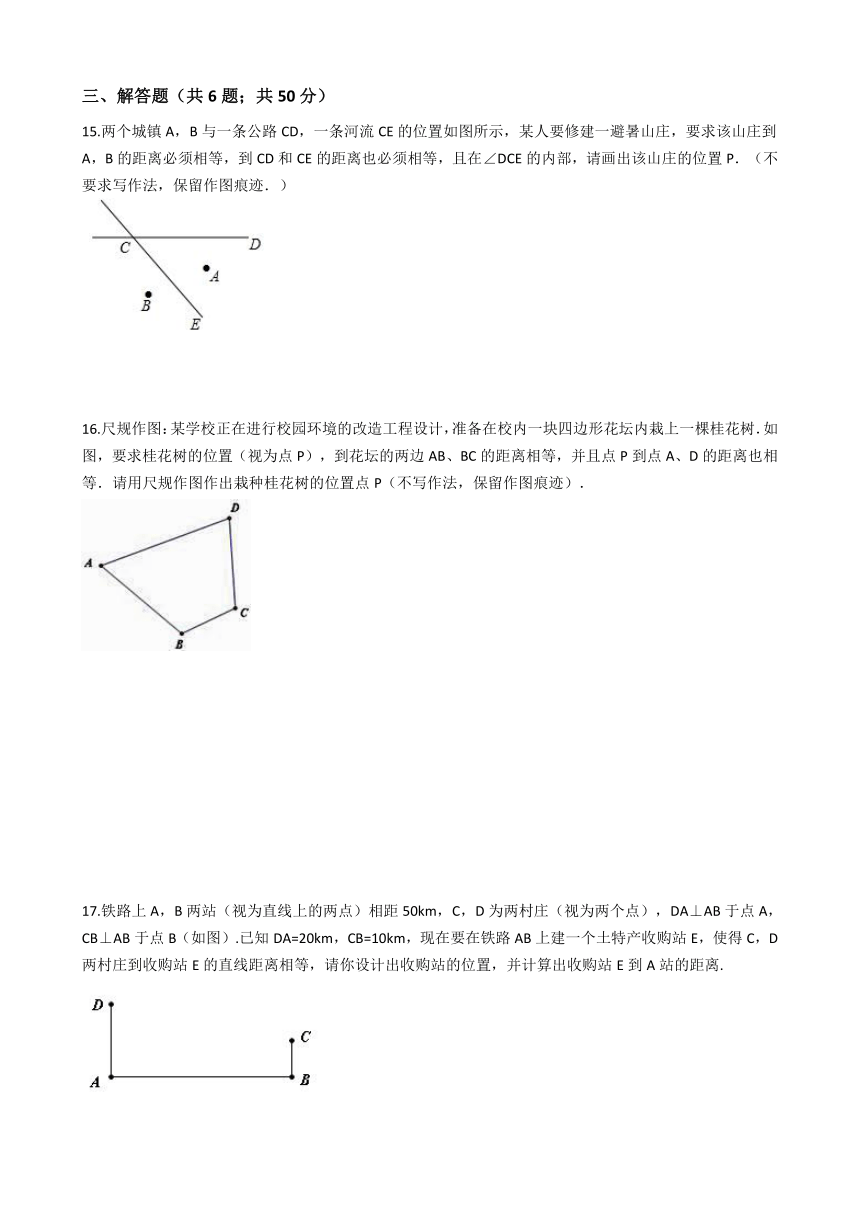
11.如图,△ABC中,AB = 5,AC = 6,BC = 4,边AB的垂直平分线交AC于点D,则△BDC的周长是________.
12.如图所示, ∠??????=42° ,点 ?? 为 ∠?????? 内一点,分别作出 ?? 点关于 ???? 、 ???? 的对称点
??
1
,
??
2
,连接
??
1
??
2
交 ???? 于 ?? ,交 ???? 于 ?? ,
??
1
??
2
=15 ,则 △?????? 的周长为________, ∠??????= ________.
/
13.如图,等腰三角形ABC的底边BC长为6,面积是18,腰AB的垂直平分线EF分別交AC、AB边于E、F点.若点O为BC边的中点,点M为线段EF上一动点,则△BOM周长的最小值为________.
/
14.如图,在矩形 ???????? 中,按以下步骤作图:①分别以点 ?? 和 ?? 为圆心,以大于
1
2
?? 的长为半径作弧,两弧相交于点 ?? 和 ?? ;②作直线 ???? 交 ???? 于点 ?? .若 ????=2 , ????=3 ,则矩形的对角线 ???? 的长为________./
三、解答题(共6题;共50分)
15.两个城镇A,B与一条公路CD,一条河流CE的位置如图所示,某人要修建一避暑山庄,要求该山庄到A,B的距离必须相等,到CD和CE的距离也必须相等,且在∠DCE的内部,请画出该山庄的位置P.(不要求写作法,保留作图痕迹.)
/
16.尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).
/
17.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离.
/
18.如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): /
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
19.如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
/
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.
20.如图,AD是△ABC的角平分线,EF是AD的垂直平分线. 求证:/
(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】10
12.【答案】15;96°
13.【答案】9
14.【答案】/
三、解答题
15.【答案】解:作法:①作∠ECD的平分线CF,
②作线段AB的中垂线MN,
③MN与CF交于点P,则P就是山庄的位置.
/
16.【答案】解:(1)①分别以A、D为圆心,以大于
1
2
AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
( 2 )①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于
1
2
GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
③BI与EF相交于点P,则点P即为所求点.
/
17.【答案】解:
/
连接DE,CE,设AE=x km,则BE=(50-x) km ,
在Rt△ADE中, ??
??
2
=??
??
2
+??
??
2
,
∴
DE
2
=
20
2
+
??
2
在Rt△BCE中, ??
??
2
=??
??
2
+??
??
2
?, ∴CE2=102+(50-x)2 ,
又DE=CE,
∴202+x2=102+(50-x)2 , 解得x=22 ∴收购站E到A站的距离为22km。
18.【答案】(1)解:如图,作AB的垂直平分线,交BC于点P,则点P即为所求; / (2)解:如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB, / 连接EC,③作EC的垂直平分线交BC于点F; ∴Rt△DEF即为所求
19.【答案】(1)解:∵DE是AB的垂直平分线,GF是AC的垂直平分线, ∴EB=EA,GA=GC.
∵BC=BE+EG+GC, ∴BC=AE+EG+AG=△AEG的周长=10
(2)解:∵∠BAC=128°, ∴∠B+∠C=180°-∠BAC=180°-128°=52°.
∵EB=EA,GA=GC, ∴∠BAE=∠B,∠GAC=∠C, ∴∠EAG=∠BAC-∠BAE-∠GAC=∠BAC-(∠B+∠C)=128°-52°=76°
20.【答案】(1)证明:连接AE / ∵EF是AD的垂直平分线,∴AE=DE, ∴∠EAD=∠EDA; (2)证明:∵EF是AD的垂直平分线,∴AF=DF, ∴∠BAD=∠ADF, ∵AD是△ABC的角平分线, ∴∠BAD=∠CAD, ∴∠ADF=∠CAD, ∴DF∥AC; (3)证明:由(1)∠EAD=∠EDA,即∠ADE=∠CAD+∠EAC,∵∠ADE=∠BAD+∠B,∠BAD=∠CAD, ∴∠EAC=∠B.
一、单选题(共10题;共20分)
1.如图,在△ABC中,分别以点A和点B为圆心,大于
1
2
AB长为半径画弧,两弧分别相交于点M,N,作直线MN,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为(? ?) /
A.27 B.14 C.17 D.20
2.在 ????△?????? 中,∠ACB=90°,斜边 ???? 的中垂线 ???? 分别交BC,AB于点D,E.已知BD=5,CD=3,则AC的长为(??? )
/
A.8 B.4 C./ D.2
3.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是(?? )
/
A.1对 B.2对 C.3对 D.4对
4.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中正确的是(????? )
/
A./B./C./D./
5.如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则( ??)
/
A.BE+CF>EF B.BE+CF=EF C.BE+CF<EF D.BE+CF与EF的大小关 系不能确定.
6.联欢会上,A,B,C三名选手站在一个三角形三个顶点上玩抢凳子游戏,在他们中间放个木凳,谁先抢到凳子就获胜,为使游戏公平,凳子应放的最适当位置是△ABC的 (????? )
A.?三边中线的交点??????????/B.?三边中垂线的交点??????????/C.?三条角平分线的交点??????????/D.?三边上高的交点
7.在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( ??) /
A.?5cm????????????????????????????????????/B.?6cm????????????????????????????????????/C.?7 cm????????????????????????????????????/D.?8 cm
8.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( ??)
/
A.AB>AC=CE B.AB=AC>CE C.AB>AC>CE D.AB=AC=CE 9.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于
1
2
BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为(??? ) /
A.?5???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?7???????????????????????????????????????????/D.?8
10.如图,坐标平面上,A,B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A,B,C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?(?? )
/
A.?﹣2
14
??????????????????????????????????/B.?﹣2
5
??????????????????????????????????/C.?﹣8??????????????????????????????????/D.?﹣7
二、填空题(共4题;共5分)
11.如图,△ABC中,AB = 5,AC = 6,BC = 4,边AB的垂直平分线交AC于点D,则△BDC的周长是________.
12.如图所示, ∠??????=42° ,点 ?? 为 ∠?????? 内一点,分别作出 ?? 点关于 ???? 、 ???? 的对称点
??
1
,
??
2
,连接
??
1
??
2
交 ???? 于 ?? ,交 ???? 于 ?? ,
??
1
??
2
=15 ,则 △?????? 的周长为________, ∠??????= ________.
/
13.如图,等腰三角形ABC的底边BC长为6,面积是18,腰AB的垂直平分线EF分別交AC、AB边于E、F点.若点O为BC边的中点,点M为线段EF上一动点,则△BOM周长的最小值为________.
/
14.如图,在矩形 ???????? 中,按以下步骤作图:①分别以点 ?? 和 ?? 为圆心,以大于
1
2
?? 的长为半径作弧,两弧相交于点 ?? 和 ?? ;②作直线 ???? 交 ???? 于点 ?? .若 ????=2 , ????=3 ,则矩形的对角线 ???? 的长为________./
三、解答题(共6题;共50分)
15.两个城镇A,B与一条公路CD,一条河流CE的位置如图所示,某人要修建一避暑山庄,要求该山庄到A,B的距离必须相等,到CD和CE的距离也必须相等,且在∠DCE的内部,请画出该山庄的位置P.(不要求写作法,保留作图痕迹.)
/
16.尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).
/
17.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离.
/
18.如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): /
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
19.如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
/
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.
20.如图,AD是△ABC的角平分线,EF是AD的垂直平分线. 求证:/
(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】10
12.【答案】15;96°
13.【答案】9
14.【答案】/
三、解答题
15.【答案】解:作法:①作∠ECD的平分线CF,
②作线段AB的中垂线MN,
③MN与CF交于点P,则P就是山庄的位置.
/
16.【答案】解:(1)①分别以A、D为圆心,以大于
1
2
AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
( 2 )①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于
1
2
GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
③BI与EF相交于点P,则点P即为所求点.
/
17.【答案】解:
/
连接DE,CE,设AE=x km,则BE=(50-x) km ,
在Rt△ADE中, ??
??
2
=??
??
2
+??
??
2
,
∴
DE
2
=
20
2
+
??
2
在Rt△BCE中, ??
??
2
=??
??
2
+??
??
2
?, ∴CE2=102+(50-x)2 ,
又DE=CE,
∴202+x2=102+(50-x)2 , 解得x=22 ∴收购站E到A站的距离为22km。
18.【答案】(1)解:如图,作AB的垂直平分线,交BC于点P,则点P即为所求; / (2)解:如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB, / 连接EC,③作EC的垂直平分线交BC于点F; ∴Rt△DEF即为所求
19.【答案】(1)解:∵DE是AB的垂直平分线,GF是AC的垂直平分线, ∴EB=EA,GA=GC.
∵BC=BE+EG+GC, ∴BC=AE+EG+AG=△AEG的周长=10
(2)解:∵∠BAC=128°, ∴∠B+∠C=180°-∠BAC=180°-128°=52°.
∵EB=EA,GA=GC, ∴∠BAE=∠B,∠GAC=∠C, ∴∠EAG=∠BAC-∠BAE-∠GAC=∠BAC-(∠B+∠C)=128°-52°=76°
20.【答案】(1)证明:连接AE / ∵EF是AD的垂直平分线,∴AE=DE, ∴∠EAD=∠EDA; (2)证明:∵EF是AD的垂直平分线,∴AF=DF, ∴∠BAD=∠ADF, ∵AD是△ABC的角平分线, ∴∠BAD=∠CAD, ∴∠ADF=∠CAD, ∴DF∥AC; (3)证明:由(1)∠EAD=∠EDA,即∠ADE=∠CAD+∠EAC,∵∠ADE=∠BAD+∠B,∠BAD=∠CAD, ∴∠EAC=∠B.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
