北师大版八年级数学下册《1.4角平分线》同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学下册《1.4角平分线》同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 00:00:00 | ||
图片预览


文档简介
北师大版八年级数学下册1.4 角平分线 同步练习
一、单选题(共10题;共20分)
1.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B。下列结论中不一定成立的是(? )
/
A.PA=PB B.PO平分∠AOB C.OA=OB D.AB垂直平分OP
2.如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3cm,则AB与CD之间的距离为(?? ????)
/
A.3 cm B.6 cm C.9 cm D.无法确定
3.如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C,D为圆心,大于
1
2
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是(??? )
/
A.?△OCD是等腰三角形???????????????????????????????????????????/B.?点E到OA,OB的距离相等 C.?CD垂直平分OE???????????????????????????????????????????????????D.?证明射线OE是角平分线的依据是SSS
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90+
1
2
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则
??
△??????
=mn.其中正确的结论有(??? )
/
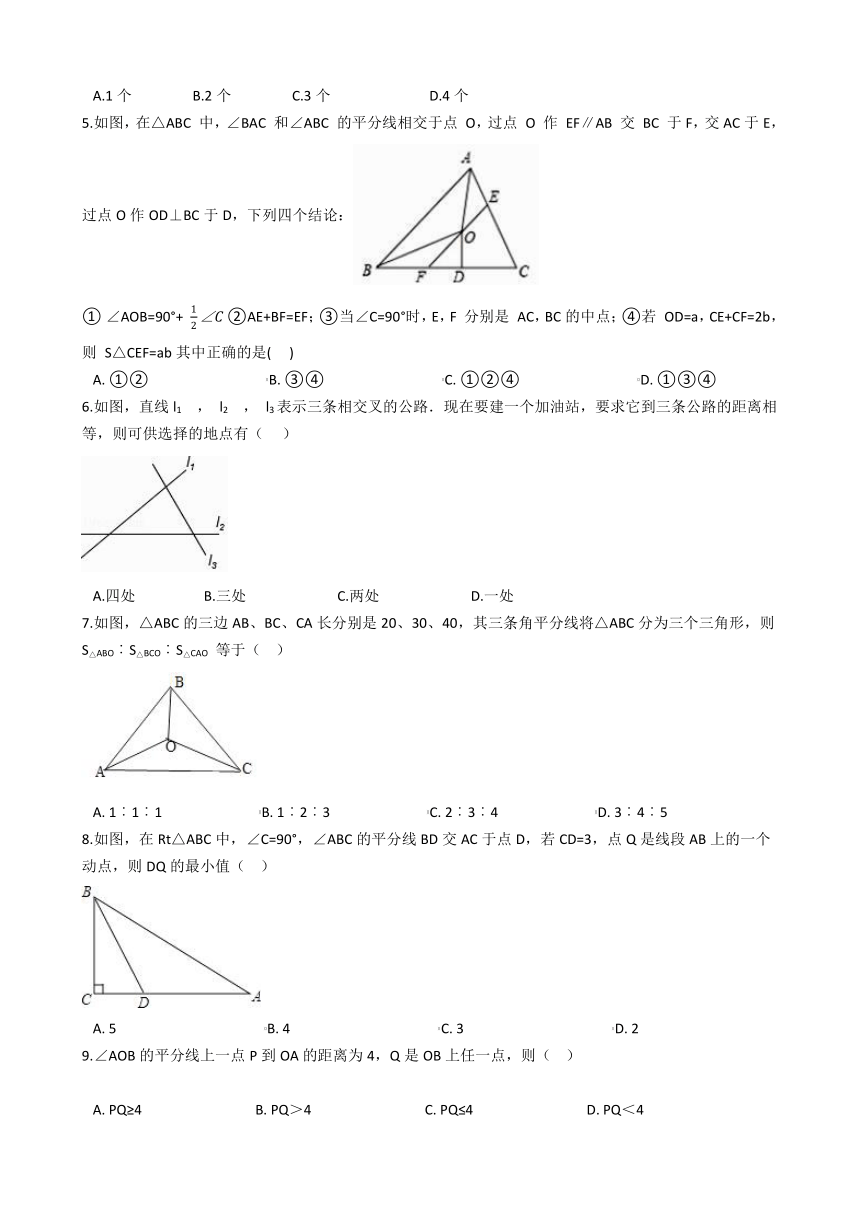
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC 中,∠BAC 和∠ABC 的平分线相交于点 O,过点 O 作 EF∥AB 交 BC 于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:/ ① ∠AOB=90°+
1
2
∠?? ②AE+BF=EF;③当∠C=90°时,E,F 分别是 AC,BC的中点;④若 OD=a,CE+CF=2b,则 S△CEF=ab其中正确的是(??? )
A.?①②??????????????????????????????????/B.?③④??????????????????????????????????/C.?①②④??????????????????????????????????/D.?①③④
6.如图,直线l1 , l2 , l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( ???)
/
A.四处 B.三处 C.两处 D.一处
7.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO 等于( ??) /
A.?1︰1︰1????????????????????????????/B.?1︰2︰3????????????????????????????/C.?2︰3︰4????????????????????????????/D.?3︰4︰5
8.如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若CD=3,点Q是线段AB上的一个动点,则DQ的最小值( ??) /
A.?5???????????????????????????????????????????/B.?4???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?2
9.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( ??)
A.?PQ≥4?????????????????????????????????B.?PQ>4?????????????????????????????????C.?PQ≤4?????????????????????????????????D.?PQ<4
10.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ????) /
A.?角的内部到角的两边的距离相等的点在角的平分线上?????????B.?角平分线上的点到这个角两边的距离相等 C.?三角形三条角平分线的交点到三条边的距离相等?????????D.?以上均不正确
二、填空题(共6题;共8分)
11.如图,要在河流的南边,公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1cm(指图上距离),则图中工厂的位置应在________. /
12.如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE是∠BAC的平分线,点E到AB的距离等于3cm,则CF=________cm.
/
13.如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,BC=9,则S△ABD =________.
/
14.如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=________.
/
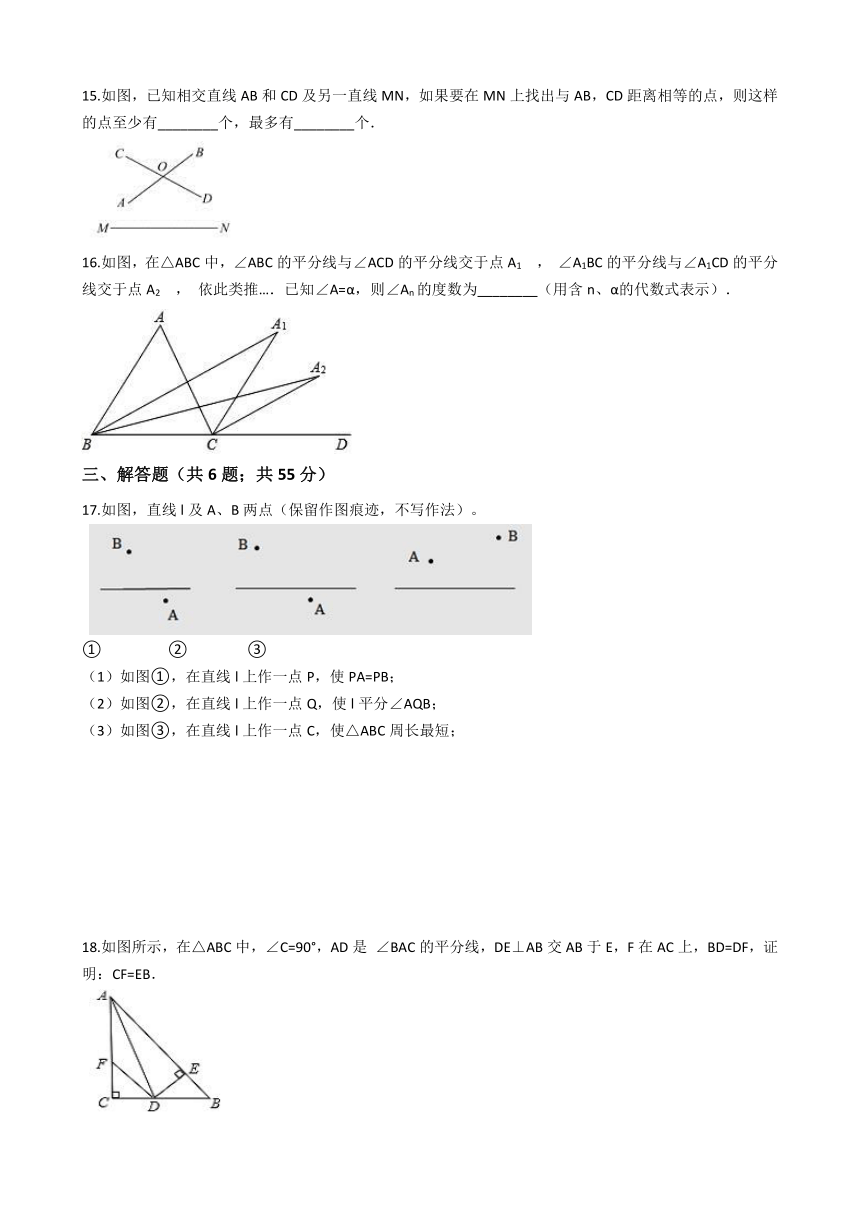
15.如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,则这样的点至少有________个,最多有________个. /
16.如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于点A1 , ∠A1BC的平分线与∠A1CD的平分线交于点A2 , 依此类推….已知∠A=α,则∠An的度数为________(用含n、α的代数式表示).
/
三、解答题(共6题;共55分)
17.如图,直线l及A、B两点(保留作图痕迹,不写作法)。
/
①????????????????? ②????? ??????????③
(1)如图①,在直线l上作一点P,使PA=PB;
(2)如图②,在直线l上作一点Q,使l平分∠AQB;
(3)如图③,在直线l上作一点C,使△ABC周长最短;
18.如图所示,在△ABC中,∠C=90°,AD是 ∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF,证明:CF=EB.
/
19.如图,已知△ABC中,∠ABC和∠ACB的平分线BD、CE相交于点O,且∠A=60°,求∠BOC的度数.
/
20.如图//
(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数.
21.如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
/
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
22.已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
/
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
答案解析部分
一、单选题
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
二、填空题
11.【答案】∠BAC的平分线上,与A相距1cm的地方
12.【答案】3
13.【答案】30
14.【答案】140°;40°
15.【答案】1;2
16.【答案】
1
2
??
??
三、解答题
17.【答案】(1)解:如图
/?
(2)解:如图
/
(3)解:如图
/
18.【答案】证明:∵AD是∠BAC的平分线,DE⊥AB于E,DC⊥AC于C,
∴DE=DC.
又∵BD=DF,
∴Rt△CDF≌Rt△EDB,
∴CF=EB.
19.【答案】解:如图所示,
/
∵∠ABC和∠ACB的平分线BD、CE相交于点O,
∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
1
2
(180°-∠A)=
1
2
(180°-60°)=60°,
故∠BOC=180°-(∠2+∠4)=180°-60°=120°.
20.【答案】(1)解: ∵????=4????,????+????=????∴????=5???? ∵点D是线段????的中点 ∴????=????=
1
2
????=
1
2
???? ∵????=?????????=6???? ∴
5
2
?????????=6???? ∴????=4???? ∴????=4????=16???? (2)解: ∵∠??????=
90
°
,????平分∠??????∴∠??????=
1
2
∠??????=
45
°
∵∠??????=∠???????∠??????=
90
°
?
45
°
, ∠??????=3∠?????? ∴∠??????=
15
°
∴∠??????=∠???????∠??????=
90
°
?
15
°
=
75
°
21.【答案】(1)解:如图,
/
在RT△APR和RT△APS中,
{
????=????
????=????
,
∴RT△APR≌RT△APS(HL),
∴∠BAP=∠1,
∵AQ=PQ,
∴∠1=∠2,
∴∠BAP=∠2,
∴QP∥AR.
(2)解:AR=AS,理由如下:
∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
{
????=????
????=????
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR.
22.【答案】(1)证明:∵BD,CE是△ABC的高,
∴ ∠??????=∠??????=90° ,
∵OB=OC,
∴ ∠??????=∠?????? .
又∵BC是公共边,
∴△BEC≌△CDB(AAS).
∴ ∠??????=∠?????? .
∴△ABC是等腰三角形
(2)解:点O在∠BAC的平分线上.理由如下:
∵△BEC≌△CDB,
∴BD=CE.
∵OB=OC,
∴OD=OE.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上
一、单选题(共10题;共20分)
1.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B。下列结论中不一定成立的是(? )
/
A.PA=PB B.PO平分∠AOB C.OA=OB D.AB垂直平分OP
2.如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3cm,则AB与CD之间的距离为(?? ????)
/
A.3 cm B.6 cm C.9 cm D.无法确定
3.如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C,D为圆心,大于
1
2
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是(??? )
/
A.?△OCD是等腰三角形???????????????????????????????????????????/B.?点E到OA,OB的距离相等 C.?CD垂直平分OE???????????????????????????????????????????????????D.?证明射线OE是角平分线的依据是SSS
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90+
1
2
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则
??
△??????
=mn.其中正确的结论有(??? )
/
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC 中,∠BAC 和∠ABC 的平分线相交于点 O,过点 O 作 EF∥AB 交 BC 于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:/ ① ∠AOB=90°+
1
2
∠?? ②AE+BF=EF;③当∠C=90°时,E,F 分别是 AC,BC的中点;④若 OD=a,CE+CF=2b,则 S△CEF=ab其中正确的是(??? )
A.?①②??????????????????????????????????/B.?③④??????????????????????????????????/C.?①②④??????????????????????????????????/D.?①③④
6.如图,直线l1 , l2 , l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( ???)
/
A.四处 B.三处 C.两处 D.一处
7.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO 等于( ??) /
A.?1︰1︰1????????????????????????????/B.?1︰2︰3????????????????????????????/C.?2︰3︰4????????????????????????????/D.?3︰4︰5
8.如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若CD=3,点Q是线段AB上的一个动点,则DQ的最小值( ??) /
A.?5???????????????????????????????????????????/B.?4???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?2
9.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( ??)
A.?PQ≥4?????????????????????????????????B.?PQ>4?????????????????????????????????C.?PQ≤4?????????????????????????????????D.?PQ<4
10.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ????) /
A.?角的内部到角的两边的距离相等的点在角的平分线上?????????B.?角平分线上的点到这个角两边的距离相等 C.?三角形三条角平分线的交点到三条边的距离相等?????????D.?以上均不正确
二、填空题(共6题;共8分)
11.如图,要在河流的南边,公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1cm(指图上距离),则图中工厂的位置应在________. /
12.如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE是∠BAC的平分线,点E到AB的距离等于3cm,则CF=________cm.
/
13.如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,BC=9,则S△ABD =________.
/
14.如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=________.
/
15.如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,则这样的点至少有________个,最多有________个. /
16.如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于点A1 , ∠A1BC的平分线与∠A1CD的平分线交于点A2 , 依此类推….已知∠A=α,则∠An的度数为________(用含n、α的代数式表示).
/
三、解答题(共6题;共55分)
17.如图,直线l及A、B两点(保留作图痕迹,不写作法)。
/
①????????????????? ②????? ??????????③
(1)如图①,在直线l上作一点P,使PA=PB;
(2)如图②,在直线l上作一点Q,使l平分∠AQB;
(3)如图③,在直线l上作一点C,使△ABC周长最短;
18.如图所示,在△ABC中,∠C=90°,AD是 ∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF,证明:CF=EB.
/
19.如图,已知△ABC中,∠ABC和∠ACB的平分线BD、CE相交于点O,且∠A=60°,求∠BOC的度数.
/
20.如图//
(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数.
21.如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
/
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
22.已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
/
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
答案解析部分
一、单选题
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
二、填空题
11.【答案】∠BAC的平分线上,与A相距1cm的地方
12.【答案】3
13.【答案】30
14.【答案】140°;40°
15.【答案】1;2
16.【答案】
1
2
??
??
三、解答题
17.【答案】(1)解:如图
/?
(2)解:如图
/
(3)解:如图
/
18.【答案】证明:∵AD是∠BAC的平分线,DE⊥AB于E,DC⊥AC于C,
∴DE=DC.
又∵BD=DF,
∴Rt△CDF≌Rt△EDB,
∴CF=EB.
19.【答案】解:如图所示,
/
∵∠ABC和∠ACB的平分线BD、CE相交于点O,
∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
1
2
(180°-∠A)=
1
2
(180°-60°)=60°,
故∠BOC=180°-(∠2+∠4)=180°-60°=120°.
20.【答案】(1)解: ∵????=4????,????+????=????∴????=5???? ∵点D是线段????的中点 ∴????=????=
1
2
????=
1
2
???? ∵????=?????????=6???? ∴
5
2
?????????=6???? ∴????=4???? ∴????=4????=16???? (2)解: ∵∠??????=
90
°
,????平分∠??????∴∠??????=
1
2
∠??????=
45
°
∵∠??????=∠???????∠??????=
90
°
?
45
°
, ∠??????=3∠?????? ∴∠??????=
15
°
∴∠??????=∠???????∠??????=
90
°
?
15
°
=
75
°
21.【答案】(1)解:如图,
/
在RT△APR和RT△APS中,
{
????=????
????=????
,
∴RT△APR≌RT△APS(HL),
∴∠BAP=∠1,
∵AQ=PQ,
∴∠1=∠2,
∴∠BAP=∠2,
∴QP∥AR.
(2)解:AR=AS,理由如下:
∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
{
????=????
????=????
,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR.
22.【答案】(1)证明:∵BD,CE是△ABC的高,
∴ ∠??????=∠??????=90° ,
∵OB=OC,
∴ ∠??????=∠?????? .
又∵BC是公共边,
∴△BEC≌△CDB(AAS).
∴ ∠??????=∠?????? .
∴△ABC是等腰三角形
(2)解:点O在∠BAC的平分线上.理由如下:
∵△BEC≌△CDB,
∴BD=CE.
∵OB=OC,
∴OD=OE.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
