高中数学苏教版选修2-1课件: 1.2 简单的逻辑连接词 课件(23张)
文档属性
| 名称 | 高中数学苏教版选修2-1课件: 1.2 简单的逻辑连接词 课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 20:57:50 | ||
图片预览








文档简介
课件23张PPT。简单的逻辑连接词复习回顾1.命题的定义是什么? 用语言、符号或式子表达的,可以
判断真假的陈述句叫做命题. 2.充分条件、必要条件和充要条件的含义分别是什么?若 ,则称p是q的充分条件,
且q是p的必要条件.
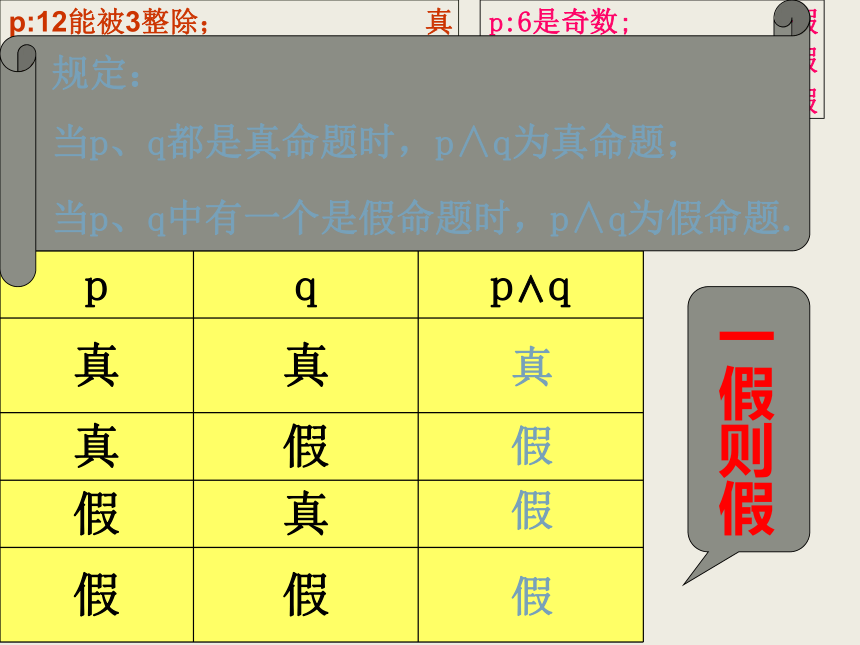
若 ,则p是q的充要条件. 在数学中常常要使用逻辑联结词“或”、“且”、“非”,它们与日常生活中这些词语所表达的含义和用法是不尽相同的,下面我们就分别介绍数学中使用联结词“或”、“且”、“非”联结命题时的含义与用法。 为了叙述简便,今后常用小写字母p,q,r,s,…表示命题。探究(一):逻辑联结词“且”矩形的对角线相等且互相平分. 一、由“且”构成的复合命题定义:一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作 p∧q,读作“p且q”p:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两腰相等且三条中线相等. p:6是奇数;
q:6是素数;
p∧q:6是奇数且是素数. 真真真假假假真假假真假假假例1:将下列命题用“且”联结成新命题,并判断它们的真假:(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分(3)p:35是15的倍数,
q: 35是7的倍数例2、用“且”改写下列命题并判断其真假。2、2和3都是素数。1、1既是奇数,又是素数。解:1 是奇数且 1 是素数 。 假命题解: 2 是素数且 3 是素数。 真命题练习:将下列命题用“且”联结成新命题,并判断真假。
(1)p: 是无理数,q: 大于1;
(2)p:N Z,q:{0} N;
(3)探究(二):逻辑联结词“或”二、由“或”构成的复合命题 定义:一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p ∨ q,读作“p或q”p:12能被3整除;
q:12能被4整除;
p∨q:12能被3整除或能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∨q:等腰三角形两腰相等或三条中线相等. p:6是奇数;
q:6是素数;
p∨q:6是奇数或是素数. 真真假假假假真真真真真真假例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的
两个三角形全等. 解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.小组合作:
1、如果 为真命题,那么 一定
是真命题吗?
2、如果 为真命题,那么 一定
是真命题吗?若p∧q为真,则p∨q为真,反之不成立.探究(三):逻辑联结词“非” 真真真真假假假假一般地,对一个命题p全盘否定,就得到一个新命题,记作﹁p,读作“非p”或“p的否定”。 p与﹁p必有一个是真命题,
另一个是假命题.﹁p的否定是p真假相反
例4:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.﹁p:大于1的数不是正数.否命题:不大于1的数不是正数.注:命题的否定只否定结论否命题则既否定条件也否定结论原命题:“若p,则q”
“若 ,则 ”“若p,则 ”
练习:写出命题p: “正方形的四条边相 等”的否定与它的否命题.
命题p的否定(┓p):
p的否命题:正方形的四条边不相等.若一个四边形不是正方形,则它的四条边不相等. 1.设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.解:若方程x2+mx+1=0有两个不等的负根 即 p: m>2若方程4x2+4(m-2)x+1=0无实根则?=16(m-2)2-16<0,即12、正确应用逻辑联结词“且、或、非”解决问题
3、掌握真值表
课堂小结4、命题的否定与否命题的区别
判断真假的陈述句叫做命题. 2.充分条件、必要条件和充要条件的含义分别是什么?若 ,则称p是q的充分条件,
且q是p的必要条件.
若 ,则p是q的充要条件. 在数学中常常要使用逻辑联结词“或”、“且”、“非”,它们与日常生活中这些词语所表达的含义和用法是不尽相同的,下面我们就分别介绍数学中使用联结词“或”、“且”、“非”联结命题时的含义与用法。 为了叙述简便,今后常用小写字母p,q,r,s,…表示命题。探究(一):逻辑联结词“且”矩形的对角线相等且互相平分. 一、由“且”构成的复合命题定义:一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作 p∧q,读作“p且q”p:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两腰相等且三条中线相等. p:6是奇数;
q:6是素数;
p∧q:6是奇数且是素数. 真真真假假假真假假真假假假例1:将下列命题用“且”联结成新命题,并判断它们的真假:(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分(3)p:35是15的倍数,
q: 35是7的倍数例2、用“且”改写下列命题并判断其真假。2、2和3都是素数。1、1既是奇数,又是素数。解:1 是奇数且 1 是素数 。 假命题解: 2 是素数且 3 是素数。 真命题练习:将下列命题用“且”联结成新命题,并判断真假。
(1)p: 是无理数,q: 大于1;
(2)p:N Z,q:{0} N;
(3)探究(二):逻辑联结词“或”二、由“或”构成的复合命题 定义:一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p ∨ q,读作“p或q”p:12能被3整除;
q:12能被4整除;
p∨q:12能被3整除或能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∨q:等腰三角形两腰相等或三条中线相等. p:6是奇数;
q:6是素数;
p∨q:6是奇数或是素数. 真真假假假假真真真真真真假例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的
两个三角形全等. 解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.小组合作:
1、如果 为真命题,那么 一定
是真命题吗?
2、如果 为真命题,那么 一定
是真命题吗?若p∧q为真,则p∨q为真,反之不成立.探究(三):逻辑联结词“非” 真真真真假假假假一般地,对一个命题p全盘否定,就得到一个新命题,记作﹁p,读作“非p”或“p的否定”。 p与﹁p必有一个是真命题,
另一个是假命题.﹁p的否定是p真假相反
例4:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.﹁p:大于1的数不是正数.否命题:不大于1的数不是正数.注:命题的否定只否定结论否命题则既否定条件也否定结论原命题:“若p,则q”
“若 ,则 ”“若p,则 ”
练习:写出命题p: “正方形的四条边相 等”的否定与它的否命题.
命题p的否定(┓p):
p的否命题:正方形的四条边不相等.若一个四边形不是正方形,则它的四条边不相等. 1.设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.解:若方程x2+mx+1=0有两个不等的负根 即 p: m>2若方程4x2+4(m-2)x+1=0无实根则?=16(m-2)2-16<0,即1
3、掌握真值表
课堂小结4、命题的否定与否命题的区别
