高中数学苏教版选修2-1课件: 2.5 圆锥曲线的统一定义 课件(22张)
文档属性
| 名称 | 高中数学苏教版选修2-1课件: 2.5 圆锥曲线的统一定义 课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 21:01:13 | ||
图片预览






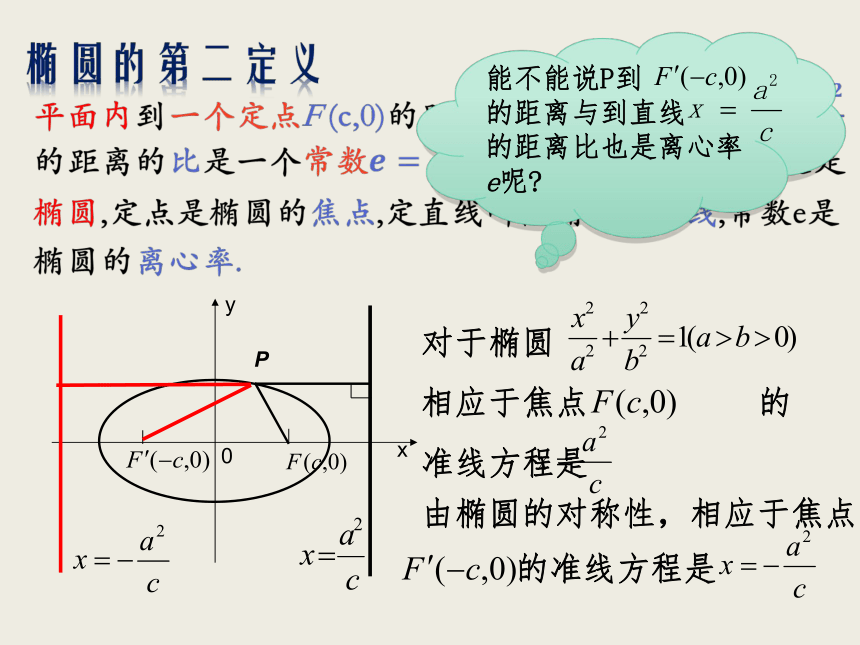


文档简介
课件22张PPT。用一个平面去截取一个圆锥面,当平面经过圆锥面的顶点时,可得到两条相交直线;当平面与圆锥面的轴垂直时,截得的图形是一个圆。改变上述平面的位置,截得圆锥面还能得到椭圆抛物线双曲线 1.平面内到两定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距. 2.平面内与两定点F1、F2的距离的差的绝对值是常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两个焦点之间的距离叫做焦距.3.平面内到一个定点F和一条定直线l (F不在l上)距离相等的点的轨迹叫做抛物线,同为圆锥曲线,得到方式有很类似,为何他们定义区别较大 ?3.平面内到一个定点F 的距离与它到一条定直线l (F不在l上)的距离的比是1的点的轨迹叫做抛物线.定点叫做抛物线的焦点,定直线l叫做抛物线的准线问题一已知动点P(x,y)到定点F(3,0)的距离与它到定直线l: 的距离之比等于 ,求动点P的轨迹.
点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于F(3,0)已知若F(c,0)则动点P的轨迹是椭圆.猜想将上式两边平方并化简得:P证明:由已知,得证明猜想 点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于若F(c,0) (0(0 当0< e <1 时, 点的轨迹是椭圆. 当 e >1 时, 点的轨迹是双曲线. 当 e =1 时, 点的轨迹是抛物线.定点F是圆锥曲线的焦点,定直线l叫做圆锥曲线的准线,常数e是圆锥曲线的离心率.
OxyPF1F2OyxPF1F2右准线上准线下准线左准线 例1 求中心在原点,一条准线方程是x=3,
离心率为 的椭圆标准方程.解:依题意设椭圆标准方程为例2 椭圆方程为 ,其上有一点P,它
到右焦点的距离为14,求P点到左准线的距离.P解:由椭圆的方程可知由第一定义可知:由第二定义知:例3 :若椭圆 内有一点P(1,-1),F为右焦
点,在该椭圆上求一点M,使得 最小,并且求最小值.OxyMFPCA.线段 B.圆 C.椭圆 D.无法确定1.椭圆 上一点P到一个焦点的距离为3,则它到相对应的准线的距离为 . 2.点P与点F(2,0)的距离是它到直线x=8的距离的一半,
则点P的轨迹方程为 .5.已知椭圆 上的三点的横坐标成等差数列,求证这三点到同一焦点的距离也成等差数列.课堂练习4. 设AB是过椭圆焦点F的弦,以AB为直径的圆与F所
对应的准线的位置关系是( )A.相离 B.相切 C.相交 D.无法确定A|PF2|=a-ex0,|PF1|=a+ex0P(x0,y0)是椭圆 上一点,
e是椭圆的离心率.证明:焦半径公式: |PF2|=a-ex0,|PF1|=a+ex0证明:例1:求下列椭圆的焦点坐标和准线(1)(2) 2x2+y2=8 焦点坐标:(0,-2),(0,2). 准线方程:y= ±4(1)猜想中有哪些已知条件?
(2)定点、比在椭圆中分别指什么?
(3)比的取值范围是什么? 点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于若F(c,0)则动点P的轨迹是椭圆.
点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于F(3,0)已知若F(c,0)则动点P的轨迹是椭圆.猜想将上式两边平方并化简得:P证明:由已知,得证明猜想 点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于若F(c,0) (0
OxyPF1F2OyxPF1F2右准线上准线下准线左准线 例1 求中心在原点,一条准线方程是x=3,
离心率为 的椭圆标准方程.解:依题意设椭圆标准方程为例2 椭圆方程为 ,其上有一点P,它
到右焦点的距离为14,求P点到左准线的距离.P解:由椭圆的方程可知由第一定义可知:由第二定义知:例3 :若椭圆 内有一点P(1,-1),F为右焦
点,在该椭圆上求一点M,使得 最小,并且求最小值.OxyMFPCA.线段 B.圆 C.椭圆 D.无法确定1.椭圆 上一点P到一个焦点的距离为3,则它到相对应的准线的距离为 . 2.点P与点F(2,0)的距离是它到直线x=8的距离的一半,
则点P的轨迹方程为 .5.已知椭圆 上的三点的横坐标成等差数列,求证这三点到同一焦点的距离也成等差数列.课堂练习4. 设AB是过椭圆焦点F的弦,以AB为直径的圆与F所
对应的准线的位置关系是( )A.相离 B.相切 C.相交 D.无法确定A|PF2|=a-ex0,|PF1|=a+ex0P(x0,y0)是椭圆 上一点,
e是椭圆的离心率.证明:焦半径公式: |PF2|=a-ex0,|PF1|=a+ex0证明:例1:求下列椭圆的焦点坐标和准线(1)(2) 2x2+y2=8 焦点坐标:(0,-2),(0,2). 准线方程:y= ±4(1)猜想中有哪些已知条件?
(2)定点、比在椭圆中分别指什么?
(3)比的取值范围是什么? 点P(x,y)到定点 的距离与它到定
直线l: 的距离之比等于若F(c,0)则动点P的轨迹是椭圆.
