五年级下册数学课件1.5 综合练习 圆青岛版(五年制)(共16张PPT)
文档属性
| 名称 | 五年级下册数学课件1.5 综合练习 圆青岛版(五年制)(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 906.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 15:29:59 | ||
图片预览





文档简介
课件16张PPT。综合练习复习旧知课堂小结课后作业圆课堂练习1本单元,我们学习了圆的知识。认识了圆各部分的名称,了解了半径、直径直径的关系。同一个圆中,半径是直径的一半。复习旧知返回如果已知圆的半径或直径,我们可以利用
圆的周长计算公式,直接求出圆的周长。如果已知圆的半径可以直接求圆的面积,
如果知道圆的直径,可以先求出半径,然
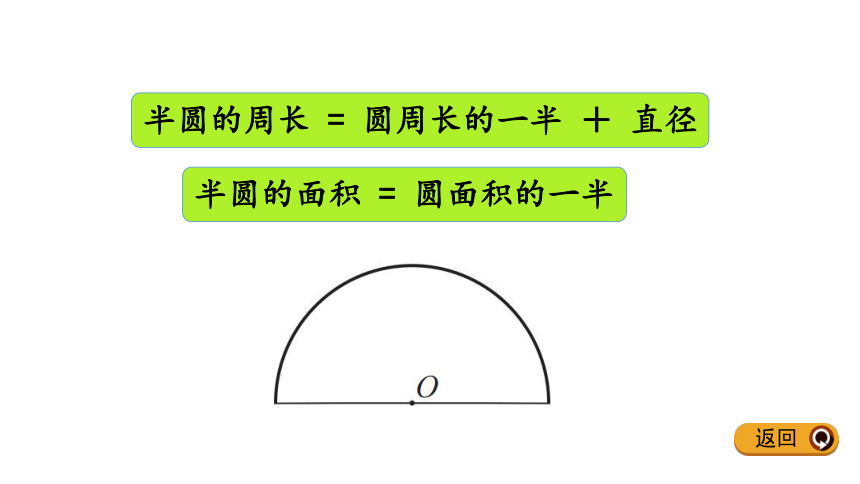
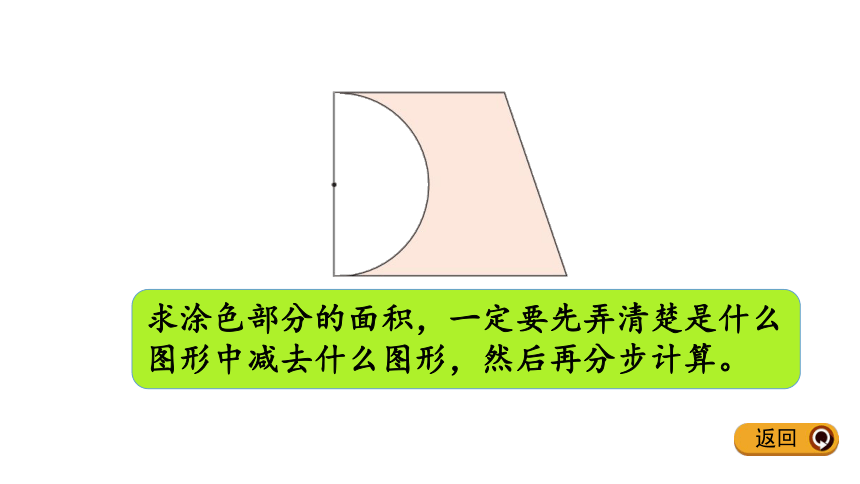
后再求圆的面积。复习旧知返回半圆的周长 = 圆周长的一半 + 直径半圆的面积 = 圆面积的一半返回求涂色部分的面积,一定要先弄清楚是什么
图形中减去什么图形,然后再分步计算。返回求下列图形的周长和面积。20mm40dmC =πd
=3.14×20
=62.8(mm)S=πr2
=3.14×=3.14×100=314(mm2)C = +dS=πr2÷2
=3.14× 2=3.14×200=628(dm2) =3.14× +40
=62.8+40
=102.8(dm)课堂练习返回算一算。3.14×2= 3.14×3= 3.14×4= 3.14×5= 3.14×6= 3.14×7= 3.14×8= 3.14×9= 6.289.4212.5615.718.8421.9825.1228.26这些计算如果我们能背诵下来,对我们计算会有很大的帮助!返回日本富士山是世界最著名的火山之一,底座直径约40千米。富士山的占地面积约是多少平方千米。40÷2=20(千米)S=πr2
=3.14×202
=3.14×400
=1256(平方千米)答:富士山的占地面积约是1256平方千米。返回一粒小石子投到平静的水中,水波大约可传5米;一片落叶掉到水中,水波大约可传1米。哪一种物体产生的水波面积大?大多少?答:小石子产生的水波面积大,大75.36平方米。 水波传送的距离相当是圆的半径。S=πr2
=3.14×52
=3.14×25
=78.5(m2)S=πr2
=3.14×12
=3.14×1
=3.14(m2)78.5-3.14=75.36(m2)返回计算下面各图涂色部分的面积。(单位:cm)S=πr2÷2
=3.14×52÷2
=78.5÷2
=39.25(cm2)S=ab
=10×5
=50(cm2)50-39.25=10.75(cm2)S=πr2÷2
=3.14× 2÷2
=50.24÷2
=25.12(cm2)S= (a+b)×h68-25.12=42.88(cm2) = (10+7)×8 =68(cm2)返回右图是一张光盘及其示意图。图中环形的面积大约是多少平方厘米?(得数保留整数)答:图中环形面积大约是111平方厘米。3.14×(12÷2)2-3.14×(1.6÷2)2环形面积=外圆面积-内圆面积= 111.0304(平方厘米)= 3.14 ×36-3.14 ×0.64= 113.04-2.0096≈111(平方厘米)返回一个圆形花坛,原来直径是15米,扩建后的直径与原来的比是4:3。扩建后花坛的周长和面积各是多少? 4:3= 答:扩建后花坛的周长是62.8m,面积是314m2。15× =20(米)C =πd
=3.14×20
=62.8(m)S=πr2
=3.14×=3.14×100=314(m2)返回答:我发现大圆的周长等于两个小圆的周长之和。如图,小圆的直径长3厘米。
(1)比较大圆的周长与两个小圆周长之和,你发现了什么?
(2)比较大圆的面积与两个小圆面积之和,你发现了什么?从图中可以得出:小圆的直径是大圆的半径C大 =2πr
=2×3.14×3
=18.84(cm)C小 =πd
=3.14×3
=9.42(cm)9.42×2=18.84(cm)返回答:我发现大圆的面积比小圆的面积大,大圆面积是小圆面积的2倍。如图,小圆的直径长3厘米。
(1)比较大圆的周长与两个小圆周长之和,你发现了什么?
(2)比较大圆的面积与两个小圆面积之和,你发现了什么?从图中可以得出:小圆的直径是大圆的半径。7.065×2=14.13(cm)S大=πr2
=3.14×32
=3.14×9
=28.26(cm2)S大=πr2
=3.14×
=3.14×2.25
=7.065(cm2)返回这节课你们都学会了哪些知识?C=2πr或C=πd d=C÷π r=C÷π÷2 S=πr2对不规则的图形,要使用转化的数学思想,把它转化成我们学习过的图形进行计算。返回课堂小结课本:
第18页第10、12题返回课后作业
圆的周长计算公式,直接求出圆的周长。如果已知圆的半径可以直接求圆的面积,
如果知道圆的直径,可以先求出半径,然
后再求圆的面积。复习旧知返回半圆的周长 = 圆周长的一半 + 直径半圆的面积 = 圆面积的一半返回求涂色部分的面积,一定要先弄清楚是什么
图形中减去什么图形,然后再分步计算。返回求下列图形的周长和面积。20mm40dmC =πd
=3.14×20
=62.8(mm)S=πr2
=3.14×=3.14×100=314(mm2)C = +dS=πr2÷2
=3.14× 2=3.14×200=628(dm2) =3.14× +40
=62.8+40
=102.8(dm)课堂练习返回算一算。3.14×2= 3.14×3= 3.14×4= 3.14×5= 3.14×6= 3.14×7= 3.14×8= 3.14×9= 6.289.4212.5615.718.8421.9825.1228.26这些计算如果我们能背诵下来,对我们计算会有很大的帮助!返回日本富士山是世界最著名的火山之一,底座直径约40千米。富士山的占地面积约是多少平方千米。40÷2=20(千米)S=πr2
=3.14×202
=3.14×400
=1256(平方千米)答:富士山的占地面积约是1256平方千米。返回一粒小石子投到平静的水中,水波大约可传5米;一片落叶掉到水中,水波大约可传1米。哪一种物体产生的水波面积大?大多少?答:小石子产生的水波面积大,大75.36平方米。 水波传送的距离相当是圆的半径。S=πr2
=3.14×52
=3.14×25
=78.5(m2)S=πr2
=3.14×12
=3.14×1
=3.14(m2)78.5-3.14=75.36(m2)返回计算下面各图涂色部分的面积。(单位:cm)S=πr2÷2
=3.14×52÷2
=78.5÷2
=39.25(cm2)S=ab
=10×5
=50(cm2)50-39.25=10.75(cm2)S=πr2÷2
=3.14× 2÷2
=50.24÷2
=25.12(cm2)S= (a+b)×h68-25.12=42.88(cm2) = (10+7)×8 =68(cm2)返回右图是一张光盘及其示意图。图中环形的面积大约是多少平方厘米?(得数保留整数)答:图中环形面积大约是111平方厘米。3.14×(12÷2)2-3.14×(1.6÷2)2环形面积=外圆面积-内圆面积= 111.0304(平方厘米)= 3.14 ×36-3.14 ×0.64= 113.04-2.0096≈111(平方厘米)返回一个圆形花坛,原来直径是15米,扩建后的直径与原来的比是4:3。扩建后花坛的周长和面积各是多少? 4:3= 答:扩建后花坛的周长是62.8m,面积是314m2。15× =20(米)C =πd
=3.14×20
=62.8(m)S=πr2
=3.14×=3.14×100=314(m2)返回答:我发现大圆的周长等于两个小圆的周长之和。如图,小圆的直径长3厘米。
(1)比较大圆的周长与两个小圆周长之和,你发现了什么?
(2)比较大圆的面积与两个小圆面积之和,你发现了什么?从图中可以得出:小圆的直径是大圆的半径C大 =2πr
=2×3.14×3
=18.84(cm)C小 =πd
=3.14×3
=9.42(cm)9.42×2=18.84(cm)返回答:我发现大圆的面积比小圆的面积大,大圆面积是小圆面积的2倍。如图,小圆的直径长3厘米。
(1)比较大圆的周长与两个小圆周长之和,你发现了什么?
(2)比较大圆的面积与两个小圆面积之和,你发现了什么?从图中可以得出:小圆的直径是大圆的半径。7.065×2=14.13(cm)S大=πr2
=3.14×32
=3.14×9
=28.26(cm2)S大=πr2
=3.14×
=3.14×2.25
=7.065(cm2)返回这节课你们都学会了哪些知识?C=2πr或C=πd d=C÷π r=C÷π÷2 S=πr2对不规则的图形,要使用转化的数学思想,把它转化成我们学习过的图形进行计算。返回课堂小结课本:
第18页第10、12题返回课后作业
