四年级下册数学课件8.1乒乓球与盒子 北京版 (共23张PPT)
文档属性
| 名称 | 四年级下册数学课件8.1乒乓球与盒子 北京版 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 16:11:39 | ||
图片预览





文档简介
课件23张PPT。游戏——抢椅子游戏规则:
游戏“开始”时,3位同学跟着音乐绕着两把椅子走,当音乐“停”时,3位同学都要坐在椅子上。乒乓球与盒子
小组合作把3支笔放进2个笔筒中,有几种放法?在学习单上完成。每一种摆法中,最多放进了几支笔?小组合作
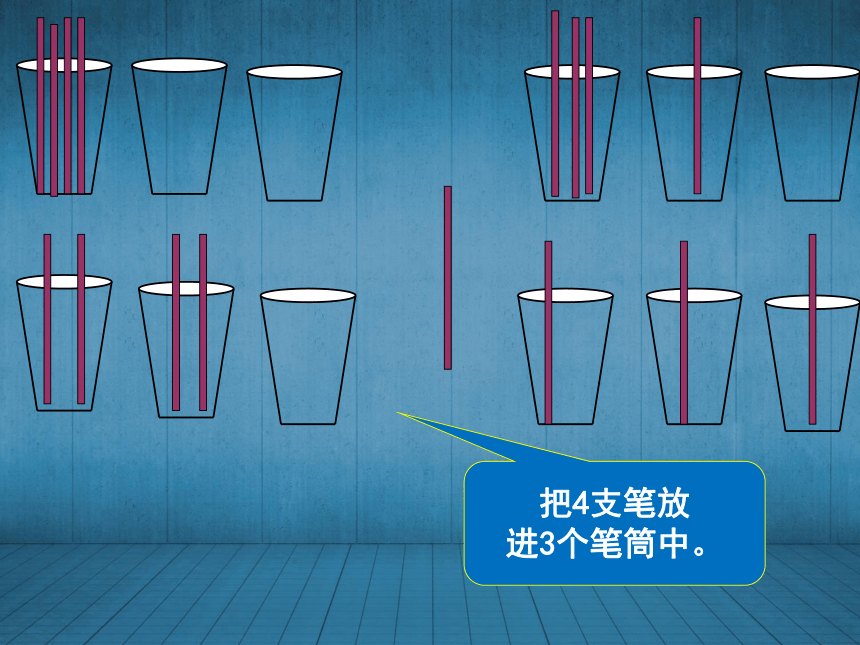
把4支笔放
进3个笔筒中。 看看有几种摆法?
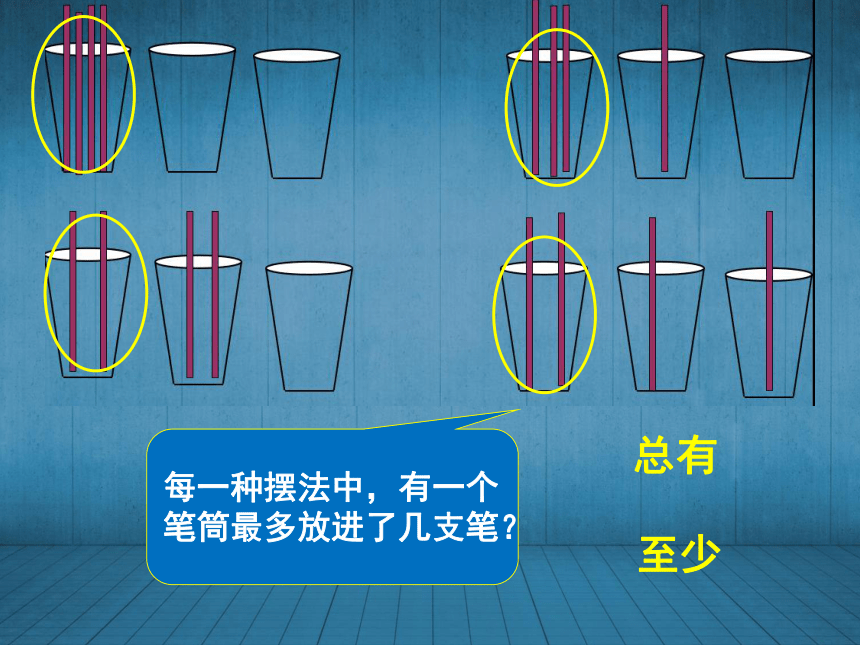
每一种摆法中,最多放进了几支笔?把4支笔放
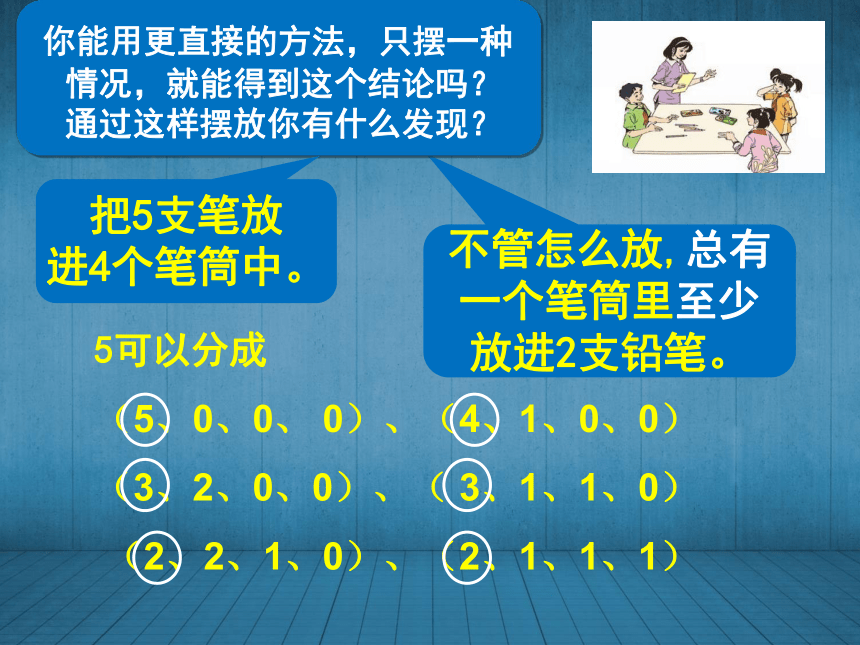
进3个笔筒中。 至少总有每一种摆法中,有一个笔筒最多放进了几支笔?不管怎么放,总有一个笔筒里至少放进2支铅笔。 你能用更直接的方法,只摆一种情况,就能得到这个结论吗?通过这样摆放你有什么发现?把5支笔放
进4个笔筒中。5可以分成
(5、0、0、 0)、(4、1、0、0)
(3、2、0、0)、( 3、1、1、0)
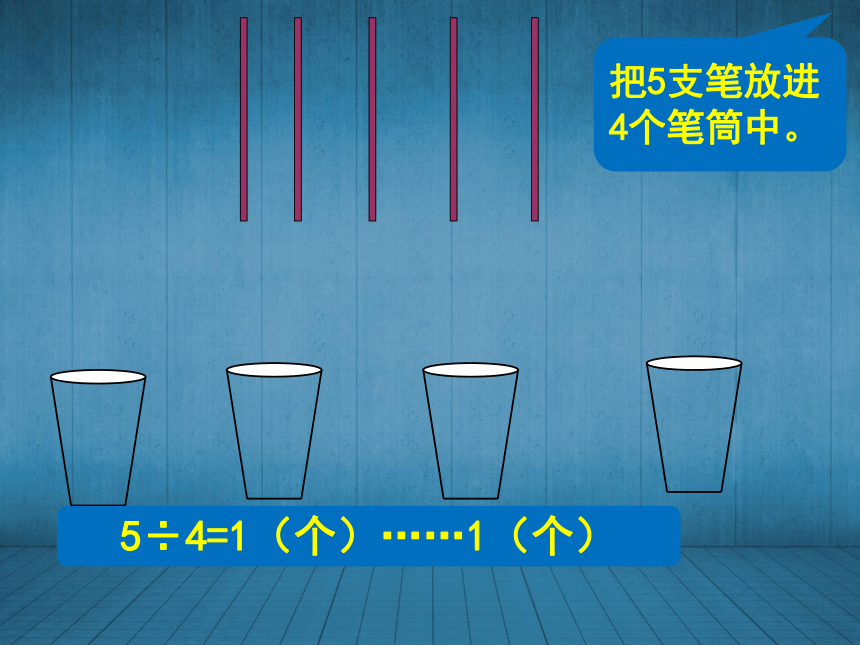
(2、2、1、0)、(2、1、1、1) 把5支笔放进4个笔筒中。5÷4=1(个)……1(个)
如果A、B、C、D四个收款台暂时无人,这时有5个人同时要交钱,那么总会有一个收款台至少会有几个人?
(2个)如果把6个苹果放入5个抽屉中,至少有几个放到同一个抽屉里?如果把7个苹果放入6个抽屉中,至少有几个放到同一个抽屉里呢?如果把100个苹果放入99个抽屉中,至少有几个放到同一个抽屉里呢?(2个)(2个)(2个)1.如果把6个苹果放入4个抽屉中,至少有几个苹果被放到同一个抽屉里呢?请你想一想2.如果把8个苹果放入5个抽屉中,至少有几个苹果被放到同一个抽屉里呢?(2个)(2个) “ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”,也称为“鸽巢原理”。
“抽屉原理” 的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。“抽屉原理”类问题解决模式:
先确定“待分物体”和“抽屉”
再“平均分”
有余数:至少数=商+1(整除时 至少数=商数)
一副扑克牌(除去大小王)52张中有四种花色,从中随意抽5张牌,无论怎么抽, 至少有两张牌是同一花色的,为什么?大家玩过石头、剪刀、布的游戏吗?同桌两人合作,任意划手四次,至少有( )次划出的手势是一样的。想:把什么当作抽屉,把什么当作要分的物体?2
猜一猜:
1.有红色和蓝色两种颜色的棋子,一次摸出2个棋子,有几种情况?观察出现的情况,结果是( )摸出2个同色的棋子。
(选择“可能”或“一定”填空)可能游戏—摸棋子有两种颜色,摸3个球,就能保证有两个球同色.只要摸出的球比它们的颜色种数多1,就能保证有两个球同色.猜一猜:
2.一次摸出3个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。
(选择“可能”或“一定”填空)一定请观察,摸出球的个数与颜色种数有什么关系?摸出球的个数比颜色种数多1。 一盒围棋棋子,黑白子混放,我们任意摸出( )个棋子,至少有2个棋子是同颜色的,为什么? 3游戏—摸棋子在我们学校的任意13人中,总有至少几个人的属相相同,想一想,为什么?我们班有40名同学,那么至少有( )名同学的生日在同一个月?为什么? 4
游戏“开始”时,3位同学跟着音乐绕着两把椅子走,当音乐“停”时,3位同学都要坐在椅子上。乒乓球与盒子
小组合作把3支笔放进2个笔筒中,有几种放法?在学习单上完成。每一种摆法中,最多放进了几支笔?小组合作
把4支笔放
进3个笔筒中。 看看有几种摆法?
每一种摆法中,最多放进了几支笔?把4支笔放
进3个笔筒中。 至少总有每一种摆法中,有一个笔筒最多放进了几支笔?不管怎么放,总有一个笔筒里至少放进2支铅笔。 你能用更直接的方法,只摆一种情况,就能得到这个结论吗?通过这样摆放你有什么发现?把5支笔放
进4个笔筒中。5可以分成
(5、0、0、 0)、(4、1、0、0)
(3、2、0、0)、( 3、1、1、0)
(2、2、1、0)、(2、1、1、1) 把5支笔放进4个笔筒中。5÷4=1(个)……1(个)
如果A、B、C、D四个收款台暂时无人,这时有5个人同时要交钱,那么总会有一个收款台至少会有几个人?
(2个)如果把6个苹果放入5个抽屉中,至少有几个放到同一个抽屉里?如果把7个苹果放入6个抽屉中,至少有几个放到同一个抽屉里呢?如果把100个苹果放入99个抽屉中,至少有几个放到同一个抽屉里呢?(2个)(2个)(2个)1.如果把6个苹果放入4个抽屉中,至少有几个苹果被放到同一个抽屉里呢?请你想一想2.如果把8个苹果放入5个抽屉中,至少有几个苹果被放到同一个抽屉里呢?(2个)(2个) “ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”,也称为“鸽巢原理”。
“抽屉原理” 的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。“抽屉原理”类问题解决模式:
先确定“待分物体”和“抽屉”
再“平均分”
有余数:至少数=商+1(整除时 至少数=商数)
一副扑克牌(除去大小王)52张中有四种花色,从中随意抽5张牌,无论怎么抽, 至少有两张牌是同一花色的,为什么?大家玩过石头、剪刀、布的游戏吗?同桌两人合作,任意划手四次,至少有( )次划出的手势是一样的。想:把什么当作抽屉,把什么当作要分的物体?2
猜一猜:
1.有红色和蓝色两种颜色的棋子,一次摸出2个棋子,有几种情况?观察出现的情况,结果是( )摸出2个同色的棋子。
(选择“可能”或“一定”填空)可能游戏—摸棋子有两种颜色,摸3个球,就能保证有两个球同色.只要摸出的球比它们的颜色种数多1,就能保证有两个球同色.猜一猜:
2.一次摸出3个球,有几种情况?观察出现的情况,结果是( )摸出2个同色的球。
(选择“可能”或“一定”填空)一定请观察,摸出球的个数与颜色种数有什么关系?摸出球的个数比颜色种数多1。 一盒围棋棋子,黑白子混放,我们任意摸出( )个棋子,至少有2个棋子是同颜色的,为什么? 3游戏—摸棋子在我们学校的任意13人中,总有至少几个人的属相相同,想一想,为什么?我们班有40名同学,那么至少有( )名同学的生日在同一个月?为什么? 4
