北师大版八年级数学下册1.2直角三角形同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学下册1.2直角三角形同步练习(含答案) | 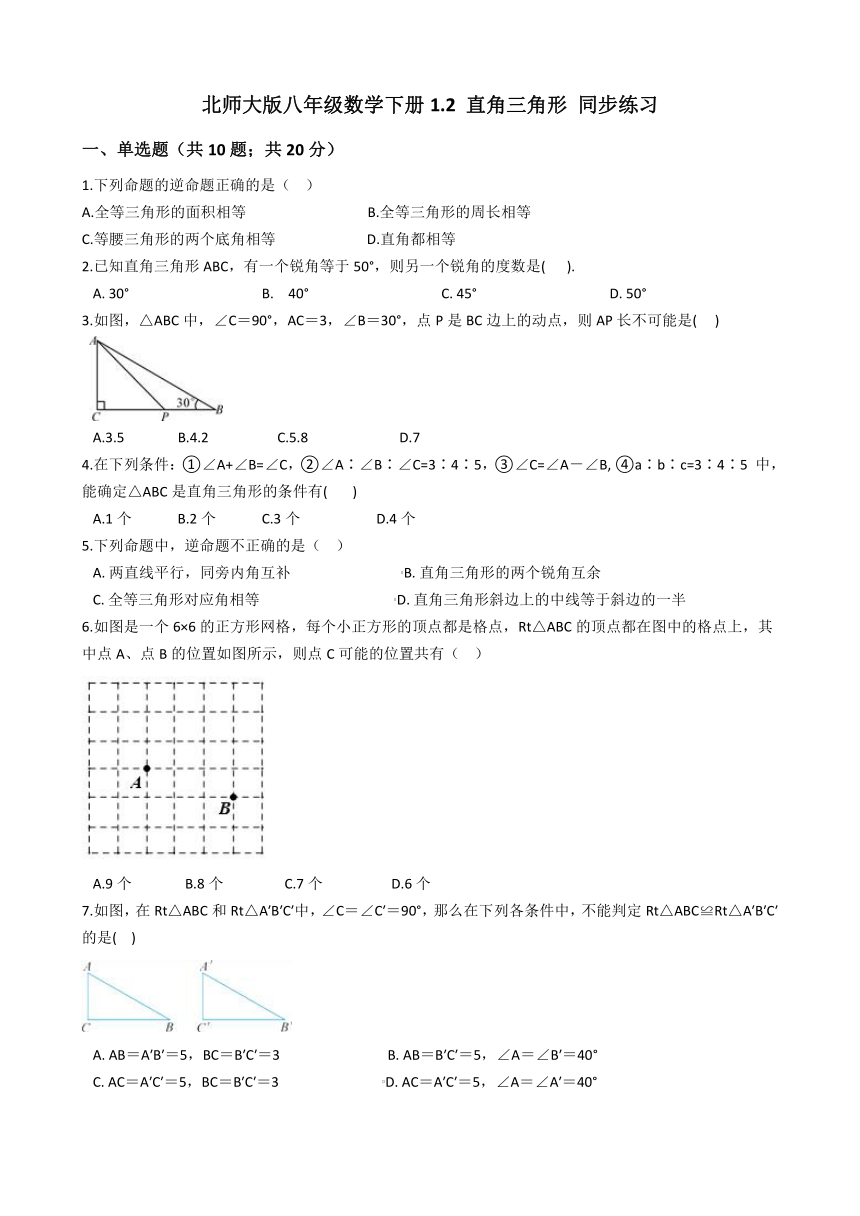 | |
| 格式 | zip | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-01 23:48:33 | ||
图片预览




文档简介
北师大版八年级数学下册1.2 直角三角形 同步练习
一、单选题(共10题;共20分)
1.下列命题的逆命题正确的是(?? )
A.全等三角形的面积相等 B.全等三角形的周长相等 C.等腰三角形的两个底角相等 D.直角都相等
2.已知直角三角形ABC,有一个锐角等于50°,则另一个锐角的度数是(???? ).
A.?30°??????????????????????????????????????/B.?? 40°??????????????????????????????????????/C.?45°??????????????????????????????????????/D.?50°
3.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是(??? )
/
A.3.5 B.4.2 C.5.8 D.7
4.在下列条件:①∠A+∠B=∠C,②∠A∶∠B∶∠C=3∶4∶5,③∠C=∠A-∠B, ④a∶b∶c=3∶4∶5 中,能确定△ABC是直角三角形的条件有(????? )
A.1个 B.2个 C.3个 D.4个
5.下列命题中,逆命题不正确的是(?? )
A.?两直线平行,同旁内角互补????????????????????????????????/B.?直角三角形的两个锐角互余 C.?全等三角形对应角相等???????????????????????????????????????/D.?直角三角形斜边上的中线等于斜边的一半
6.如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都在图中的格点上,其中点A、点B的位置如图所示,则点C可能的位置共有( ??)
/
A.9个 B.8个 C.7个 D.6个
7.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是(?? ) /
A.?AB=A′B′=5,BC=B′C′=3???????????????????????????????/B.?AB=B′C′=5,∠A=∠B′=40° C.?AC=A′C′=5,BC=B′C′=3??????????????????????????????/D.?AC=A′C′=5,∠A=∠A′=40°
8.如图,AD是Rt△ABC斜边BC上的高,将△ACD沿AD所在的直线折叠,点C恰好落在BC的中点E处,则∠B等于(?? )
/
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?45°???????????????????????????????????????D.?60°
9.若△ABC三边长a,b,c满足
??+???32
+ |b-a-2| + (c-8)2=0,则△ABC是(??? )
A.?等腰三角形????????????????????/B.?等边三角形????????????????????/C.?直角三角形????????????????????/D.?等腰直角三角形
10.如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为(??????? ).
/
A.?
7
4
????????????????????????????????/B.?1????????????????????????????????/C.?
7
4
或1或
9
4
????????????????????????????????/D.?
7
4
或1或
11
4
二、填空题(共7题;共7分)
11.命题“在同一个三角形中,等角对等边”的逆命题是________.
12.若一个三角形三边长分别为 1.5,2,2.5,则这个三角形一定是________三角形.
13.如图,山坡的倾斜角∠ABC为30°,小明沿山坡BA从山脚B点步行到山顶A共走了100m,则山顶的高度AC是________m.
/
14.用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是________.
15.如图,在△ABC中,∠ABC=90°,∠A=50°,CD=CB,∠ABD=________.
/
16.将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是________cm2/
17.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为
65
,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为
65
时,正方形EFGH的面积的所有可能值是________(不包括5).
/
三、解答题(共6题;共52分)
18.如图,△ABC中,AB=AC,D点在BC上,∠1=30°,且∠4=60°,
/
求证:
(1)AD=BD;
(2)CD=2BD.
19.如图,在△ABC中,∠BAC=∠ABC,点P在AB上,如果AD⊥CP,BE⊥CP的延长线,垂足分别为D,E,且BE=CD.
/
(1)试探求这个图形中还有哪些相等的线段,并给出证明;
(2)试确定△ABC的形状.
20.如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
/
21.如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE. /
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
22.如图所示,在△ACB中,∠ACB=90°,∠1=∠B. /
(1)求证:CD⊥AB;
(2)如果AC=8,BC=6,AB=10,求CD的长.
23.边长为6的等边△ABC中,点P从点A出发沿射线AB方向移动,同时点Q从点B出发,以相同的速度沿射线BC方向移动,连接AQ、CP,直线AQ、CP相交于点D.
/??? /
(1)如图①,当点P、Q分别在边AB、BC上时,
①连接PQ,当△BPQ是直角三角形时,AP等于________;
②∠CDQ的大小是否随P,Q的运动而变化?如果不会,请求出∠CDQ的度数;如果会,请说明理由;________
(2)当P、Q分别在边AB、BC的延长线上时,在图②中画出点D,并直接写出∠CDQ的度数.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】在同一个三角形中,等边对等角
12.【答案】直角
13.【答案】50
14.【答案】/a<b<a
15.【答案】20°
16.【答案】2
17.【答案】9或13或49
三、解答题
18.【答案】(1)证明:∵∠4=60°,∠1=30°,
∴∠ABD=∠4-∠1=60°-30°=30°=∠1.
∴BD=AD
(2)证明:∵∠ABD=30°,
又∵AB=AC,
∴∠C=∠ABD=30°,
∴∠2=180°-∠4-∠C=180°-60°-30°=90°,
∵∠C=30°,
∴CD=2AD=2BD
19.【答案】(1)解:图中相等的线段还有AC=BC,CE=AD.
证明:∵∠BAC=∠ABC, ∴AC=BC.
∵AD⊥CP,BE⊥CP,
∴∠ADC=∠BEC=90°.
又∵BE=CD,
∴Rt△BCE≌Rt△CAD(HL).???????
∴CE=AD 。
(2)解:△ABC为等腰直角三角形,理由如下 : ∵△BCE≌△CAD,
∴∠EBC=∠ACD.
∵∠EBC+∠BCE=90°,
∴∠ACD+∠BCE=90°,即∠ACB=90°. 又AC=BC ,
∴△ABC为等腰直角三角形 。
20.【答案】解:连接BD
/
在Rt△ABD中,BD2=AB2+AD2=32+42=52 ,
在△CBD中,CD2=132 , BC2=122 , 而122+52=132 , 即BC2+BD2=CD2 ,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=
1
2
AD·AB+
1
2
DB· BC=
1
2
×4×3+
1
2
×5×12=36
所以需费用36×200=7200(元)
21.【答案】(1)解:画出高AD,AF,如图所示./ (2)解:猜想:BC=BE.证明如下: ∵AD⊥BC,AF⊥BE, ∴△ACD,△AEF,△ABD,△ABF都是直角三角形. 在Rt△ACD和Rt△AEF中, {
????=????
????=????
∴Rt△ACD≌Rt△AEF(HL). ∴CD=EF(全等三角形的对应边相等). 在Rt△ABD和Rt△ABF中, {
????=????
????=????
∴Rt△ABD≌Rt△ABF(HL). ∴BD=BF(全等三角形的对应边相等). ∴BD-CD=BF-EF(等式的性质),即BC=BE
22.【答案】(1)证明:∵∠ACB=90°, ∴∠1+∠BCD=90°, ∵∠1=∠B, ∴∠B+∠BCD=90°, ∴∠BDC=90°, ∴CD⊥AB (2)解:∵S△ABC= /AB?CD= /AC?BC, ∴CD= /= /=4.8
23.【答案】(1)2或4;解:∠CDQ的大小不变
∵P、Q用时出发,速度相同,所以AP=BQ,
∵△ABC是等边三角形,
∴BA=AC,∠B=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠B=∠APC,BQ=AP,
∴△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∴∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°;
(2)解:如图4,
/
∠CDQ=120°,理由如下:
∵△ABC是等边三角形,
∴BA=AC,∠ABC=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠ABQ=∠CAP,BQ=AP,
∴△ABQ≌△CAP,
∴∠Q=∠P,
∵∠P+∠BCP=60°,
∴∠Q+∠DCQ=60°,
∴∠CDQ=120°.
一、单选题(共10题;共20分)
1.下列命题的逆命题正确的是(?? )
A.全等三角形的面积相等 B.全等三角形的周长相等 C.等腰三角形的两个底角相等 D.直角都相等
2.已知直角三角形ABC,有一个锐角等于50°,则另一个锐角的度数是(???? ).
A.?30°??????????????????????????????????????/B.?? 40°??????????????????????????????????????/C.?45°??????????????????????????????????????/D.?50°
3.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是(??? )
/
A.3.5 B.4.2 C.5.8 D.7
4.在下列条件:①∠A+∠B=∠C,②∠A∶∠B∶∠C=3∶4∶5,③∠C=∠A-∠B, ④a∶b∶c=3∶4∶5 中,能确定△ABC是直角三角形的条件有(????? )
A.1个 B.2个 C.3个 D.4个
5.下列命题中,逆命题不正确的是(?? )
A.?两直线平行,同旁内角互补????????????????????????????????/B.?直角三角形的两个锐角互余 C.?全等三角形对应角相等???????????????????????????????????????/D.?直角三角形斜边上的中线等于斜边的一半
6.如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都在图中的格点上,其中点A、点B的位置如图所示,则点C可能的位置共有( ??)
/
A.9个 B.8个 C.7个 D.6个
7.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是(?? ) /
A.?AB=A′B′=5,BC=B′C′=3???????????????????????????????/B.?AB=B′C′=5,∠A=∠B′=40° C.?AC=A′C′=5,BC=B′C′=3??????????????????????????????/D.?AC=A′C′=5,∠A=∠A′=40°
8.如图,AD是Rt△ABC斜边BC上的高,将△ACD沿AD所在的直线折叠,点C恰好落在BC的中点E处,则∠B等于(?? )
/
A.?25°???????????????????????????????????????B.?30°???????????????????????????????????????C.?45°???????????????????????????????????????D.?60°
9.若△ABC三边长a,b,c满足
??+???32
+ |b-a-2| + (c-8)2=0,则△ABC是(??? )
A.?等腰三角形????????????????????/B.?等边三角形????????????????????/C.?直角三角形????????????????????/D.?等腰直角三角形
10.如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为(??????? ).
/
A.?
7
4
????????????????????????????????/B.?1????????????????????????????????/C.?
7
4
或1或
9
4
????????????????????????????????/D.?
7
4
或1或
11
4
二、填空题(共7题;共7分)
11.命题“在同一个三角形中,等角对等边”的逆命题是________.
12.若一个三角形三边长分别为 1.5,2,2.5,则这个三角形一定是________三角形.
13.如图,山坡的倾斜角∠ABC为30°,小明沿山坡BA从山脚B点步行到山顶A共走了100m,则山顶的高度AC是________m.
/
14.用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是________.
15.如图,在△ABC中,∠ABC=90°,∠A=50°,CD=CB,∠ABD=________.
/
16.将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是________cm2/
17.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为
65
,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为
65
时,正方形EFGH的面积的所有可能值是________(不包括5).
/
三、解答题(共6题;共52分)
18.如图,△ABC中,AB=AC,D点在BC上,∠1=30°,且∠4=60°,
/
求证:
(1)AD=BD;
(2)CD=2BD.
19.如图,在△ABC中,∠BAC=∠ABC,点P在AB上,如果AD⊥CP,BE⊥CP的延长线,垂足分别为D,E,且BE=CD.
/
(1)试探求这个图形中还有哪些相等的线段,并给出证明;
(2)试确定△ABC的形状.
20.如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
/
21.如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE. /
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
22.如图所示,在△ACB中,∠ACB=90°,∠1=∠B. /
(1)求证:CD⊥AB;
(2)如果AC=8,BC=6,AB=10,求CD的长.
23.边长为6的等边△ABC中,点P从点A出发沿射线AB方向移动,同时点Q从点B出发,以相同的速度沿射线BC方向移动,连接AQ、CP,直线AQ、CP相交于点D.
/??? /
(1)如图①,当点P、Q分别在边AB、BC上时,
①连接PQ,当△BPQ是直角三角形时,AP等于________;
②∠CDQ的大小是否随P,Q的运动而变化?如果不会,请求出∠CDQ的度数;如果会,请说明理由;________
(2)当P、Q分别在边AB、BC的延长线上时,在图②中画出点D,并直接写出∠CDQ的度数.
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】在同一个三角形中,等边对等角
12.【答案】直角
13.【答案】50
14.【答案】/a<b<a
15.【答案】20°
16.【答案】2
17.【答案】9或13或49
三、解答题
18.【答案】(1)证明:∵∠4=60°,∠1=30°,
∴∠ABD=∠4-∠1=60°-30°=30°=∠1.
∴BD=AD
(2)证明:∵∠ABD=30°,
又∵AB=AC,
∴∠C=∠ABD=30°,
∴∠2=180°-∠4-∠C=180°-60°-30°=90°,
∵∠C=30°,
∴CD=2AD=2BD
19.【答案】(1)解:图中相等的线段还有AC=BC,CE=AD.
证明:∵∠BAC=∠ABC, ∴AC=BC.
∵AD⊥CP,BE⊥CP,
∴∠ADC=∠BEC=90°.
又∵BE=CD,
∴Rt△BCE≌Rt△CAD(HL).???????
∴CE=AD 。
(2)解:△ABC为等腰直角三角形,理由如下 : ∵△BCE≌△CAD,
∴∠EBC=∠ACD.
∵∠EBC+∠BCE=90°,
∴∠ACD+∠BCE=90°,即∠ACB=90°. 又AC=BC ,
∴△ABC为等腰直角三角形 。
20.【答案】解:连接BD
/
在Rt△ABD中,BD2=AB2+AD2=32+42=52 ,
在△CBD中,CD2=132 , BC2=122 , 而122+52=132 , 即BC2+BD2=CD2 ,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=
1
2
AD·AB+
1
2
DB· BC=
1
2
×4×3+
1
2
×5×12=36
所以需费用36×200=7200(元)
21.【答案】(1)解:画出高AD,AF,如图所示./ (2)解:猜想:BC=BE.证明如下: ∵AD⊥BC,AF⊥BE, ∴△ACD,△AEF,△ABD,△ABF都是直角三角形. 在Rt△ACD和Rt△AEF中, {
????=????
????=????
∴Rt△ACD≌Rt△AEF(HL). ∴CD=EF(全等三角形的对应边相等). 在Rt△ABD和Rt△ABF中, {
????=????
????=????
∴Rt△ABD≌Rt△ABF(HL). ∴BD=BF(全等三角形的对应边相等). ∴BD-CD=BF-EF(等式的性质),即BC=BE
22.【答案】(1)证明:∵∠ACB=90°, ∴∠1+∠BCD=90°, ∵∠1=∠B, ∴∠B+∠BCD=90°, ∴∠BDC=90°, ∴CD⊥AB (2)解:∵S△ABC= /AB?CD= /AC?BC, ∴CD= /= /=4.8
23.【答案】(1)2或4;解:∠CDQ的大小不变
∵P、Q用时出发,速度相同,所以AP=BQ,
∵△ABC是等边三角形,
∴BA=AC,∠B=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠B=∠APC,BQ=AP,
∴△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∴∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°;
(2)解:如图4,
/
∠CDQ=120°,理由如下:
∵△ABC是等边三角形,
∴BA=AC,∠ABC=∠CAP=60°,
在△ABQ和△CAP中,
BA=AC,∠ABQ=∠CAP,BQ=AP,
∴△ABQ≌△CAP,
∴∠Q=∠P,
∵∠P+∠BCP=60°,
∴∠Q+∠DCQ=60°,
∴∠CDQ=120°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
