苏教版选修2-1课件: 3.2.2 空间线面关系的判定 课件(34张)
文档属性
| 名称 | 苏教版选修2-1课件: 3.2.2 空间线面关系的判定 课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 614.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-02 16:47:33 | ||
图片预览




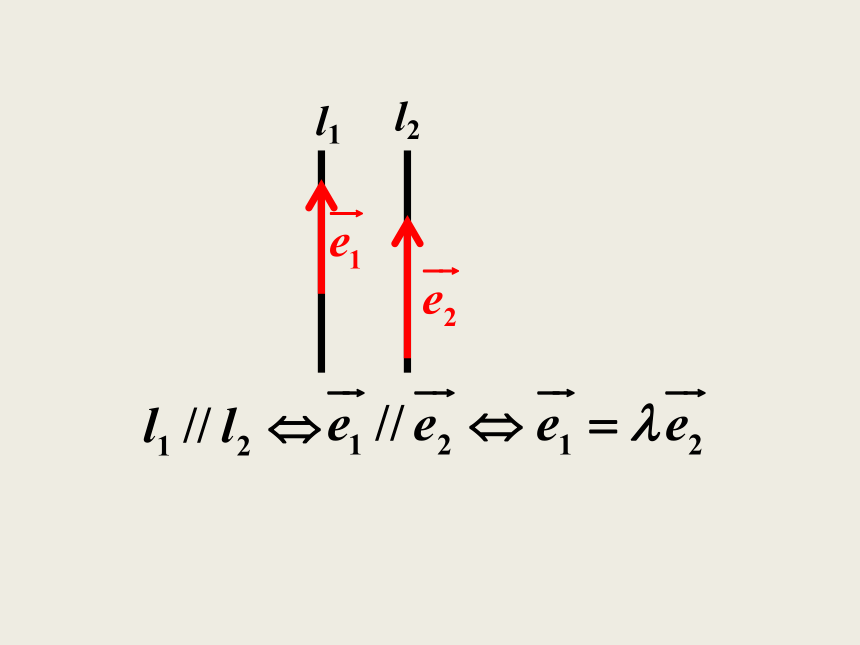
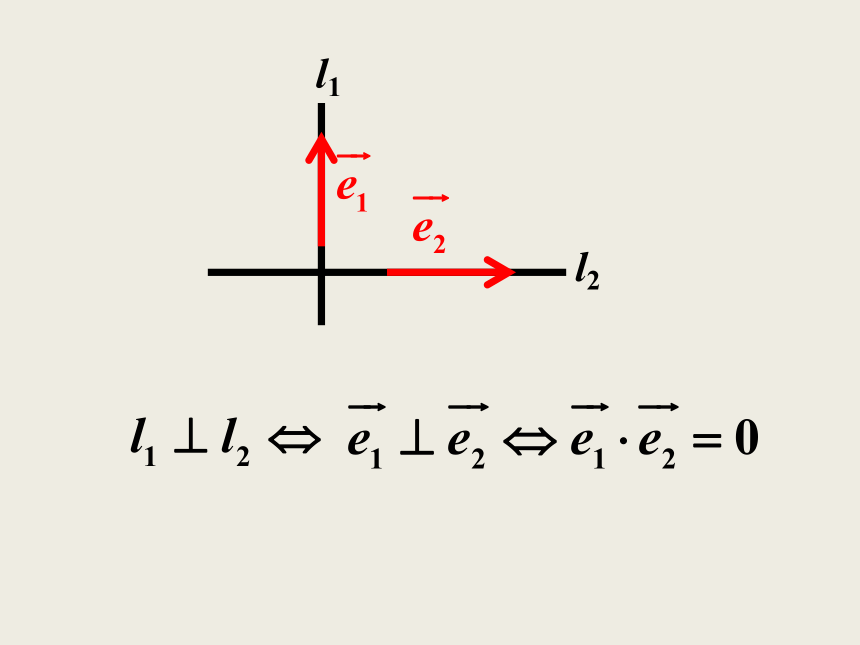
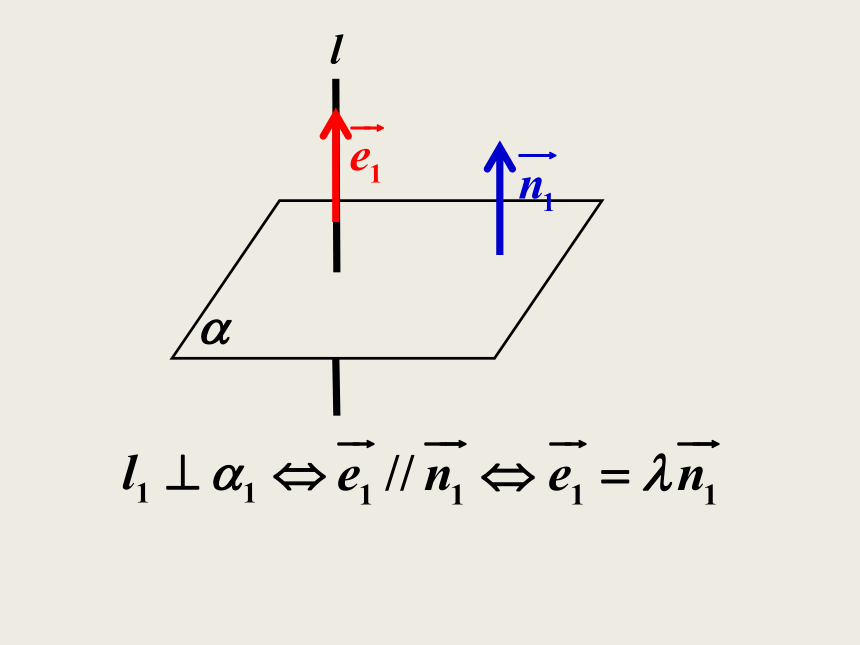
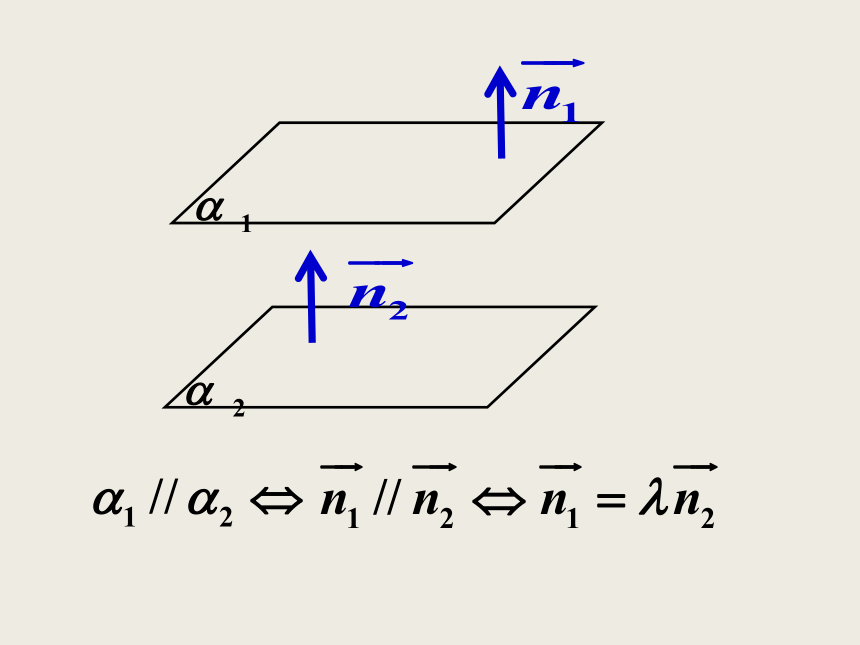
文档简介
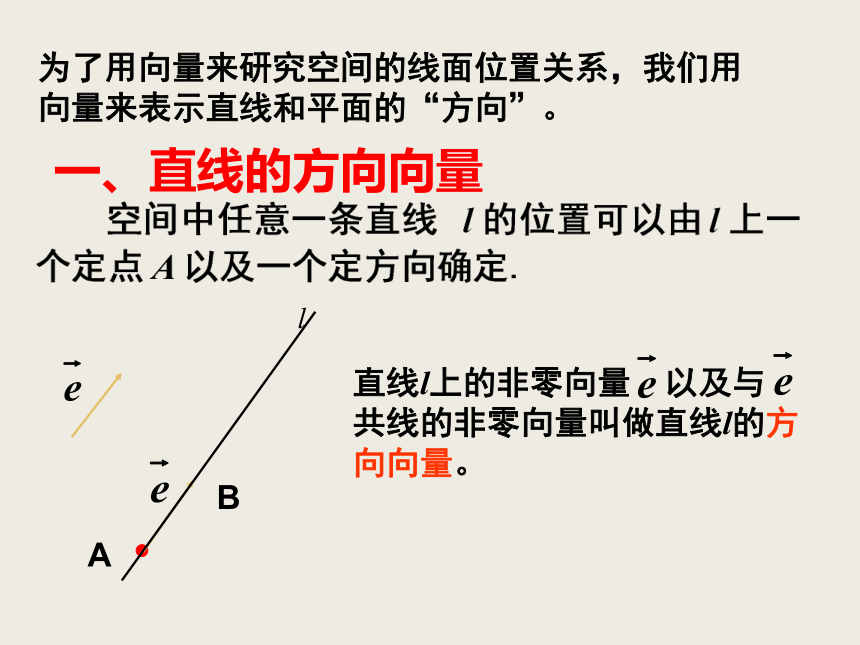
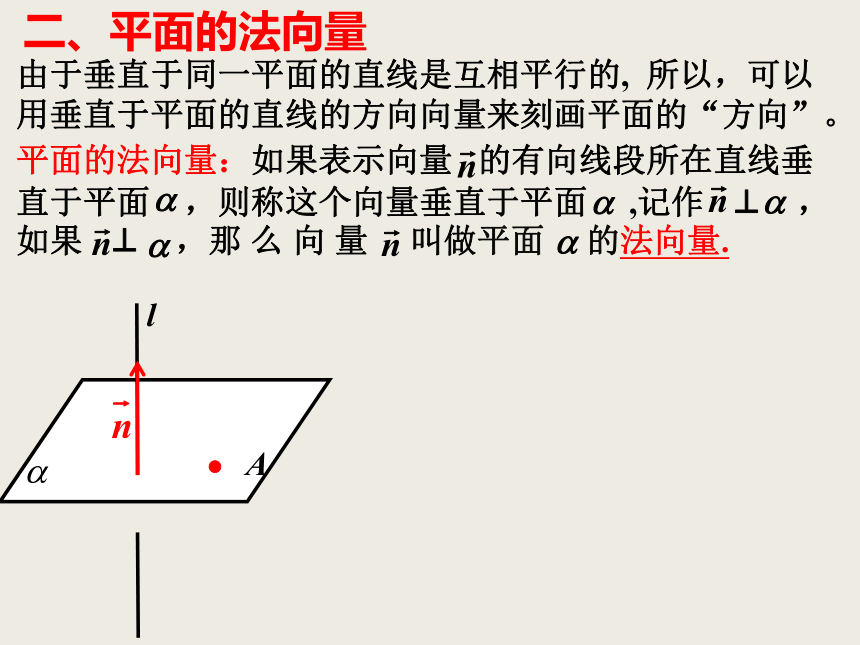
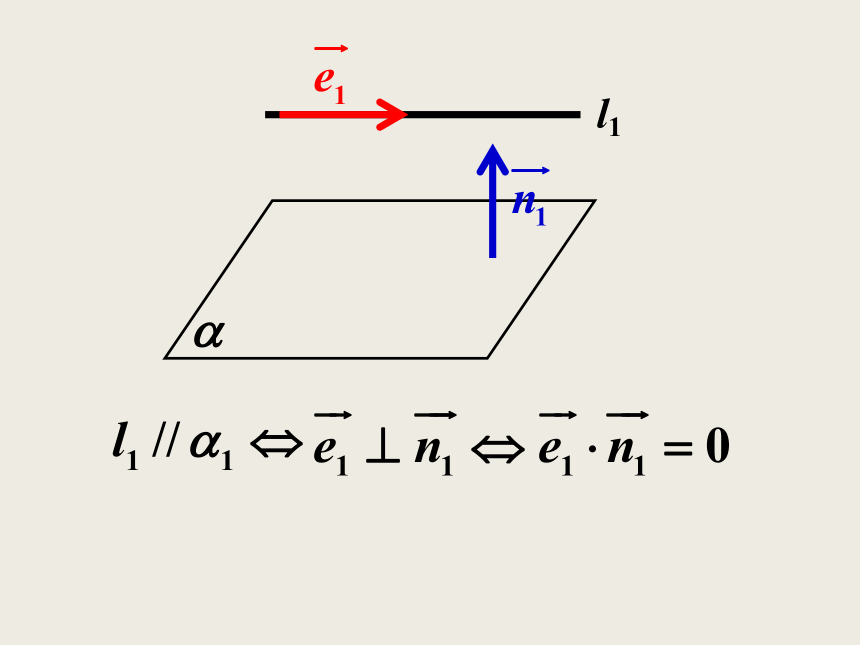
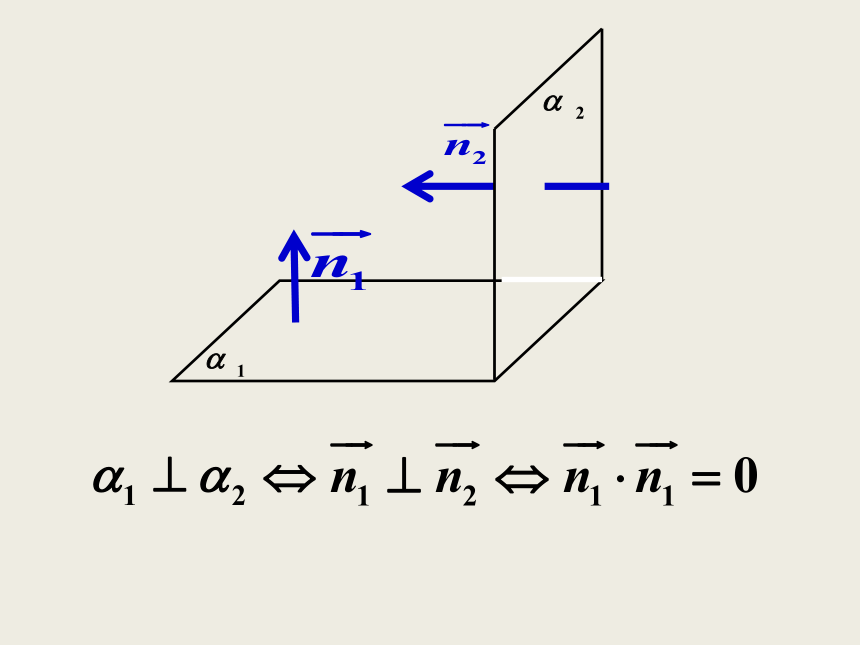
课件34张PPT。问题情境 在“立体几何初步”一章中,我们研究了空间两条直线、直线与平面、平面与平面的位置关系.为了用向量来研究空间的线面位置关系,我们用向量来表示直线和平面的“方向”。一、直线的方向向量直线l上的非零向量 以及与 共线的非零向量叫做直线l的方向向量。由于垂直于同一平面的直线是互相平行的, 所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。二、平面的法向量平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.l思考: 我们能不能用直线的方向
向量和平面法向量来刻画空间线
面位置关系?空间线面关系的判定学生活动l1l2l1l2l1l 设空间两条直线 的方向向量为
两个平面 的法向量分别为建构数学1.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.平行垂直平行新知巩固新知巩固2.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交新知巩固3、设平面 的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若 ,则k= ;若 则 k= 。4-5-85、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ,则m= .44、已知 ,且 的方向向量为(2,m,1),平面 的法向量为(1,1/2,2),则m= . 例1、如图, 是平面 的一条斜线, 为斜足, , 为垂足, ,且
求证:
在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。(三垂线定理)数学应用变式练习:
写出三垂线定理的逆定理,并用向量的方法加以证明。
三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。 三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直。OBDCA已知:如图, 是平面 的 一条斜线, 为斜足, , 为垂足,
,且
求证:
例2、证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面。(直线与平面垂直的判定定理)已知:如图,
求证:
分析:要证明直线与平面垂直,只要证明该直线垂直于平面内任意一条直线。相交不共线又共面存在有序实数组使得,例3、如图,在直三棱柱 - 中,
是棱 的中点,
求证:
证明:在直三棱柱 - 中,
因为 ,所以
因为 ,而
所以 ,所以
在 中,因为
所以所以
因为 , ,
且 是棱 中点,所以 ,
所以 思考:还有其它的证明方法吗?
启示:
1、要确定方向:证明垂直关系,可通过向量的数量积等于0来实现。
2、要善于转化,即挖掘已知的向量的关系,将未知向已知转化。利用相似三角形与线面垂直分析:连结 交 于点
因为
所以,要证
就是证
即证
1、利用 相似可以证明 ,
从而2、利用 知道 ,即 你能试着建立适当的空间直角坐标系,用坐标表示向量,再证明它们互相垂直吗?证明:分别以
所在直线为 轴, 轴, 轴,建
立空间直角坐标系图中相应点的坐标为:所以:所以:即,三种方法的比较:
证法一是几何向量法,要熟练掌握向量的加减运算及所满足的运算律。
证法二是几何向量法和立体几何法的综合运用。
证法三是向量的坐标运算法,关键是要恰当地建立空间直角坐标系,探求出各点的坐标。 最终都是应用向量的数量积为0来证明线线垂直。思考:
(1)请证明:(2)请证明:回顾小结本节课学习了以下内容:
1.学会用向量语言表述线线、线面、面面的平行和垂直关系;
2.学会用向量方法证明空间线面关系的一些定理;
3.学会用向量方法判定空间线面的垂直关系.谢谢指导
向量和平面法向量来刻画空间线
面位置关系?空间线面关系的判定学生活动l1l2l1l2l1l 设空间两条直线 的方向向量为
两个平面 的法向量分别为建构数学1.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.平行垂直平行新知巩固新知巩固2.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交新知巩固3、设平面 的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若 ,则k= ;若 则 k= 。4-5-85、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ,则m= .44、已知 ,且 的方向向量为(2,m,1),平面 的法向量为(1,1/2,2),则m= . 例1、如图, 是平面 的一条斜线, 为斜足, , 为垂足, ,且
求证:
在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。(三垂线定理)数学应用变式练习:
写出三垂线定理的逆定理,并用向量的方法加以证明。
三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。 三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直。OBDCA已知:如图, 是平面 的 一条斜线, 为斜足, , 为垂足,
,且
求证:
例2、证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面。(直线与平面垂直的判定定理)已知:如图,
求证:
分析:要证明直线与平面垂直,只要证明该直线垂直于平面内任意一条直线。相交不共线又共面存在有序实数组使得,例3、如图,在直三棱柱 - 中,
是棱 的中点,
求证:
证明:在直三棱柱 - 中,
因为 ,所以
因为 ,而
所以 ,所以
在 中,因为
所以所以
因为 , ,
且 是棱 中点,所以 ,
所以 思考:还有其它的证明方法吗?
启示:
1、要确定方向:证明垂直关系,可通过向量的数量积等于0来实现。
2、要善于转化,即挖掘已知的向量的关系,将未知向已知转化。利用相似三角形与线面垂直分析:连结 交 于点
因为
所以,要证
就是证
即证
1、利用 相似可以证明 ,
从而2、利用 知道 ,即 你能试着建立适当的空间直角坐标系,用坐标表示向量,再证明它们互相垂直吗?证明:分别以
所在直线为 轴, 轴, 轴,建
立空间直角坐标系图中相应点的坐标为:所以:所以:即,三种方法的比较:
证法一是几何向量法,要熟练掌握向量的加减运算及所满足的运算律。
证法二是几何向量法和立体几何法的综合运用。
证法三是向量的坐标运算法,关键是要恰当地建立空间直角坐标系,探求出各点的坐标。 最终都是应用向量的数量积为0来证明线线垂直。思考:
(1)请证明:(2)请证明:回顾小结本节课学习了以下内容:
1.学会用向量语言表述线线、线面、面面的平行和垂直关系;
2.学会用向量方法证明空间线面关系的一些定理;
3.学会用向量方法判定空间线面的垂直关系.谢谢指导
