苏教版选修2-1课件: 3.1.1 空间向量及其线性运算 课件(20张)
文档属性
| 名称 | 苏教版选修2-1课件: 3.1.1 空间向量及其线性运算 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 720.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-02 16:42:10 | ||
图片预览







文档简介
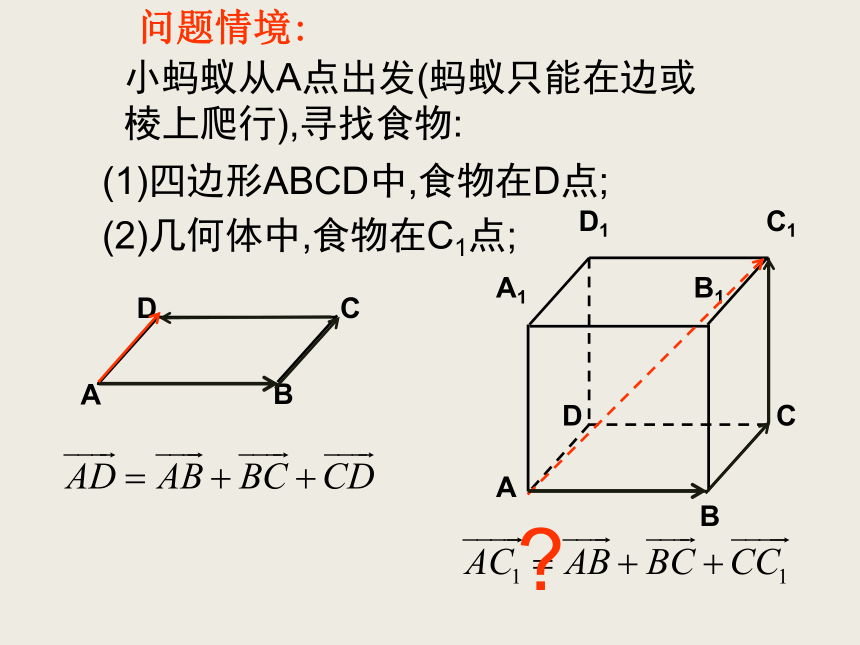
课件20张PPT。ADC1小蚂蚁从A点出发(蚂蚁只能在边或棱上爬行),寻找食物:问题情境:ABCD(1)四边形ABCD中,食物在D点;(2)几何体中,食物在C1点;?空间向量
及其线性运算想一想:温故:知识再现:平面向量1、定义:既有大小又有方向的量。2、几何表示法:3、相等向量:长度相等且方向相同的向量用小写字母 表示,或者用表示向量的
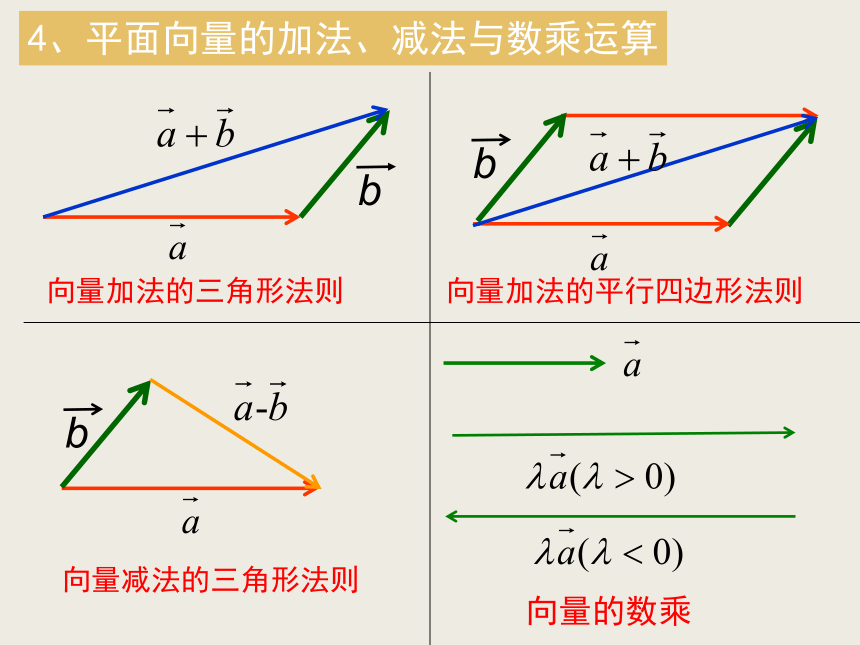
有向线段的起点和终点字母表示。用有向线段表示字母表示法:相反向量:长度相等且方向相反的向量4、平面向量的加法、减法与数乘运算向量加法的三角形法则向量减法的三角形法则5、平面向量的加法、减法与数乘运算律6、平面共线(平行)向量的定义方向相同或相反的非零向量叫做平行向量
又称共线向量7、平面向量共线定理知新:1.空间向量的表示:(1)在空间中,把象位移、力、速度、加速度这样既有大小又有方向的量,叫做空间向量。(2)空间向量和平面向量一样,空间向量也用有向线段表示.凡是方向相同且长度相等的有向线段都表示同一向量或相等向量.凡是方向相反且长度相等的有向线段都表示相反向量.问题1:空间两条直线有几种位置关系?
问题2:空间两向量有几种位置关系?异面?平行、相交、异面2.对于任意两个空间向量 ,在空间任取一点O,作AB空间任意两个向量,都可以用某一平面内的两条有向线段表示.因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。与平面向量一样,空间向量的加法,减法,数乘运算的意义与平面向量运算的意义相同.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘: 为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律成立吗?数乘: 为正数,负数,零3. 空间向量的加法结合律成立吗?OABCOABC6.如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量称为平行向量或共线向量.记作:规定:零向量与任一向量共线.对于空间任意两个向量 , 共线
的充要条件是:存在实数 ,使得思考1:当实数 时, 表示什么意思?
思考2:充要条件中为什么规定7.概念认识:判断命题的真假:(1)两个空间向量相等,则它们的起点相同,终点也相同.(2)由 ,知 与 方向相同.(3)不相等的两个空间向量的模必不相等.(4)若空间向量 , , 满足 = , = 则 = .(5)若空间向量 , , 满足 , 则 . (6)空间中任意两个单位向量相等.(7)将所有单位向量的起点平移到同一点为起点,则它们终点的轨迹为单位圆.假假假真假假假1. 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式.例题讲解:2. 如图,在空间四边形ABCD中,E是AB中点,CF=2DF,化简下列各式:即学即练:2. 如图,在长方体OADB-CA1D1B1中,OA=3,
OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,
D1B1的中点,设 ,试用
表示下列向量.FE例题讲解:即学即练:小结
有向线段的起点和终点字母表示。用有向线段表示字母表示法:相反向量:长度相等且方向相反的向量4、平面向量的加法、减法与数乘运算向量加法的三角形法则向量减法的三角形法则5、平面向量的加法、减法与数乘运算律6、平面共线(平行)向量的定义方向相同或相反的非零向量叫做平行向量
又称共线向量7、平面向量共线定理知新:1.空间向量的表示:(1)在空间中,把象位移、力、速度、加速度这样既有大小又有方向的量,叫做空间向量。(2)空间向量和平面向量一样,空间向量也用有向线段表示.凡是方向相同且长度相等的有向线段都表示同一向量或相等向量.凡是方向相反且长度相等的有向线段都表示相反向量.问题1:空间两条直线有几种位置关系?
问题2:空间两向量有几种位置关系?异面?平行、相交、异面2.对于任意两个空间向量 ,在空间任取一点O,作AB空间任意两个向量,都可以用某一平面内的两条有向线段表示.因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。与平面向量一样,空间向量的加法,减法,数乘运算的意义与平面向量运算的意义相同.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘: 为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律成立吗?数乘: 为正数,负数,零3. 空间向量的加法结合律成立吗?OABCOABC6.如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量称为平行向量或共线向量.记作:规定:零向量与任一向量共线.对于空间任意两个向量 , 共线
的充要条件是:存在实数 ,使得思考1:当实数 时, 表示什么意思?
思考2:充要条件中为什么规定7.概念认识:判断命题的真假:(1)两个空间向量相等,则它们的起点相同,终点也相同.(2)由 ,知 与 方向相同.(3)不相等的两个空间向量的模必不相等.(4)若空间向量 , , 满足 = , = 则 = .(5)若空间向量 , , 满足 , 则 . (6)空间中任意两个单位向量相等.(7)将所有单位向量的起点平移到同一点为起点,则它们终点的轨迹为单位圆.假假假真假假假1. 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式.例题讲解:2. 如图,在空间四边形ABCD中,E是AB中点,CF=2DF,化简下列各式:即学即练:2. 如图,在长方体OADB-CA1D1B1中,OA=3,
OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,
D1B1的中点,设 ,试用
表示下列向量.FE例题讲解:即学即练:小结
