苏教版选修2-1课件: 3.1.5 空间向量的数量积 课件(44张)
文档属性
| 名称 | 苏教版选修2-1课件: 3.1.5 空间向量的数量积 课件(44张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-02 16:46:26 | ||
图片预览










文档简介
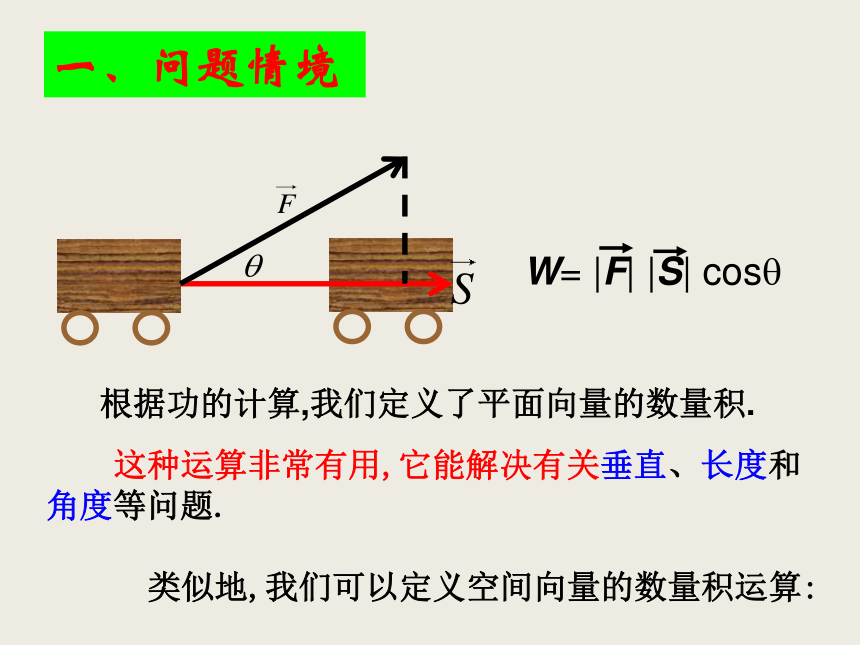
课件44张PPT。空间向量的数量积 根据功的计算,我们定义了平面向量的数量积. 类似地,我们可以定义空间向量的数量积运算: 这种运算非常有用,它能解决有关垂直、长度和
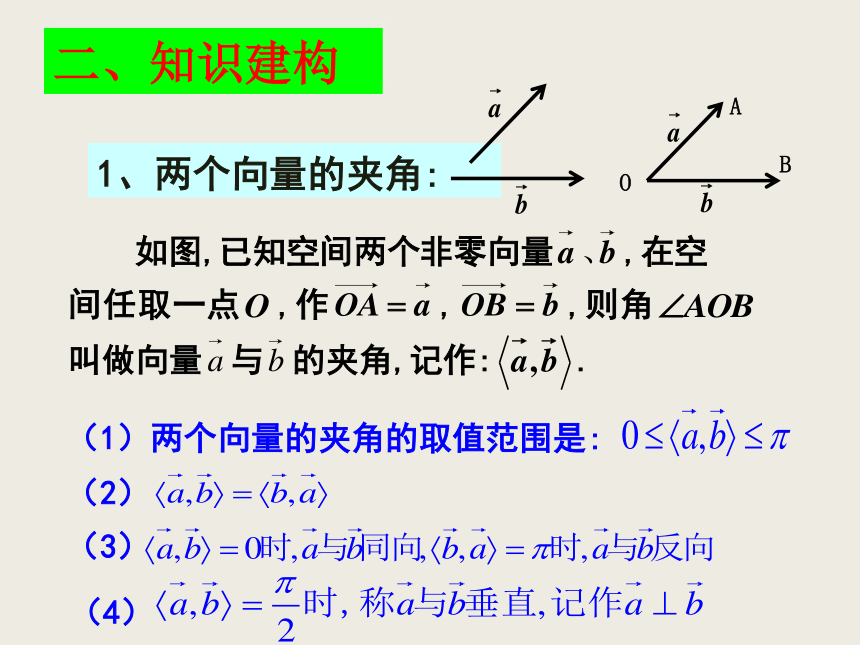
角度等问题.一、问题情境1、两个向量的夹角:(1)两个向量的夹角的取值范围是:(2)(3)(4)二、知识建构 2、两个向量的数量积(1)两个向量的数量积是数量,而不是向量.(2)规定:零向量与任意向量的数量积等于零.注意: 性质(1)是证明两向量垂直的依据;
性质(2)是求向量的长度(模)的依据;
性质(3)是求向量的夹角的依据. 3、空间两个向量的数量积性质(3)空间两个非零向量 的夹角 满足: 4、空间向量的数量积满足的运算律思考:吗?(2)对于向量 , 成立吗? 5、空间向量的数量积的坐标表示问题2令 , 可以得出怎样的结果?模长公式问题1 平面向量的数量积可以用坐标表示,空间向量的数量积能用坐标表示吗?怎样表示呢?问题3若 , 则能得出怎样的结论?向量垂直充要条件的坐标表示问题4两空间向量夹角的余弦值能用坐标表示吗? 例1、已知空间向量 满足
试求: 变式 向量 求:三、数学应用 变式1 空间四边形OABC中,
且OA=OB=OC,M、N分别是OA、BC的中点,G是MN的中点,求 . 变式2 已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB. 例3、 已知m,n是平面?内的两条相交直线,直线 l 满足:l⊥m,l⊥n,求证:l⊥?.
解:由 ,可知 .
由 ,知
.例5 已知在平行六面体 中, ,
,
求对角线 的长.解:例6 已知 、 ,求:
(1)线段 的中点坐标和长度; 解:设 是 的中点,则∴点 的坐标是 . 例6 已知 、 ,求:
(3)设O为坐标原点,求 的面积. (2)到 两点距离相等的点 的
坐标 满足的条件.解:点 到 的距离相等,则化简整理,得即到 两点距离相等的点的坐标 满
足的条件是 例7 已知点A ( 1 , 0 , 0 ) , B ( 0 , 1 , 0 ), C ( 0 , 0 , 1 ) , 求满足下列条件的点D的坐标: (1) DB∥AC且DC ∥AB; (2) DB AC , DC AB且AD=BC. 变式 已知A ( 1 , -1 , ,7 ) , B ( 3 , -2 , 5 ), C ( 2 , -3 , 9 ) , 求: 三角形ABC的各边之长和各内角的大小. 解:设正方体的棱长为1,如图建立空间直角坐标系 ,则: 例8 如图,在正方体ABCD-A1B1C1D1中,点E1、F1分别是A1B1、C1D1的一个四等分点,求BE1与DF1所成的角的余弦值. 变式1C1B1A1D1DABCMP 如图,在正方体ABCD-A1B1C1D1中,点Q是AD的中点,点P是C1B1的中点,求A1P与DQ所成角的余弦值. 所求的余弦值为 .FEC1B1A1D1DABC变式2 如图,在正方体ABCD-A1B1C1D1中,点E、F分别是BB1、D1B1的一个中点,求证: EF与DA1互相垂直.1.已知线段 、 在平面 内, ,线段
,如果 ,求 、 之间的距离.解:∵四、巩固练习2.已知空间四边形 的每条边和对角线的长都等于
,点 分别是边 的中点.
求证: .同理,3.已知空间四边形
,求证: .证明:∵4.如图,已知正方体 , 和 相交于
点 ,连结 ,求证: . 6.已知空间四边形 的每条边和对角线的长都等于 ,点 分别是 的中点,求下列向量的数量积:16.已知三角形ABC是正三角形,PA与平面ABC垂直,
求PB与AC所成的角的大小. 五、课堂小结1、空间向量的数量积:2、空间向量的数量积的应用.(1)定义;(2)性质;(3)坐标表示.(1)证明线线垂直;(2)求线段的长;(3)求线线夹角.再见!再见!再见!
角度等问题.一、问题情境1、两个向量的夹角:(1)两个向量的夹角的取值范围是:(2)(3)(4)二、知识建构 2、两个向量的数量积(1)两个向量的数量积是数量,而不是向量.(2)规定:零向量与任意向量的数量积等于零.注意: 性质(1)是证明两向量垂直的依据;
性质(2)是求向量的长度(模)的依据;
性质(3)是求向量的夹角的依据. 3、空间两个向量的数量积性质(3)空间两个非零向量 的夹角 满足: 4、空间向量的数量积满足的运算律思考:吗?(2)对于向量 , 成立吗? 5、空间向量的数量积的坐标表示问题2令 , 可以得出怎样的结果?模长公式问题1 平面向量的数量积可以用坐标表示,空间向量的数量积能用坐标表示吗?怎样表示呢?问题3若 , 则能得出怎样的结论?向量垂直充要条件的坐标表示问题4两空间向量夹角的余弦值能用坐标表示吗? 例1、已知空间向量 满足
试求: 变式 向量 求:三、数学应用 变式1 空间四边形OABC中,
且OA=OB=OC,M、N分别是OA、BC的中点,G是MN的中点,求 . 变式2 已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB. 例3、 已知m,n是平面?内的两条相交直线,直线 l 满足:l⊥m,l⊥n,求证:l⊥?.
解:由 ,可知 .
由 ,知
.例5 已知在平行六面体 中, ,
,
求对角线 的长.解:例6 已知 、 ,求:
(1)线段 的中点坐标和长度; 解:设 是 的中点,则∴点 的坐标是 . 例6 已知 、 ,求:
(3)设O为坐标原点,求 的面积. (2)到 两点距离相等的点 的
坐标 满足的条件.解:点 到 的距离相等,则化简整理,得即到 两点距离相等的点的坐标 满
足的条件是 例7 已知点A ( 1 , 0 , 0 ) , B ( 0 , 1 , 0 ), C ( 0 , 0 , 1 ) , 求满足下列条件的点D的坐标: (1) DB∥AC且DC ∥AB; (2) DB AC , DC AB且AD=BC. 变式 已知A ( 1 , -1 , ,7 ) , B ( 3 , -2 , 5 ), C ( 2 , -3 , 9 ) , 求: 三角形ABC的各边之长和各内角的大小. 解:设正方体的棱长为1,如图建立空间直角坐标系 ,则: 例8 如图,在正方体ABCD-A1B1C1D1中,点E1、F1分别是A1B1、C1D1的一个四等分点,求BE1与DF1所成的角的余弦值. 变式1C1B1A1D1DABCMP 如图,在正方体ABCD-A1B1C1D1中,点Q是AD的中点,点P是C1B1的中点,求A1P与DQ所成角的余弦值. 所求的余弦值为 .FEC1B1A1D1DABC变式2 如图,在正方体ABCD-A1B1C1D1中,点E、F分别是BB1、D1B1的一个中点,求证: EF与DA1互相垂直.1.已知线段 、 在平面 内, ,线段
,如果 ,求 、 之间的距离.解:∵四、巩固练习2.已知空间四边形 的每条边和对角线的长都等于
,点 分别是边 的中点.
求证: .同理,3.已知空间四边形
,求证: .证明:∵4.如图,已知正方体 , 和 相交于
点 ,连结 ,求证: . 6.已知空间四边形 的每条边和对角线的长都等于 ,点 分别是 的中点,求下列向量的数量积:16.已知三角形ABC是正三角形,PA与平面ABC垂直,
求PB与AC所成的角的大小. 五、课堂小结1、空间向量的数量积:2、空间向量的数量积的应用.(1)定义;(2)性质;(3)坐标表示.(1)证明线线垂直;(2)求线段的长;(3)求线线夹角.再见!再见!再见!
