数学苏教版选修1-1课件: 1.1.2 充分条件与必要条件 课件(21张)
文档属性
| 名称 | 数学苏教版选修1-1课件: 1.1.2 充分条件与必要条件 课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 181.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-03 00:00:00 | ||
图片预览








文档简介
课件21张PPT。充分条件
和必要条件
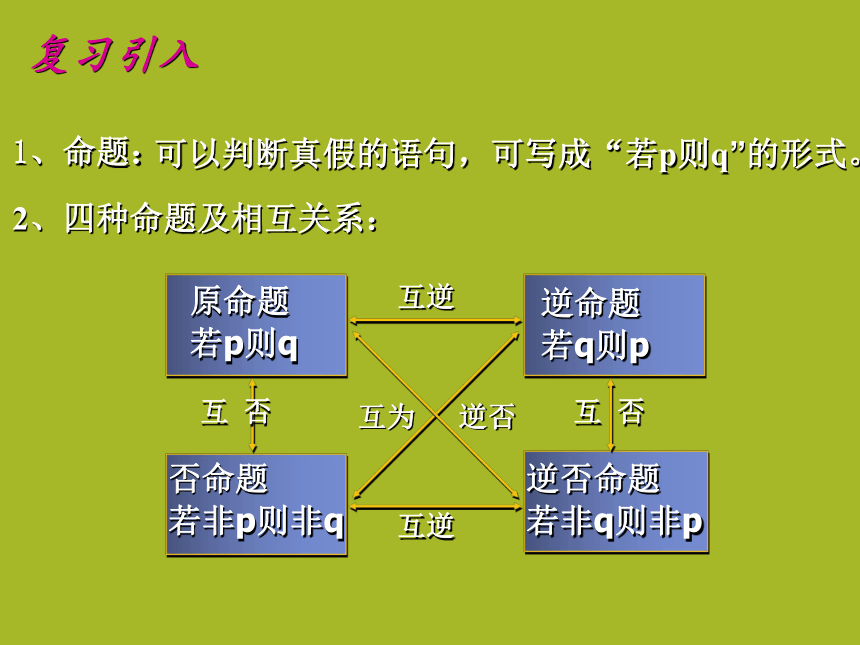
(一)1、命题:可以判断真假的语句,可写成“若p则q”的形式。 2、四种命题及相互关系:复习引入判断下列命题是真命题还是假命题。 1)若x=y,则x2=y2。 2)有两角相等的三角形是等腰三角形。 3)若a∈R,则a ∈ Q。 4)若一个数可以被5整除,则它的末位是0.假命题假命题真命题在真命题(1)和(2)中,条件足以推导出结论, 也就是说条件充分了。 在假命题(3)和(4)中条件不充分。真命题复习引入 如果命题“若p则q”为真,则记作p q。如果命题“若p则q”为假,则记作p q。定义:如果 ,则称p是q的充分条件,
同时称q是p的必要条件。新课思考:你能举例说出p是q的充分条件吗?解:命题(1)(2)是真命题( ),
命题(3)是假命题( ),
所以,命题(1)(2)中的p是q的充分条件.例1.下列“若p则q”形式的命题中,哪些命题中的
p是q的充分条件?
(1)若 x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数 .概念应用例2.下列“若p则q”形式的命题中,哪些命题中的
q是p的必要条件?
(1)若 x3=y3,则x=y;
(2)若两个三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc.
解:命题(1)(2)是真命题( ),
命题(3)是假命题( ),
所以,命题(1)(2)中的q是p的必要条件.
概念应用以下四句话
1) 命题“若p则q”是真命题
2) p q 3) p是q的充分条件 4) q是p的必要条件定义:如果 ,则称p是q的充分条件,
同时称q是p的必要条件。表达的是同一逻辑关系,只是说法不同。 新课判断下列命题是真命题还是假命题。 1)若x=y,则x2=y2。 2)有两角相等的三角形是等腰三角形。 3)若a∈R,则a ∈ Q。 4)若一个数可以被5整除,则它的末位是0.假命题假命题真命题在真命题(1)、(2)中,条件足以导出结论, 也就是说条件充分了。 在假命题(3)、(4)中条件不充分。真命题复习引入指出以下各题中p是q的什么条件,q是p的什么条件? 1)p: x=y,q: x2=y2。 2)p: 三角形有两个角相等,q: 它是等腰三角形。 3)p: a∈R,q: a∈Q。 4)p: 实数x可以被5整除,q: 实数x的末位是0.p是q的充分条件, q是p的必要条件p是q的充分条件,也是q的必要条件
q是p的充分条件,也是p的必要条件p是q的必要条件, q是p的充分条件p是q的必要条件, q是p的充分条件温故知新定义:数学建构定义:数学建构1、看p能否推出q,即判断命题“若p则q”的真假思考:要判断p是q的什么条件,需要经过哪些步骤?数学建构2、看q能否推出p,即判断命题“若q则p”的真假3、由1和2,根据定义得出p是q什么条件 例3.指出下列命题中, p是q的什么条件.(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分又不必要条件”中选出一种)
(1) p: x-1=0,q:( x-1)(x+2)=0;
(2) p:两直线平行, q:内错角相等;
(3) p:a>b,q:a2>b2 ;
(4) p:四边形的四条边相等,q:四边形是正方形.知识运用 练习1.以“充分不必要条件”、“必要不充分条件”、“充要条件”与”既不充分也不必要条件“中选出适当的一种填空.充分不必要条件必要不充分条件必要不充分条件充分不必要条件充要条件充要条件既不充分又不必要条件练习2.已知A是B的必要而不充分条件,C是B的充要
条件,D是C的充分而不必要条件,那么D是A的
条件。例4.已知p,q都是r的必要条件,s是r的充分条件,
q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?练习3.已知p是q的必要而不充分条件,
那么非q是非p的_______________条件.充分不必要变式.非A是非B的充分不必要条件,非C是非B的
充要条件, 则A是C的 条件
必要不充分例5. 已知命题p: ,
命题q: ,
若p是q的必要不充分条件,求实数m的取值范围。一.定义:课堂小结二.判别步骤:① 认清条件和结论。② 考察p q和q p的真假。(2)从定义出发:
首先分清条件和结论,然后运用定义来判断.三.判别的常用方法:(3)从集合的角度出发:
由两个集合之间的包含关系来判断 (1)从命题的角度出发:
原命题“若p则q”或逆否命题(若非q则非p)为真,
就说明p是q的充分条件.1.学案:课后检测
2.预习《充分条件和必要条件(二)》课后作业谢谢!
和必要条件
(一)1、命题:可以判断真假的语句,可写成“若p则q”的形式。 2、四种命题及相互关系:复习引入判断下列命题是真命题还是假命题。 1)若x=y,则x2=y2。 2)有两角相等的三角形是等腰三角形。 3)若a∈R,则a ∈ Q。 4)若一个数可以被5整除,则它的末位是0.假命题假命题真命题在真命题(1)和(2)中,条件足以推导出结论, 也就是说条件充分了。 在假命题(3)和(4)中条件不充分。真命题复习引入 如果命题“若p则q”为真,则记作p q。如果命题“若p则q”为假,则记作p q。定义:如果 ,则称p是q的充分条件,
同时称q是p的必要条件。新课思考:你能举例说出p是q的充分条件吗?解:命题(1)(2)是真命题( ),
命题(3)是假命题( ),
所以,命题(1)(2)中的p是q的充分条件.例1.下列“若p则q”形式的命题中,哪些命题中的
p是q的充分条件?
(1)若 x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数 .概念应用例2.下列“若p则q”形式的命题中,哪些命题中的
q是p的必要条件?
(1)若 x3=y3,则x=y;
(2)若两个三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc.
解:命题(1)(2)是真命题( ),
命题(3)是假命题( ),
所以,命题(1)(2)中的q是p的必要条件.
概念应用以下四句话
1) 命题“若p则q”是真命题
2) p q 3) p是q的充分条件 4) q是p的必要条件定义:如果 ,则称p是q的充分条件,
同时称q是p的必要条件。表达的是同一逻辑关系,只是说法不同。 新课判断下列命题是真命题还是假命题。 1)若x=y,则x2=y2。 2)有两角相等的三角形是等腰三角形。 3)若a∈R,则a ∈ Q。 4)若一个数可以被5整除,则它的末位是0.假命题假命题真命题在真命题(1)、(2)中,条件足以导出结论, 也就是说条件充分了。 在假命题(3)、(4)中条件不充分。真命题复习引入指出以下各题中p是q的什么条件,q是p的什么条件? 1)p: x=y,q: x2=y2。 2)p: 三角形有两个角相等,q: 它是等腰三角形。 3)p: a∈R,q: a∈Q。 4)p: 实数x可以被5整除,q: 实数x的末位是0.p是q的充分条件, q是p的必要条件p是q的充分条件,也是q的必要条件
q是p的充分条件,也是p的必要条件p是q的必要条件, q是p的充分条件p是q的必要条件, q是p的充分条件温故知新定义:数学建构定义:数学建构1、看p能否推出q,即判断命题“若p则q”的真假思考:要判断p是q的什么条件,需要经过哪些步骤?数学建构2、看q能否推出p,即判断命题“若q则p”的真假3、由1和2,根据定义得出p是q什么条件 例3.指出下列命题中, p是q的什么条件.(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分又不必要条件”中选出一种)
(1) p: x-1=0,q:( x-1)(x+2)=0;
(2) p:两直线平行, q:内错角相等;
(3) p:a>b,q:a2>b2 ;
(4) p:四边形的四条边相等,q:四边形是正方形.知识运用 练习1.以“充分不必要条件”、“必要不充分条件”、“充要条件”与”既不充分也不必要条件“中选出适当的一种填空.充分不必要条件必要不充分条件必要不充分条件充分不必要条件充要条件充要条件既不充分又不必要条件练习2.已知A是B的必要而不充分条件,C是B的充要
条件,D是C的充分而不必要条件,那么D是A的
条件。例4.已知p,q都是r的必要条件,s是r的充分条件,
q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?练习3.已知p是q的必要而不充分条件,
那么非q是非p的_______________条件.充分不必要变式.非A是非B的充分不必要条件,非C是非B的
充要条件, 则A是C的 条件
必要不充分例5. 已知命题p: ,
命题q: ,
若p是q的必要不充分条件,求实数m的取值范围。一.定义:课堂小结二.判别步骤:① 认清条件和结论。② 考察p q和q p的真假。(2)从定义出发:
首先分清条件和结论,然后运用定义来判断.三.判别的常用方法:(3)从集合的角度出发:
由两个集合之间的包含关系来判断 (1)从命题的角度出发:
原命题“若p则q”或逆否命题(若非q则非p)为真,
就说明p是q的充分条件.1.学案:课后检测
2.预习《充分条件和必要条件(二)》课后作业谢谢!
