数学苏教版选修1-1课件: 2.2.1 椭圆的标准方程 课件(20张)
文档属性
| 名称 | 数学苏教版选修1-1课件: 2.2.1 椭圆的标准方程 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 623.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-03 00:00:00 | ||
图片预览





文档简介
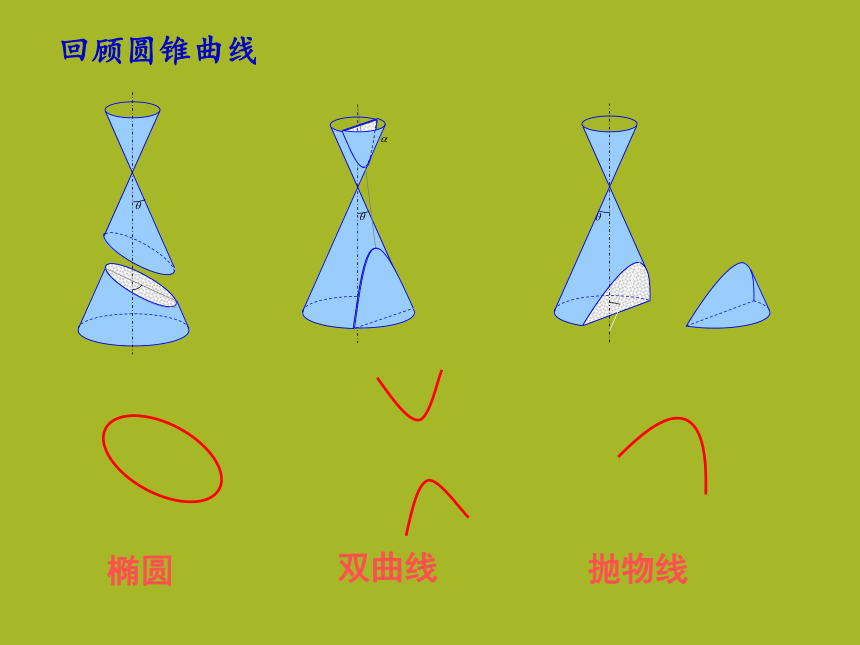
课件20张PPT。2.2.1 椭圆的标准方程(一)椭圆双曲线抛物线回顾圆锥曲线平面内与定点距离等于定长的点的轨迹是圆思考:平面内到两定点距离之和为常数的点的轨迹是什么?
定点是圆心,定长是半径 平面内与两个定点F1、F2的距离和等于常数(2a>|F1F2|)的点的轨迹叫做椭圆.
常数用2a来表示,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.焦距用2c来表示。2a>2c>0
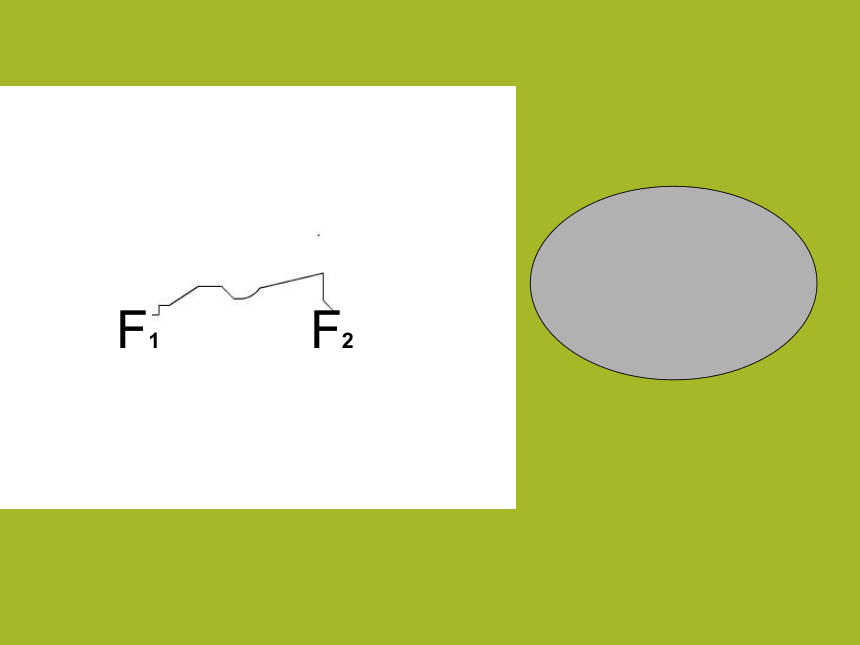
1、椭圆的定义:F1F2 汽车贮油罐的横截面的外轮廓线的形状像椭圆.探究
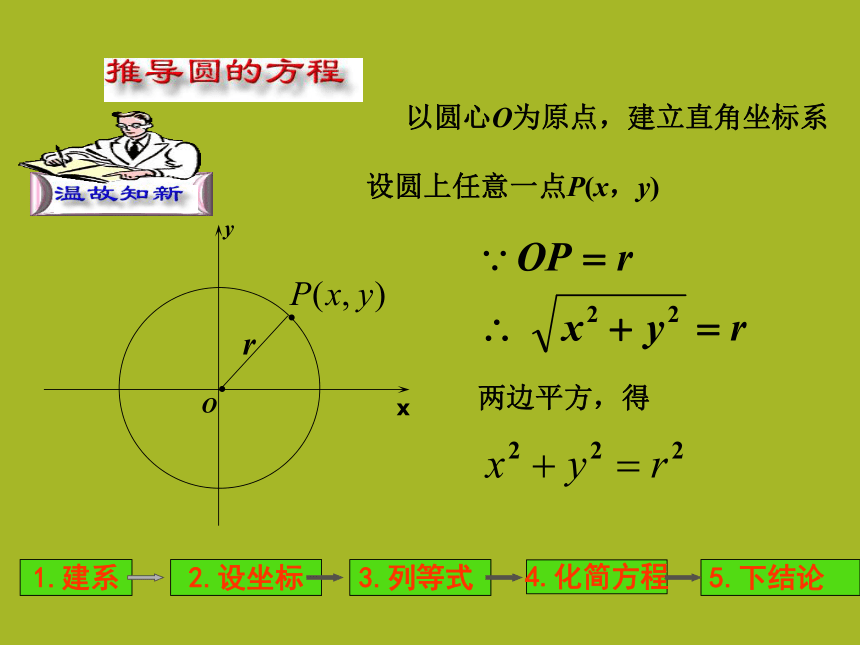
椭圆?Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式4.化简方程5.下结论OxyF1F2M如图所示:F1、F2为两定点,且
|F1F2|=2c,求平面内到两定点
F1、F2距离之和为定值2a(2a>2c)
的动点M的轨迹方程。解:以F1F2所在直线为x轴,线段F1F2的垂直平分线为y轴
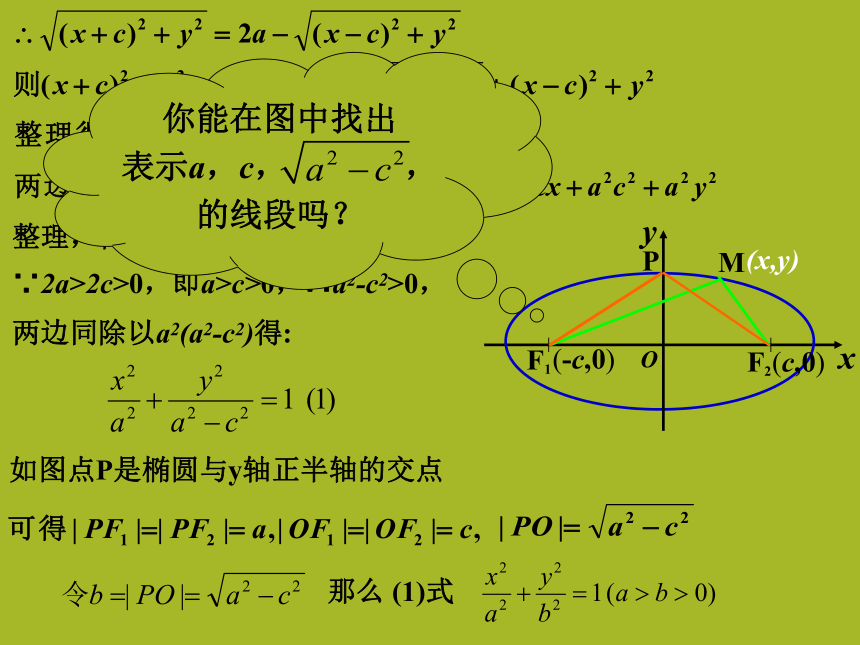
建立直角坐标系,(-c,0)(c,0)(x,y)设M(x,y)为所求轨迹上的任意一点, |MF1|+ |MF2|=2a如何化简?则焦点F1、F2的坐标分别为(-c,0)、(c,0)。问题: 求曲线方程的基本步骤?OxyF1F2M(-c,0)(c,0)(x,y)整理,得 (a2-c2)x2+a2y2=a2(a2-c2)∵2a>2c>0,即a>c>0,∴a2-c2>0,两边同除以a2(a2-c2)得:P那么 (1)式如图点P是椭圆与y轴正半轴的交点你能在图中找出
表示a,c, ,
的线段吗?OOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的再认识:(1)等式左边是两个分式的平方和,等式右边是1(3)椭圆的标准方程中都有a2=b2+c2。并且a总是最大的(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点就在
哪一个轴上。543(3,0)、(-3,0)63.定义的简单应用716(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________; 若CD为过上焦点F2的弦,则 F1CD的周长为________21(0,-1)、(0,1)2XY练习:例3、求适合下列条件的椭圆的标准方程(1)a=4,b=3,焦点在x轴上;
(2)b=5,c=12,焦点在y轴上;
(3)a=10,c=6
(4)焦点为F1(-3,0),F2(3,0),且经过点(0,2);
(5)焦点为F1(0,-1), F2 (0,1),且b=1;
(6)焦点为F1(-2,0),F2(2,0),且经过点
(7)经过点1.方程建立的过程:建立直角坐标系设坐标列等式化简方程下结论小 结2.根据已知条件求椭圆的标准方程:(1)确定焦点所在的位置,选择标准方程的形式;
(2)求解a,b的值,写出椭圆的标准方程.定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系{P|PF1+PF2=2a,2a>F1F2}3.两种标准方程的比较.谢谢各位老师给予指导!
定点是圆心,定长是半径 平面内与两个定点F1、F2的距离和等于常数(2a>|F1F2|)的点的轨迹叫做椭圆.
常数用2a来表示,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.焦距用2c来表示。2a>2c>0
1、椭圆的定义:F1F2 汽车贮油罐的横截面的外轮廓线的形状像椭圆.探究
椭圆?Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式4.化简方程5.下结论OxyF1F2M如图所示:F1、F2为两定点,且
|F1F2|=2c,求平面内到两定点
F1、F2距离之和为定值2a(2a>2c)
的动点M的轨迹方程。解:以F1F2所在直线为x轴,线段F1F2的垂直平分线为y轴
建立直角坐标系,(-c,0)(c,0)(x,y)设M(x,y)为所求轨迹上的任意一点, |MF1|+ |MF2|=2a如何化简?则焦点F1、F2的坐标分别为(-c,0)、(c,0)。问题: 求曲线方程的基本步骤?OxyF1F2M(-c,0)(c,0)(x,y)整理,得 (a2-c2)x2+a2y2=a2(a2-c2)∵2a>2c>0,即a>c>0,∴a2-c2>0,两边同除以a2(a2-c2)得:P那么 (1)式如图点P是椭圆与y轴正半轴的交点你能在图中找出
表示a,c, ,
的线段吗?OOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的再认识:(1)等式左边是两个分式的平方和,等式右边是1(3)椭圆的标准方程中都有a2=b2+c2。并且a总是最大的(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点就在
哪一个轴上。543(3,0)、(-3,0)63.定义的简单应用716(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________; 若CD为过上焦点F2的弦,则 F1CD的周长为________21(0,-1)、(0,1)2XY练习:例3、求适合下列条件的椭圆的标准方程(1)a=4,b=3,焦点在x轴上;
(2)b=5,c=12,焦点在y轴上;
(3)a=10,c=6
(4)焦点为F1(-3,0),F2(3,0),且经过点(0,2);
(5)焦点为F1(0,-1), F2 (0,1),且b=1;
(6)焦点为F1(-2,0),F2(2,0),且经过点
(7)经过点1.方程建立的过程:建立直角坐标系设坐标列等式化简方程下结论小 结2.根据已知条件求椭圆的标准方程:(1)确定焦点所在的位置,选择标准方程的形式;
(2)求解a,b的值,写出椭圆的标准方程.定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系{P|PF1+PF2=2a,2a>F1F2}3.两种标准方程的比较.谢谢各位老师给予指导!
