17.1 勾股定理(1)课件
图片预览







文档简介
人教版数学八年级下册
17.1勾股定理(1)
1.角
2.边
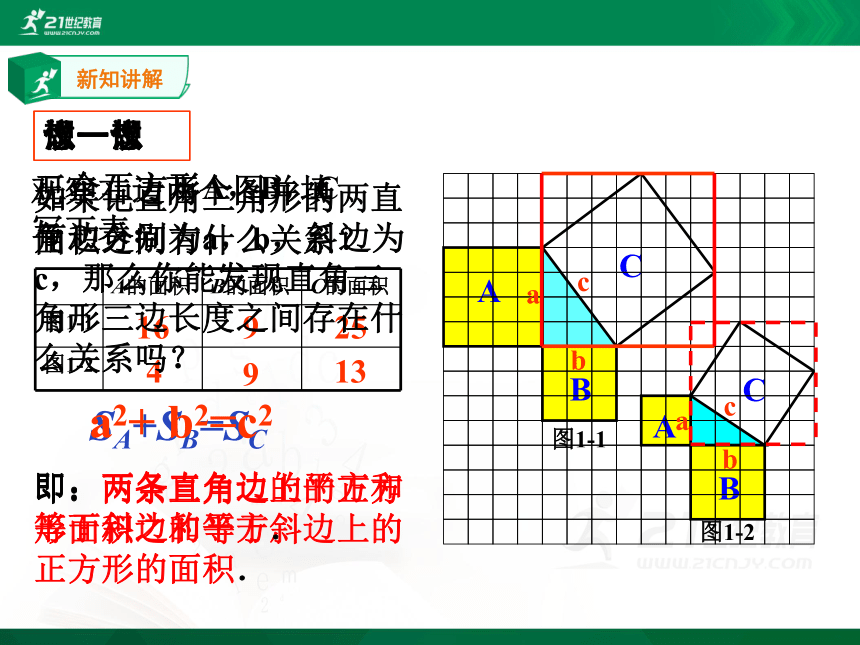
观察右边两个图并填写下表:
16
9
25
4
9
13
做一做
议一议
三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
想一想
如果记直角三角形的两直角边分别为a,b,斜边为c,那么你能发现直角三角形三边长度之间存在什么关系吗?
a2+ b2=c2
即:两条直角边的平方和等于斜边的平方.
A的面积 B的面积 C的面积
图1-1
图1-2
我们的猜想是否真的正确呢?这就需要我们从理论上进行逻辑推导与证明.到目前为止,对这个命题的证明方法已有几百种之多.这里我们一起来了解几种,首先来看看我国数学家赵爽是怎样证明这个命题的.
结 论
赵爽弦图的证法
化简得:
c2 =a2+ b2
c
c
c
S大正方形 S小正方形 4S直角三角形
证法一
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。
化简得:a2 +b2 =c2
证法二
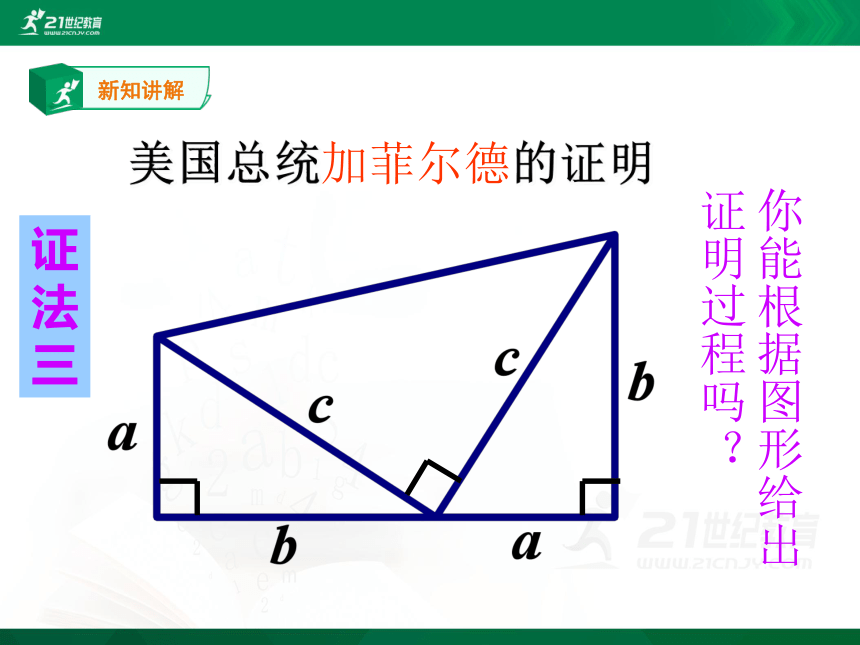
美国总统加菲尔德的证明
证法三
你能根据图形给出证明过程吗?
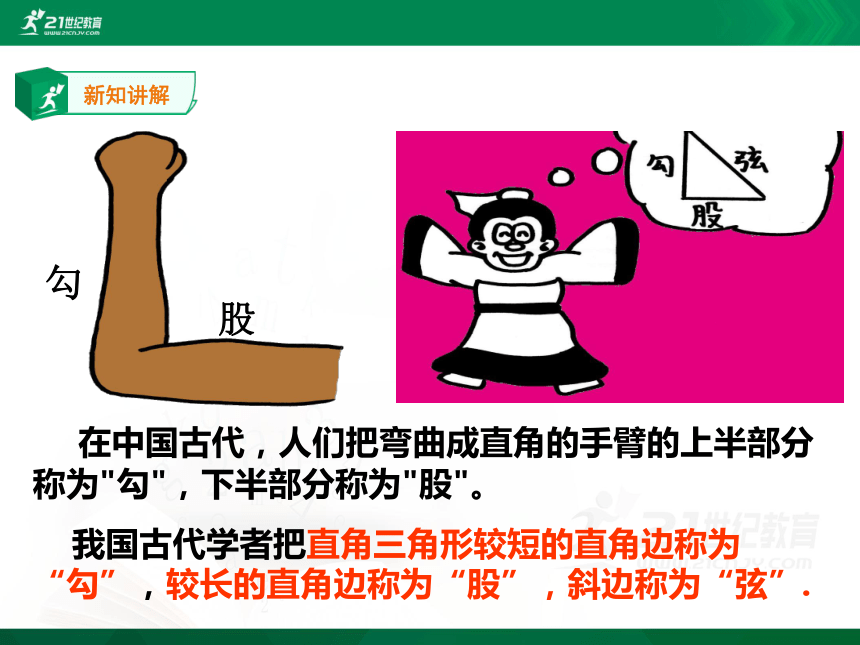
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾 股 定 理
如果直角三角形两直角边分别为a、b,斜边为c,那么
国外又叫毕达哥拉斯定理
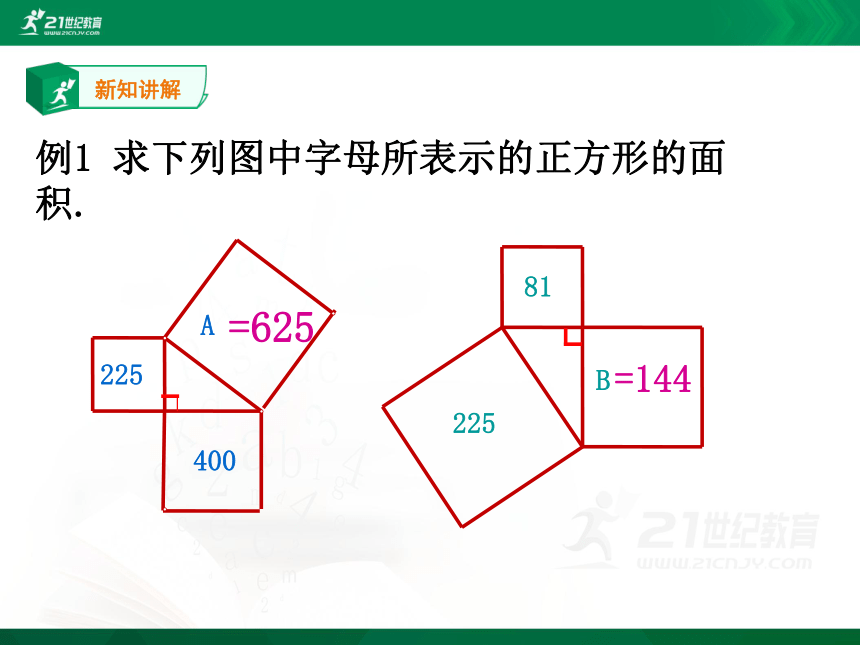
例1 求下列图中字母所表示的正方形的面积.
=625
=144
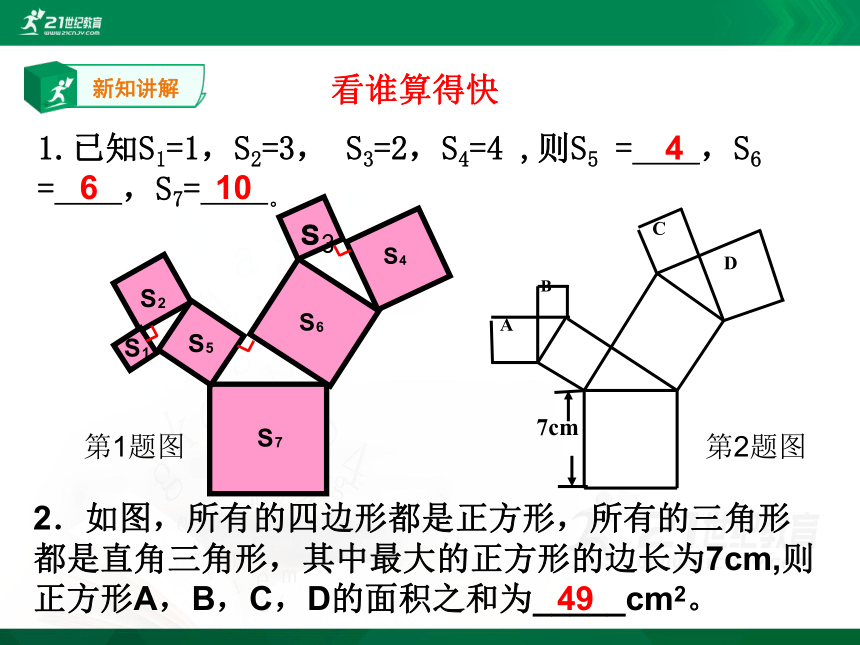
1.已知S1=1,S2=3, S3=2,S4=4 ,则S5 = ,S6 = ,S7= 。
看谁算得快
4
6
10
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为_____cm2。
第1题图
第2题图
49
例2 求出下列直角三角形中未知边的长度.
方法总结:利用勾股定理建立方程.
解:
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
1.在Rt△ABC中, a=5,c=13,则下列计算正确的是( )
B
2.求下列直角三角形中未知边的长度.
⑴已知: a=3, b=4,求c。
⑵已知: c =25,a=7,求b。
3.已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
4.已知: c =10,a=6,
求阴影部分的面积。
5
24
8π
常用的勾股数:
例3 已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________.
(提示:题目指明了哪条边是斜边吗?)
判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2 ( )
2) 直角三角形的两边长分别是3和4,则第三边长是5. ( )
×
×
1.勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
2.了解用面积法证明勾股定理
A
C
B
A
B
C
4 .直角三角形的三边长分别为3,4,x,则x2等于( )
A.5 B.25 C.7 D.25或7
5.已知Rt△ABC中,∠C=90°,若BC=4,AC=2,则AB=______;若AB=4,BC=2,则AC=______.
D
6.已知:∠C=90°,a=6, a:b=3:4,则b= ,c= 。
10
8
7.如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
625
8.图中已知数据表示面积,求表示边的未知数x、y的值.
9.求下列直角三角形中未知边的长:
x=15
x=12
x=13
目前世界上许多科学家正在试图寻找其它星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言,音乐,各种图形等.我国数学家华罗庚建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的.
美丽的勾股树
作业
收集有关勾股定理的其它证明方法,下节课展示、交流.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.1勾股定理(1)
1.角
2.边
观察右边两个图并填写下表:
16
9
25
4
9
13
做一做
议一议
三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
想一想
如果记直角三角形的两直角边分别为a,b,斜边为c,那么你能发现直角三角形三边长度之间存在什么关系吗?
a2+ b2=c2
即:两条直角边的平方和等于斜边的平方.
A的面积 B的面积 C的面积
图1-1
图1-2
我们的猜想是否真的正确呢?这就需要我们从理论上进行逻辑推导与证明.到目前为止,对这个命题的证明方法已有几百种之多.这里我们一起来了解几种,首先来看看我国数学家赵爽是怎样证明这个命题的.
结 论
赵爽弦图的证法
化简得:
c2 =a2+ b2
c
c
c
S大正方形 S小正方形 4S直角三角形
证法一
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。
化简得:a2 +b2 =c2
证法二
美国总统加菲尔德的证明
证法三
你能根据图形给出证明过程吗?
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾 股 定 理
如果直角三角形两直角边分别为a、b,斜边为c,那么
国外又叫毕达哥拉斯定理
例1 求下列图中字母所表示的正方形的面积.
=625
=144
1.已知S1=1,S2=3, S3=2,S4=4 ,则S5 = ,S6 = ,S7= 。
看谁算得快
4
6
10
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为_____cm2。
第1题图
第2题图
49
例2 求出下列直角三角形中未知边的长度.
方法总结:利用勾股定理建立方程.
解:
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
1.在Rt△ABC中, a=5,c=13,则下列计算正确的是( )
B
2.求下列直角三角形中未知边的长度.
⑴已知: a=3, b=4,求c。
⑵已知: c =25,a=7,求b。
3.已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
4.已知: c =10,a=6,
求阴影部分的面积。
5
24
8π
常用的勾股数:
例3 已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________.
(提示:题目指明了哪条边是斜边吗?)
判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2 ( )
2) 直角三角形的两边长分别是3和4,则第三边长是5. ( )
×
×
1.勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
2.了解用面积法证明勾股定理
A
C
B
A
B
C
4 .直角三角形的三边长分别为3,4,x,则x2等于( )
A.5 B.25 C.7 D.25或7
5.已知Rt△ABC中,∠C=90°,若BC=4,AC=2,则AB=______;若AB=4,BC=2,则AC=______.
D
6.已知:∠C=90°,a=6, a:b=3:4,则b= ,c= 。
10
8
7.如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
625
8.图中已知数据表示面积,求表示边的未知数x、y的值.
9.求下列直角三角形中未知边的长:
x=15
x=12
x=13
目前世界上许多科学家正在试图寻找其它星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言,音乐,各种图形等.我国数学家华罗庚建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的.
美丽的勾股树
作业
收集有关勾股定理的其它证明方法,下节课展示、交流.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
