北师大版高中数学必修三:3.2 古典概型 课件
文档属性
| 名称 | 北师大版高中数学必修三:3.2 古典概型 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 680.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-04 08:57:00 | ||
图片预览





文档简介
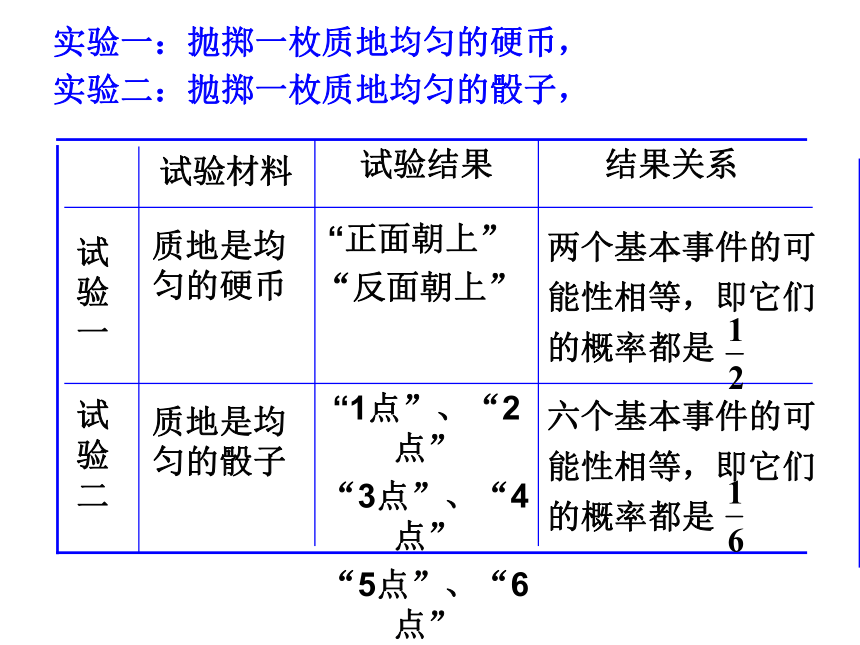
课件27张PPT。3.2 古典概型 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?密码是……想一想“1点”、“2点”
“3点”、“4点”
“5点”、“6点” “正面朝上”
“反面朝上” 试验结果六个基本事件的可能性相等,即它们的概率都是 质地是均匀的骰子试验二两个基本事件的可能性相等,即它们的概率都是 质地是均匀的硬币试验一结果关系试验材料实验一:抛掷一枚质地均匀的硬币,实验二:抛掷一枚质地均匀的骰子,(2)任何事件(除不可能事件)都可以
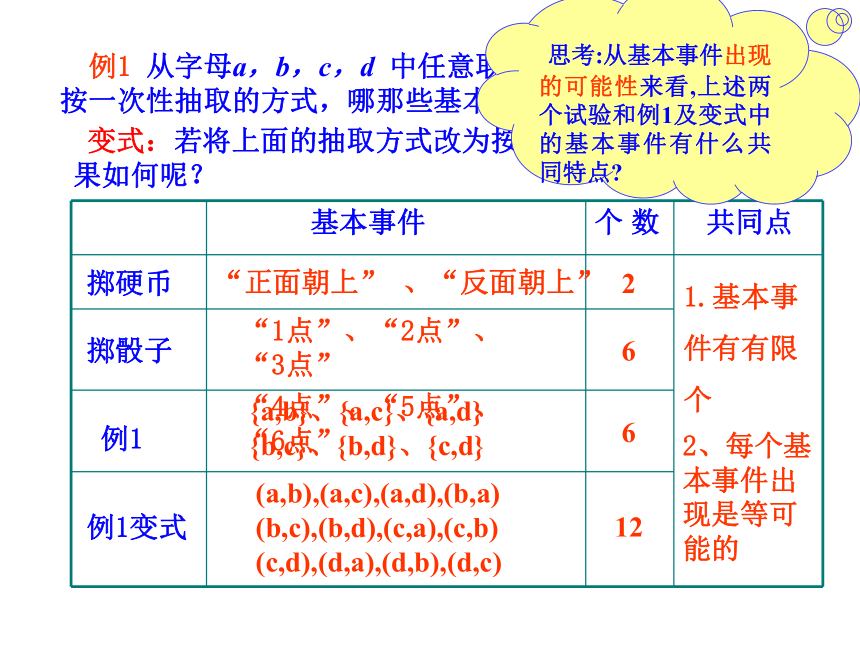
表示成基本事件的和.基本事件有如下特点:(1)任何两个基本事件是互斥的;1.我们把上述试验中的这类随机事件称为基本事件,它是试验的每一个可能结果。 例1 从字母a,b,c,d 中任意取出两个不同字母的实验中,按一次性抽取的方式,哪那些基本事件? 变式:若将上面的抽取方式改为按先后顺序依次抽取,结果如何呢?“正面朝上” 、“反面朝上”2“1点”、“2点”、“3点”
“4点”、“5点”、“6点”66(a,b),(a,c),(a,d),(b,a)
(b,c),(b,d),(c,a),(c,b)
(c,d),(d,a),(d,b),(d,c)12 1.基本事
件有有限
个
{a,b}、{a,c}、{a,d}
{b,c}、{b,d}、{c,d}例1变式
掷骰子掷硬币 例12、每个基本事件出现是等可能的 思考:从基本事件出现的可能性来看,上述两个试验和例1及变式中的基本事件有什么共同特点?
①试验中所有可能出现的基本事件只有有限个;(有限性)
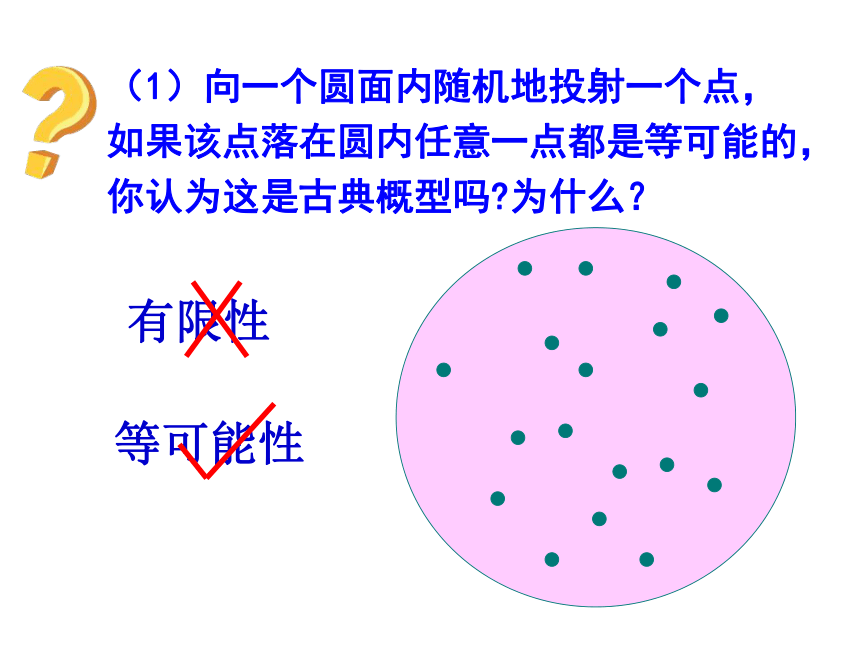
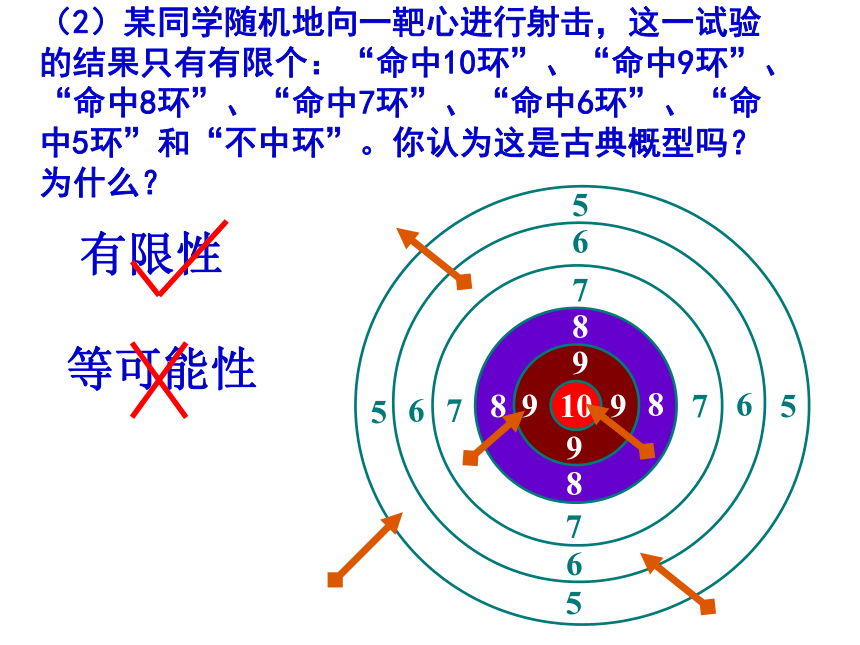
②每个基本事件出现的可能性相等。(等可能性)2、古典概率模型,简称古典概型。有限性等可能性(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?(2)某同学随机地向一靶心进行射击,这一试验的结果只有有限个:“命中10环”、“命中9环”、“命中8环”、“命中7环”、“命中6环”、“命中5环”和“不中环”。你认为这是古典概型吗?为什么?有限性等可能性
①在抛掷一枚质地均匀的硬币试验中,“正面朝上” 的概率是多少?
②在抛掷一枚质地均匀的骰子试验中,“出现点数为1”的概率是多少?
③在抛掷一枚质地均匀的骰子试验中,“出现奇数点”的概率是多少?
思考:在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
试验一:
P(“正面朝上”)=P(“反面朝上”)
由概率的加法公式,得:
P(“正面朝上”)+P(“反面朝上”)=P(“必然事件”)=1
P(“正面朝上”)=P(“反面朝上”)=1/2
所以,试验二:
P(“1点”)= P(“2点”)= P(“3点”)
= P(“4点”)= P(“5点”)= P(“6点”)
由概率的加法公式,得:
P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”)
+P(“5点”)+P(“6点”)=P(“必然事件”)=1
所以:P(“1点”)= P(“2点”)= P(“3点”)= P(“4点”)
= P(“5点”)= P(“6点”)=1/6
3、古典概型概率计算公式: 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?基本事件总数有1000000个。记事件A表示“试一次密码就能取到钱”,它包含的基本事件个数为1, 解:
这是一个古典概型,则,由古典概型的概率计算公式得:问题解决 解:这是一个古典概型,则,由古典概型的概率计算公式得:例2、单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考查的内容,他可以选择唯一正确的答案.假设考生不会做,他随机地选择一个答案,问他答对的概率是多少?基本事件共有4个:{选择A};{选择B};{选择C};{选择D}设事件A表示“答对”,它包含的基本事件个数为1 解:排除A选项之后,从B、C、D三个选项中选择一个正确答案同样也是一个古典概型,基本事件共有3个:则,由古典概型的概率计算公式得:变式:如果考生不会做,但可以根据常识从A,B,C,D四个选项中排除一个选项(比如排除A),问此时这位考生答对的概率是多少?{选择B};{选择C};{选择D}设事件A表示“答对”,它包含的基本事件个数为1探究2:在标准化的考试中既有单选题又有不定项选择题,不定项选择题是从A、B、C、D四个选项中选出所有正确的答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?基本事件有:{A};{B};{C};{D}{A、B};{B、C};{A、C};{A、D};{B、D};{C、D};{A、B、C};{B、 C 、D };{A、B 、D};{A、C、 D};{A 、B 、 C、 D};P(“答对”)=例3 同时掷两个骰子,计算:
(1)一共有多少种不同的等可能结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
(4)若以两颗骰子的点数和打赌,你认为压几
点最有利?.例2 同时掷两个骰子,计算:
(1)一共有多少种不同的等可能结果?.例2 同时掷两个骰子,计算:
(2)其中向上的点数之和是5的结果有多少种?解:.由上表可知,向上的点数之和是5的结果有4种.(1,4)(3,2)(2,3)(4,1)例2 同时掷两个骰子,计算:
(3)向上的点数之和是5的概率是多少?解:. 设事件A表示“向上点数之和为5”,由(2)可知,事件A包含的基本事件个数为4个.于是由古典概型的概率计算公式可得例2 同时掷两个骰子,计算:
(4)若以两颗骰子的点数和打赌,你认为压几点最有利? (1,6)(2,5)(3,4)(4,3)(5,2)(6,1).思考与探究为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? 如果不标上记号,类似于(1,2)和(2,1)的结果将没有区别。这时,所有可能的结果将是: (3,2)(4,1)古典概型解题步骤:(1)阅读题目,搜集信息;(2)判断试验是否为古典概型;(3)求出基本事件总数n和事件A所包含的结果数m;练一练(1) 甲、乙、丙在“五·一”3天节日中值班,每人值班1天,甲排在乙前面值班的概率是多少?基本事件有:
{甲,乙,丙}, {甲,丙,乙}, {乙,甲,丙},
{乙,丙,甲}, {丙,甲,乙}, {丙,乙,甲}.因此,甲排在乙前面的概率为:基本事件有:
{甲,乙,丙}, {甲,丙,乙}, {乙,甲,丙},
{乙,丙,甲}, {丙,甲,乙}, {丙,乙,甲}.解:设A表示“甲排在乙前面”(2) 某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽取2听,检测出不合格产品的概率有多大?练一练 (2).古典概型的定义和特点:(3).古典概型计算任何事件的概率计算公式:(1).基本事件的两个特点:P(A)=归纳反思小结
“3点”、“4点”
“5点”、“6点” “正面朝上”
“反面朝上” 试验结果六个基本事件的可能性相等,即它们的概率都是 质地是均匀的骰子试验二两个基本事件的可能性相等,即它们的概率都是 质地是均匀的硬币试验一结果关系试验材料实验一:抛掷一枚质地均匀的硬币,实验二:抛掷一枚质地均匀的骰子,(2)任何事件(除不可能事件)都可以
表示成基本事件的和.基本事件有如下特点:(1)任何两个基本事件是互斥的;1.我们把上述试验中的这类随机事件称为基本事件,它是试验的每一个可能结果。 例1 从字母a,b,c,d 中任意取出两个不同字母的实验中,按一次性抽取的方式,哪那些基本事件? 变式:若将上面的抽取方式改为按先后顺序依次抽取,结果如何呢?“正面朝上” 、“反面朝上”2“1点”、“2点”、“3点”
“4点”、“5点”、“6点”66(a,b),(a,c),(a,d),(b,a)
(b,c),(b,d),(c,a),(c,b)
(c,d),(d,a),(d,b),(d,c)12 1.基本事
件有有限
个
{a,b}、{a,c}、{a,d}
{b,c}、{b,d}、{c,d}例1变式
掷骰子掷硬币 例12、每个基本事件出现是等可能的 思考:从基本事件出现的可能性来看,上述两个试验和例1及变式中的基本事件有什么共同特点?
①试验中所有可能出现的基本事件只有有限个;(有限性)
②每个基本事件出现的可能性相等。(等可能性)2、古典概率模型,简称古典概型。有限性等可能性(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?(2)某同学随机地向一靶心进行射击,这一试验的结果只有有限个:“命中10环”、“命中9环”、“命中8环”、“命中7环”、“命中6环”、“命中5环”和“不中环”。你认为这是古典概型吗?为什么?有限性等可能性
①在抛掷一枚质地均匀的硬币试验中,“正面朝上” 的概率是多少?
②在抛掷一枚质地均匀的骰子试验中,“出现点数为1”的概率是多少?
③在抛掷一枚质地均匀的骰子试验中,“出现奇数点”的概率是多少?
思考:在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
试验一:
P(“正面朝上”)=P(“反面朝上”)
由概率的加法公式,得:
P(“正面朝上”)+P(“反面朝上”)=P(“必然事件”)=1
P(“正面朝上”)=P(“反面朝上”)=1/2
所以,试验二:
P(“1点”)= P(“2点”)= P(“3点”)
= P(“4点”)= P(“5点”)= P(“6点”)
由概率的加法公式,得:
P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”)
+P(“5点”)+P(“6点”)=P(“必然事件”)=1
所以:P(“1点”)= P(“2点”)= P(“3点”)= P(“4点”)
= P(“5点”)= P(“6点”)=1/6
3、古典概型概率计算公式: 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?基本事件总数有1000000个。记事件A表示“试一次密码就能取到钱”,它包含的基本事件个数为1, 解:
这是一个古典概型,则,由古典概型的概率计算公式得:问题解决 解:这是一个古典概型,则,由古典概型的概率计算公式得:例2、单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考查的内容,他可以选择唯一正确的答案.假设考生不会做,他随机地选择一个答案,问他答对的概率是多少?基本事件共有4个:{选择A};{选择B};{选择C};{选择D}设事件A表示“答对”,它包含的基本事件个数为1 解:排除A选项之后,从B、C、D三个选项中选择一个正确答案同样也是一个古典概型,基本事件共有3个:则,由古典概型的概率计算公式得:变式:如果考生不会做,但可以根据常识从A,B,C,D四个选项中排除一个选项(比如排除A),问此时这位考生答对的概率是多少?{选择B};{选择C};{选择D}设事件A表示“答对”,它包含的基本事件个数为1探究2:在标准化的考试中既有单选题又有不定项选择题,不定项选择题是从A、B、C、D四个选项中选出所有正确的答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?基本事件有:{A};{B};{C};{D}{A、B};{B、C};{A、C};{A、D};{B、D};{C、D};{A、B、C};{B、 C 、D };{A、B 、D};{A、C、 D};{A 、B 、 C、 D};P(“答对”)=例3 同时掷两个骰子,计算:
(1)一共有多少种不同的等可能结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
(4)若以两颗骰子的点数和打赌,你认为压几
点最有利?.例2 同时掷两个骰子,计算:
(1)一共有多少种不同的等可能结果?.例2 同时掷两个骰子,计算:
(2)其中向上的点数之和是5的结果有多少种?解:.由上表可知,向上的点数之和是5的结果有4种.(1,4)(3,2)(2,3)(4,1)例2 同时掷两个骰子,计算:
(3)向上的点数之和是5的概率是多少?解:. 设事件A表示“向上点数之和为5”,由(2)可知,事件A包含的基本事件个数为4个.于是由古典概型的概率计算公式可得例2 同时掷两个骰子,计算:
(4)若以两颗骰子的点数和打赌,你认为压几点最有利? (1,6)(2,5)(3,4)(4,3)(5,2)(6,1).思考与探究为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? 如果不标上记号,类似于(1,2)和(2,1)的结果将没有区别。这时,所有可能的结果将是: (3,2)(4,1)古典概型解题步骤:(1)阅读题目,搜集信息;(2)判断试验是否为古典概型;(3)求出基本事件总数n和事件A所包含的结果数m;练一练(1) 甲、乙、丙在“五·一”3天节日中值班,每人值班1天,甲排在乙前面值班的概率是多少?基本事件有:
{甲,乙,丙}, {甲,丙,乙}, {乙,甲,丙},
{乙,丙,甲}, {丙,甲,乙}, {丙,乙,甲}.因此,甲排在乙前面的概率为:基本事件有:
{甲,乙,丙}, {甲,丙,乙}, {乙,甲,丙},
{乙,丙,甲}, {丙,甲,乙}, {丙,乙,甲}.解:设A表示“甲排在乙前面”(2) 某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽取2听,检测出不合格产品的概率有多大?练一练 (2).古典概型的定义和特点:(3).古典概型计算任何事件的概率计算公式:(1).基本事件的两个特点:P(A)=归纳反思小结
