第五课时 连加教案
图片预览



文档简介
第五课时 连加
教学内容
教材75~76页 能够用不同方法计算三个数相加,会进行连加计算
教学提示
学生在日常生活中对三个数相加已经积累了一些感性经验。教学时充分利用情境图,和学生的生活经验,让学生动脑思考,动嘴描述,体会连加计算的思维方法,理解知识的发展过程。
教学目标
知识与技能:结合具体情境,经历尝试计算三个数相加、认识连加算式的过程。
过程与方法:能够用不同方法计算三个数相加,会进行连加计算。
情感态度与价值观:了解可以用不同方法解决问题,获得数学学习的成功体验。
重点、难点
重点:能够用不同的方法计算三个数相加,了解连加的意义。
难点:会进行连加计算。
教学准备
教具准备:主题图、课件、数字卡片。
学具准备:数字卡片。
教学过程
一、新课导入。
师:快看!动物王国要举行长跑比赛(课件出示教材75页情景图)。你们瞧,长颈鹿、驯鹿、梅花鹿都来参加选拔。你们喜欢这些可爱的动物们吗?(生:喜欢)今天我们跟着它们一起学习用连加解决问题。(板书:连加)
设计意图:紧密结合生活实际,从孩子们最感兴趣的活动引入,再配以生动的画面,能够促使孩子们趣味盎然地走进课堂,参与学习。
探求新知---连加。
(一)“一共有多少只鹿”。
师:观察情景图,你知道了哪些数学信息?
生1:图中有3只长颈鹿。
生2:图中有5只驯鹿。
生3:图中有7只梅花鹿。
(教师适时板书对应的数字)
师:你们观察得真细致!发现了这么多信息,鹿王想知道参加选拔的一共有多少只鹿?你能帮助它算出来吗?我相信你们一定会有好办法的。试一试!
(给学生充分时间独立思考并书写算式,然后组内交流各自的算法,最后全班汇报)
师:哪名同学愿意把自己的算法和结果分享给大家?
生1:我先算出3只长颈鹿和5只驯鹿的数量和,即3+5=8;再和7只梅花鹿的数量合在一起,即8+7=15;所以一共有15只鹿。(学生边说,教师边板书算式)
生2:我是这样想的,我先求出3只长颈鹿和7只梅花鹿的数量和,即3+7=10;再和5只驯鹿的数量合在一起,即10+5=15;所以一共有15只鹿。(学生边说,教师边板书算式)
......
师:通过同学们详细的讲解,虽然同学们选择的算法不同,但是我们算出来鹿的总数量不变,都是15只。你们解答得都非常棒!下面我们先仔细观察生1(手指板书上两个算式:3+5=8,8+7=15),你发现了什么?
生1:这两个算式都是加法算式。
生2:我发现第二个算式的第一个加数8,也是第一个加法算式的和。
师:观察真认真,你真了不起!我们可以把第二个加法算式的第一个加数8换成一个第一个加法算式,你能根据我的提示改写算式吗?
生:3+5+7=15,这样写算式,行吗?
师:当然可以了,并且改写完全正确!三个数相加可以写成一个算式3+5+7,这样的算式叫做连加。计算没有小括号的连加运算顺序是从左往右依次计算,即:先算3+5=8,再算8+7=15.(教师边说边板书)你们能用同样的方法把生2(用手指板书:3+7=10,10+5=15)这一组加法算式吗?并尝试着说一说运算顺序,也就是先算哪个算式的和,再算哪个算式的和。
生1:3+7+5=15.
生2:3+7+5=15,先算3+7=10,再算10+5=15.
设计意图:相信孩子们能学会,放手让他们去学,使得他们在独立思考与合作交流中,感悟获得新知,体验探究的乐趣,品味合作的快乐。
观察金鱼图,鼓励学生发现图中的数学信息,提出问题和列出连加算式进行自主计算的要求。让学生自主尝试。
(课件出示教材75页试一试)
师:你们能运用刚刚学习的新知识解决“金鱼”情景图中的问题吗?观察金鱼情景图,你知道了哪些数学信息?
生:三个鱼缸的金鱼条数分别是8条、6条和5条。
师:请你试着列出一个连加算式,并算一算一共有多少条鱼?
(给学生独立思考并列出相应算式时间,然后组内交流各自的算法,最后全班汇报)
(交流列出的算式和计算的结果时,给学生充分交流不同算式和算法的机会。对学生个性的算法进行鼓励性评价)
设计意图:请同学们利用所学知识再次解决疑问,一方面让他们感觉到老师对他们的无比信任,他们自然会竭尽全力解答疑惑;另一方面再次运用连加解决问题,从而达到巩固新知的目的。
三、巩固知新。
1.练一练。第1题。
(1)出示示意图,让学生观察,说说从示意图中了解到哪些数学信息?
(2)鼓励学生根据图中的数学信息提出问题并解答。
(3)同学之间交流各自的算法,并指名读出自己的答案。
2. 练一练,第2题。
让学生独立完成。交流时,说一说各自的算法。
设计意图:通过引导学生认真观察画面,实际演示算法等方式,引导学生大胆讨论,全班交流,从中发现问题,解决问题,培养了学生认真观察、善于思考的习惯。
四、达标反馈。
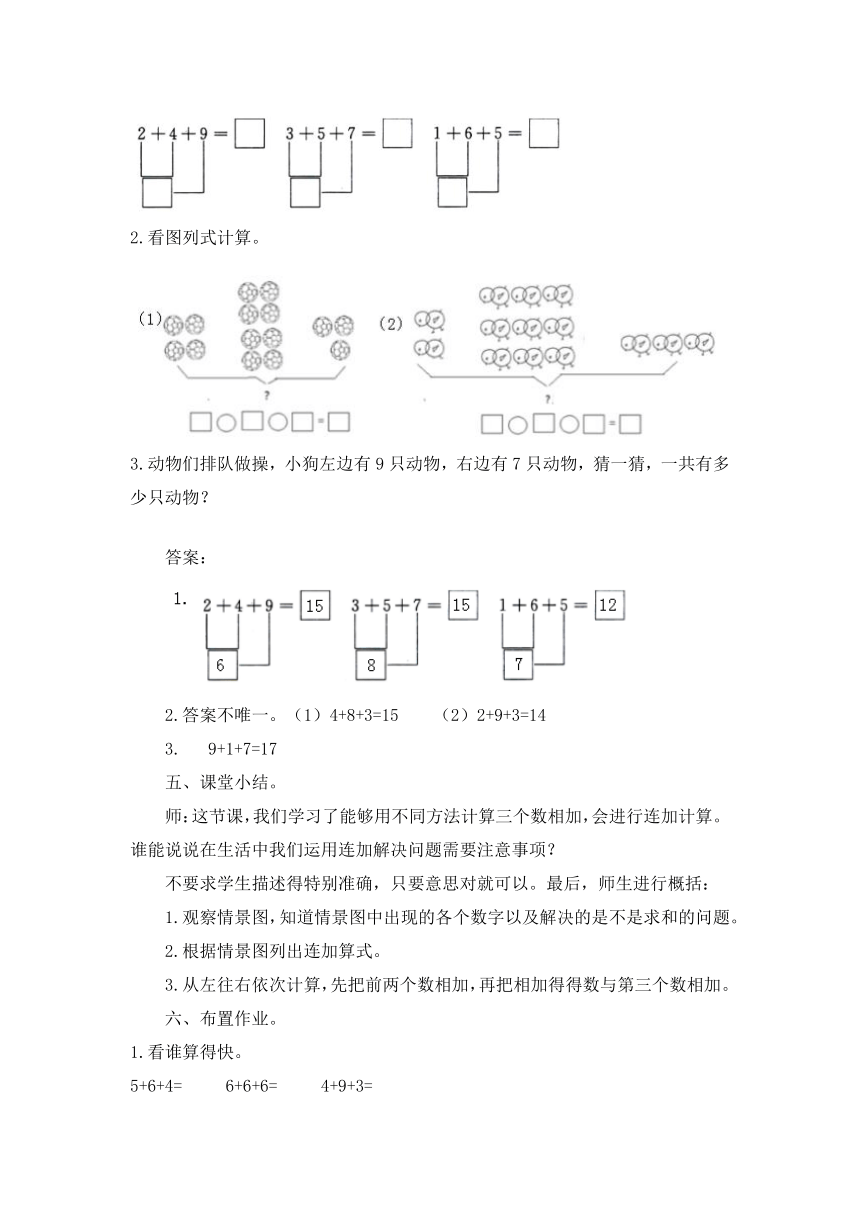
1.算一算。
/
2.看图列式计算。
/
3.动物们排队做操,小狗左边有9只动物,右边有7只动物,猜一猜,一共有多少只动物?
答案:
/
答案不唯一。(1)4+8+3=15 (2)2+9+3=14
9+1+7=17
五、课堂小结。
师:这节课,我们学习了能够用不同方法计算三个数相加,会进行连加计算。谁能说说在生活中我们运用连加解决问题需要注意事项?
不要求学生描述得特别准确,只要意思对就可以。最后,师生进行概括:
1.观察情景图,知道情景图中出现的各个数字以及解决的是不是求和的问题。
2.根据情景图列出连加算式。
3.从左往右依次计算,先把前两个数相加,再把相加得得数与第三个数相加。
六、布置作业。
1.看谁算得快。
5+6+4= 6+6+6= 4+9+3=
7+8+2= 9+4+5= 2+8+5=
9+3+6= 8+4+3= 7+6+5=
看图列式计算。
/
3.解决问题。
(1)/
/
(2)/
/
答案:
1. 15 12 16 17 18 15 18 15 18
2. 4+3+6=13
3.(1)4+4+3=11 (2)8+3+2=13
板书设计
连加
3+5=8 3+7=10
8+7=15 10+5=15
3+5+7=15 3+7+5=15
计算没有小括号的连加
运算顺序是从左往右依次
计算,即:先算3+5=8,
再算8+7=15.
教学反思
本节课一开始首先观察情景图,通过列式子,得出连加的含义,有两个加号,三个数相加的式子,我们就叫连加。最后讲到连加的式子是怎样计算的,先把第一个数和第二个数相加,再把得数与第三个数相加,从而说出连加式子的计算方法,从左到右的左右顺序计算。最后通过让学生上黑板练习,巩固所学连加的计算方法。在小结过程中,先让学生自己说说,最后加以引导,学习了三个数连加,先把前面两个数相加,把得数再与第三个数相加。最后交流、反思等活动中逐步让学生体会数学知识的产生形成和发展过程,学生在观察中理解,在操作中感知,不仅拓宽了思路,获取了新知识,而且沟通了知识的内涵,领悟了学习方法,转变学习方式,激活学习热情,学生全员参加数学活动,培养了学生的学习能力。进一步感知所学数学知识在生活中的应用价值。
教学资料包
一、教学精彩片段。
(一)(出示数字卡片)
师:你能快速并且准确的算式两个加数相加得和吗?(学生抢答)如果三个数连加,你还会计算吗?你能利用接下来学习的新知识解决这个问题吗?(出示数字卡片:4+5+5=)(板书:连加)
数字卡片:9+5= 9+3= 8+5= 7+6= 9+4=
8+4= 6+9= 2+9= 5+5= 3+7=
(二)“送信”游戏--(参考教材第76页练一练第3题)。
师:同学们看,这是什么?(拿出三个信箱)老师这儿有一些信,谁愿意帮老师送一送?
(教师发给举手学生写有算式的卡片,有算式卡片的同学认真看算式并计算出得数)
师:大家都知道自己的信应该送到哪个信箱吗?
生:算式的得数是几,就要把信送到写有数字几的信箱。
师:游戏的要求:在你投信之前,要把你的信举起来让大家看一看,并把信的内容读出来,请同学们判断一下你的信投的是否正确。
(学生投信,其他同学用手势判断正误。如果有误,同学们一起帮助他。)
设计意图:活波有趣的游戏,能够有效的激发孩子们的参与欲望,促使他们积极、主动的参与到复习旧知与巩固新知的过程中。
二、教学资源
用连加描述生活中的事物
1.观察情景图,知道情景图中出现的各个数字以及解决的是不是求和的问题。
2.根据情景图列出连加算式。
3.从左往右依次计算,先把前两个数相加,再把相加得得数与第三个数相加。
?三、资料链接。
(一) 从一加到一百
高斯有许多有趣的故事,故事的第一手资料常来自高斯本人,因为他在晚年时总喜欢谈他小时候的事,我们也许会怀疑故事的真实性,但许多人都证实了他所谈的故事。
高斯的父亲作泥瓦厂的工头,每星期六他总是要发薪水给工人。在高斯三岁夏天时,有一次当父亲正要发薪水的时候,小高斯站了起来说:“爸爸,你弄错了。”然后他说了另外一个数目。原来三岁的小高斯趴在地板上,一直暗地里跟着他爸爸计算该给谁多少工钱。重算的结果证明小高斯是对的,这把站在那里的大人都吓得目瞪口呆。 高斯常常带笑说,他在学讲话之前就已经学会计算了,还常说他问了大人字母如何发音后,就自己学着读起书来。
七岁时高斯进了StCatherine小学。大约在十岁时,老师在算数课上出了一道难题:“把1到100的整数写下来,然后把它们加起来!”每当有考试时他们有如下的习惯:第一个做完的就把石板(当时通行,写字用)面朝下地放在老师的桌子上,第二个做完的就把石板摆在第一张石板上,就这样一个一个摞起来。这个难题当然难不倒学过算数级数的人,但这些孩子才刚开始学算数呢!老师心想他可以休息一下了。但他错了,因为还不到几秒钟,高斯已经把石板放在讲桌上了,同时说道:“答案在这儿!”其他的学生把数字一个个加起来,额头都出了汗水,但高斯却静静坐着,对老师投来的轻蔑的、怀疑的眼光毫不在意。考完后,老师一张张地检查着石板。大部分都做错了,学生就吃了一顿鞭打。
最后,高斯的石板被翻了过来,只见上面只有一个数字:5050(用不着说,这是正确的答案)。老师吃了一惊,高斯就解释他如何找到答案:1+100=101,2+99=101,3+98=101,??,49+52=101,50+51=101,一共有50对和为101的数目,所以答案是50×101=5050。由此可见高斯找到了算术级数的对称性,然后就像求得一般算术级数和的过程一样,把数目一对对地凑在一起。
(二)数论上的“1+2”问题
我国著名数学家陈景润(1933—1996),出生于福州市。在家里排行老三,母亲生了12个孩子,只有6个存活下来。据陈景润回忆说:“在家里我是一个多余的孩子,在学校是一只丑小鸭。但我觉得,一个人不在于外表怎样,而在于志向的高下。”(《工人日报》1989年12月18日)
陈景润从小喜欢数学,抗日战争时期升入初中的时候,从远方的沦陷区搬迁到福州的大学教师也在这个学校兼点课。他特别喜欢两个兼课的数理老师。老师也喜欢他学习善动脑筋。
陈景润在读高中时,教他的数学老师沈元是当时清华大学航空系的系主任(现为北航教授)。沈老师知识渊博,诲人不倦。
有一天,沈老师向全班学生讲了哥德巴赫(C.Goldbach,1690—1764)的故事:“1742年,德国数学家哥德巴赫写了一封信给著名数学家欧拉,提出了一个难题。他发现‘每一个偶数(除2以外)都可以写成两个素数的和’(简称为“1+1”),如4=2+2,6=3+3,8=5+3,10=7+3,??。欧拉想了许久没有解决。有人对一个一个的偶数进行了这样的验算,一直验算到三亿三千万都表明是对的。但是更大更大的数目呢?猜想起来也是对 的,猜想应当证明,要证明却是很难很难的。二百多年过去了,至今尚未解决,”接着沈老师笑着说:“我有一天夜里,梦见我的一个学生证明了这个哥德巴赫猜想。”同学们听罢都笑了,只有陈景润一人没有笑。
陈景润把这个故事深深地记在心里,为解决这个难题,他坚持不懈地计算了20多年,于1966年5月在《科学通报》第17期上证明了“1+2”问题,就是说:任何一个大偶数等于一个素数与另一个不超过两个素数之积的和。这被国外誉为“陈氏定理”。这就是数论上“1+2”问题。
虽然“1+1”问题(哥德巴赫猜想)至今未被解决,但陈景润对它的最终被解决作出了重要贡献。
教学内容
教材75~76页 能够用不同方法计算三个数相加,会进行连加计算
教学提示
学生在日常生活中对三个数相加已经积累了一些感性经验。教学时充分利用情境图,和学生的生活经验,让学生动脑思考,动嘴描述,体会连加计算的思维方法,理解知识的发展过程。
教学目标
知识与技能:结合具体情境,经历尝试计算三个数相加、认识连加算式的过程。
过程与方法:能够用不同方法计算三个数相加,会进行连加计算。
情感态度与价值观:了解可以用不同方法解决问题,获得数学学习的成功体验。
重点、难点
重点:能够用不同的方法计算三个数相加,了解连加的意义。
难点:会进行连加计算。
教学准备
教具准备:主题图、课件、数字卡片。
学具准备:数字卡片。
教学过程
一、新课导入。
师:快看!动物王国要举行长跑比赛(课件出示教材75页情景图)。你们瞧,长颈鹿、驯鹿、梅花鹿都来参加选拔。你们喜欢这些可爱的动物们吗?(生:喜欢)今天我们跟着它们一起学习用连加解决问题。(板书:连加)
设计意图:紧密结合生活实际,从孩子们最感兴趣的活动引入,再配以生动的画面,能够促使孩子们趣味盎然地走进课堂,参与学习。
探求新知---连加。
(一)“一共有多少只鹿”。
师:观察情景图,你知道了哪些数学信息?
生1:图中有3只长颈鹿。
生2:图中有5只驯鹿。
生3:图中有7只梅花鹿。
(教师适时板书对应的数字)
师:你们观察得真细致!发现了这么多信息,鹿王想知道参加选拔的一共有多少只鹿?你能帮助它算出来吗?我相信你们一定会有好办法的。试一试!
(给学生充分时间独立思考并书写算式,然后组内交流各自的算法,最后全班汇报)
师:哪名同学愿意把自己的算法和结果分享给大家?
生1:我先算出3只长颈鹿和5只驯鹿的数量和,即3+5=8;再和7只梅花鹿的数量合在一起,即8+7=15;所以一共有15只鹿。(学生边说,教师边板书算式)
生2:我是这样想的,我先求出3只长颈鹿和7只梅花鹿的数量和,即3+7=10;再和5只驯鹿的数量合在一起,即10+5=15;所以一共有15只鹿。(学生边说,教师边板书算式)
......
师:通过同学们详细的讲解,虽然同学们选择的算法不同,但是我们算出来鹿的总数量不变,都是15只。你们解答得都非常棒!下面我们先仔细观察生1(手指板书上两个算式:3+5=8,8+7=15),你发现了什么?
生1:这两个算式都是加法算式。
生2:我发现第二个算式的第一个加数8,也是第一个加法算式的和。
师:观察真认真,你真了不起!我们可以把第二个加法算式的第一个加数8换成一个第一个加法算式,你能根据我的提示改写算式吗?
生:3+5+7=15,这样写算式,行吗?
师:当然可以了,并且改写完全正确!三个数相加可以写成一个算式3+5+7,这样的算式叫做连加。计算没有小括号的连加运算顺序是从左往右依次计算,即:先算3+5=8,再算8+7=15.(教师边说边板书)你们能用同样的方法把生2(用手指板书:3+7=10,10+5=15)这一组加法算式吗?并尝试着说一说运算顺序,也就是先算哪个算式的和,再算哪个算式的和。
生1:3+7+5=15.
生2:3+7+5=15,先算3+7=10,再算10+5=15.
设计意图:相信孩子们能学会,放手让他们去学,使得他们在独立思考与合作交流中,感悟获得新知,体验探究的乐趣,品味合作的快乐。
观察金鱼图,鼓励学生发现图中的数学信息,提出问题和列出连加算式进行自主计算的要求。让学生自主尝试。
(课件出示教材75页试一试)
师:你们能运用刚刚学习的新知识解决“金鱼”情景图中的问题吗?观察金鱼情景图,你知道了哪些数学信息?
生:三个鱼缸的金鱼条数分别是8条、6条和5条。
师:请你试着列出一个连加算式,并算一算一共有多少条鱼?
(给学生独立思考并列出相应算式时间,然后组内交流各自的算法,最后全班汇报)
(交流列出的算式和计算的结果时,给学生充分交流不同算式和算法的机会。对学生个性的算法进行鼓励性评价)
设计意图:请同学们利用所学知识再次解决疑问,一方面让他们感觉到老师对他们的无比信任,他们自然会竭尽全力解答疑惑;另一方面再次运用连加解决问题,从而达到巩固新知的目的。
三、巩固知新。
1.练一练。第1题。
(1)出示示意图,让学生观察,说说从示意图中了解到哪些数学信息?
(2)鼓励学生根据图中的数学信息提出问题并解答。
(3)同学之间交流各自的算法,并指名读出自己的答案。
2. 练一练,第2题。
让学生独立完成。交流时,说一说各自的算法。
设计意图:通过引导学生认真观察画面,实际演示算法等方式,引导学生大胆讨论,全班交流,从中发现问题,解决问题,培养了学生认真观察、善于思考的习惯。
四、达标反馈。
1.算一算。
/
2.看图列式计算。
/
3.动物们排队做操,小狗左边有9只动物,右边有7只动物,猜一猜,一共有多少只动物?
答案:
/
答案不唯一。(1)4+8+3=15 (2)2+9+3=14
9+1+7=17
五、课堂小结。
师:这节课,我们学习了能够用不同方法计算三个数相加,会进行连加计算。谁能说说在生活中我们运用连加解决问题需要注意事项?
不要求学生描述得特别准确,只要意思对就可以。最后,师生进行概括:
1.观察情景图,知道情景图中出现的各个数字以及解决的是不是求和的问题。
2.根据情景图列出连加算式。
3.从左往右依次计算,先把前两个数相加,再把相加得得数与第三个数相加。
六、布置作业。
1.看谁算得快。
5+6+4= 6+6+6= 4+9+3=
7+8+2= 9+4+5= 2+8+5=
9+3+6= 8+4+3= 7+6+5=
看图列式计算。
/
3.解决问题。
(1)/
/
(2)/
/
答案:
1. 15 12 16 17 18 15 18 15 18
2. 4+3+6=13
3.(1)4+4+3=11 (2)8+3+2=13
板书设计
连加
3+5=8 3+7=10
8+7=15 10+5=15
3+5+7=15 3+7+5=15
计算没有小括号的连加
运算顺序是从左往右依次
计算,即:先算3+5=8,
再算8+7=15.
教学反思
本节课一开始首先观察情景图,通过列式子,得出连加的含义,有两个加号,三个数相加的式子,我们就叫连加。最后讲到连加的式子是怎样计算的,先把第一个数和第二个数相加,再把得数与第三个数相加,从而说出连加式子的计算方法,从左到右的左右顺序计算。最后通过让学生上黑板练习,巩固所学连加的计算方法。在小结过程中,先让学生自己说说,最后加以引导,学习了三个数连加,先把前面两个数相加,把得数再与第三个数相加。最后交流、反思等活动中逐步让学生体会数学知识的产生形成和发展过程,学生在观察中理解,在操作中感知,不仅拓宽了思路,获取了新知识,而且沟通了知识的内涵,领悟了学习方法,转变学习方式,激活学习热情,学生全员参加数学活动,培养了学生的学习能力。进一步感知所学数学知识在生活中的应用价值。
教学资料包
一、教学精彩片段。
(一)(出示数字卡片)
师:你能快速并且准确的算式两个加数相加得和吗?(学生抢答)如果三个数连加,你还会计算吗?你能利用接下来学习的新知识解决这个问题吗?(出示数字卡片:4+5+5=)(板书:连加)
数字卡片:9+5= 9+3= 8+5= 7+6= 9+4=
8+4= 6+9= 2+9= 5+5= 3+7=
(二)“送信”游戏--(参考教材第76页练一练第3题)。
师:同学们看,这是什么?(拿出三个信箱)老师这儿有一些信,谁愿意帮老师送一送?
(教师发给举手学生写有算式的卡片,有算式卡片的同学认真看算式并计算出得数)
师:大家都知道自己的信应该送到哪个信箱吗?
生:算式的得数是几,就要把信送到写有数字几的信箱。
师:游戏的要求:在你投信之前,要把你的信举起来让大家看一看,并把信的内容读出来,请同学们判断一下你的信投的是否正确。
(学生投信,其他同学用手势判断正误。如果有误,同学们一起帮助他。)
设计意图:活波有趣的游戏,能够有效的激发孩子们的参与欲望,促使他们积极、主动的参与到复习旧知与巩固新知的过程中。
二、教学资源
用连加描述生活中的事物
1.观察情景图,知道情景图中出现的各个数字以及解决的是不是求和的问题。
2.根据情景图列出连加算式。
3.从左往右依次计算,先把前两个数相加,再把相加得得数与第三个数相加。
?三、资料链接。
(一) 从一加到一百
高斯有许多有趣的故事,故事的第一手资料常来自高斯本人,因为他在晚年时总喜欢谈他小时候的事,我们也许会怀疑故事的真实性,但许多人都证实了他所谈的故事。
高斯的父亲作泥瓦厂的工头,每星期六他总是要发薪水给工人。在高斯三岁夏天时,有一次当父亲正要发薪水的时候,小高斯站了起来说:“爸爸,你弄错了。”然后他说了另外一个数目。原来三岁的小高斯趴在地板上,一直暗地里跟着他爸爸计算该给谁多少工钱。重算的结果证明小高斯是对的,这把站在那里的大人都吓得目瞪口呆。 高斯常常带笑说,他在学讲话之前就已经学会计算了,还常说他问了大人字母如何发音后,就自己学着读起书来。
七岁时高斯进了StCatherine小学。大约在十岁时,老师在算数课上出了一道难题:“把1到100的整数写下来,然后把它们加起来!”每当有考试时他们有如下的习惯:第一个做完的就把石板(当时通行,写字用)面朝下地放在老师的桌子上,第二个做完的就把石板摆在第一张石板上,就这样一个一个摞起来。这个难题当然难不倒学过算数级数的人,但这些孩子才刚开始学算数呢!老师心想他可以休息一下了。但他错了,因为还不到几秒钟,高斯已经把石板放在讲桌上了,同时说道:“答案在这儿!”其他的学生把数字一个个加起来,额头都出了汗水,但高斯却静静坐着,对老师投来的轻蔑的、怀疑的眼光毫不在意。考完后,老师一张张地检查着石板。大部分都做错了,学生就吃了一顿鞭打。
最后,高斯的石板被翻了过来,只见上面只有一个数字:5050(用不着说,这是正确的答案)。老师吃了一惊,高斯就解释他如何找到答案:1+100=101,2+99=101,3+98=101,??,49+52=101,50+51=101,一共有50对和为101的数目,所以答案是50×101=5050。由此可见高斯找到了算术级数的对称性,然后就像求得一般算术级数和的过程一样,把数目一对对地凑在一起。
(二)数论上的“1+2”问题
我国著名数学家陈景润(1933—1996),出生于福州市。在家里排行老三,母亲生了12个孩子,只有6个存活下来。据陈景润回忆说:“在家里我是一个多余的孩子,在学校是一只丑小鸭。但我觉得,一个人不在于外表怎样,而在于志向的高下。”(《工人日报》1989年12月18日)
陈景润从小喜欢数学,抗日战争时期升入初中的时候,从远方的沦陷区搬迁到福州的大学教师也在这个学校兼点课。他特别喜欢两个兼课的数理老师。老师也喜欢他学习善动脑筋。
陈景润在读高中时,教他的数学老师沈元是当时清华大学航空系的系主任(现为北航教授)。沈老师知识渊博,诲人不倦。
有一天,沈老师向全班学生讲了哥德巴赫(C.Goldbach,1690—1764)的故事:“1742年,德国数学家哥德巴赫写了一封信给著名数学家欧拉,提出了一个难题。他发现‘每一个偶数(除2以外)都可以写成两个素数的和’(简称为“1+1”),如4=2+2,6=3+3,8=5+3,10=7+3,??。欧拉想了许久没有解决。有人对一个一个的偶数进行了这样的验算,一直验算到三亿三千万都表明是对的。但是更大更大的数目呢?猜想起来也是对 的,猜想应当证明,要证明却是很难很难的。二百多年过去了,至今尚未解决,”接着沈老师笑着说:“我有一天夜里,梦见我的一个学生证明了这个哥德巴赫猜想。”同学们听罢都笑了,只有陈景润一人没有笑。
陈景润把这个故事深深地记在心里,为解决这个难题,他坚持不懈地计算了20多年,于1966年5月在《科学通报》第17期上证明了“1+2”问题,就是说:任何一个大偶数等于一个素数与另一个不超过两个素数之积的和。这被国外誉为“陈氏定理”。这就是数论上“1+2”问题。
虽然“1+1”问题(哥德巴赫猜想)至今未被解决,但陈景润对它的最终被解决作出了重要贡献。
