17.1 勾股定理(2)课件
图片预览





文档简介
人教版数学八年级下册
17.1勾股定理(2)
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
复习回顾:
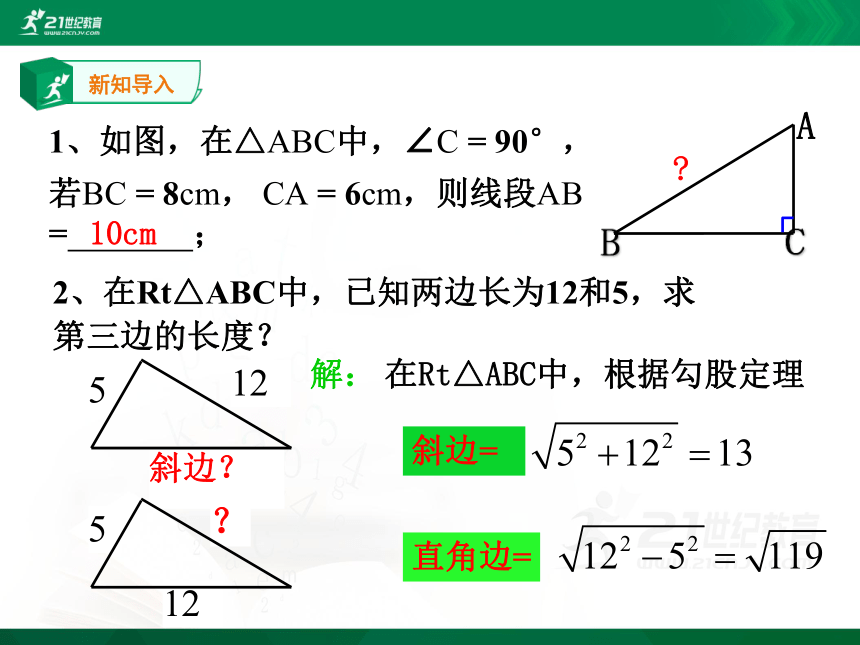
1、如图,在△ABC中,∠C = 90°,
若BC = 8cm, CA = 6cm,则线段AB = ;
2、在Rt△ABC中,已知两边长为12和5,求
第三边的长度?
10cm
?
解:
在Rt△ABC中,根据勾股定理
斜边=
直角边=
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
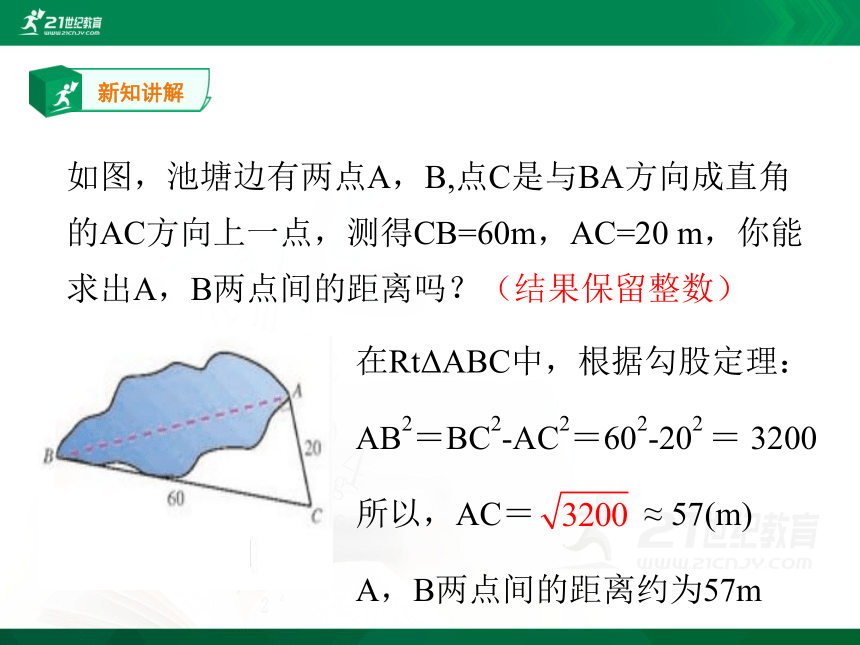
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗?(结果保留整数)
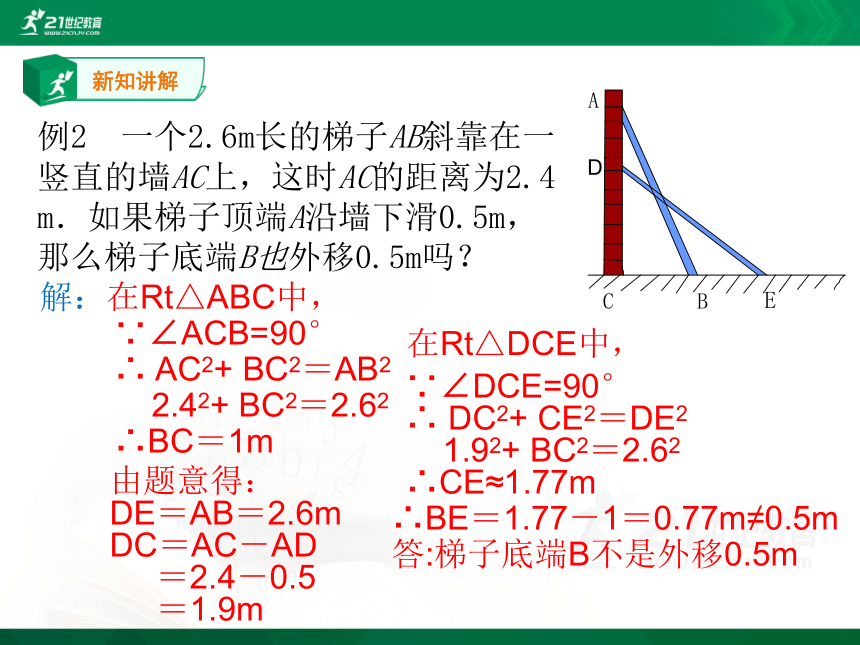
例2 一个2.6m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4
m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.62
∴BC=1m
由题意得:
DE=AB=2.6m
DC=AC-AD
=2.4-0.5
=1.9m
在Rt△DCE中,
∴BE=1.77-1=0.77m≠0.5m
答:梯子底端B不是外移0.5m
∵∠DCE=90°
∴ DC2+ CE2=DE2
1.92+ BC2=2.62
∴CE≈1.77m
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设水池的深度AC为x米,则芦苇高AD为 (x+1)米.
根据题意得:
BC2+AC2=AB2
∴52+x2 =(x+1)2
25+x2=x2+2x+1
x=12
∴x+1=12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型(勾股定理),运用
相应的数学知识;
(3)方程思想在本题中的运用.
利用勾股定理解决实际问题的一般思路:
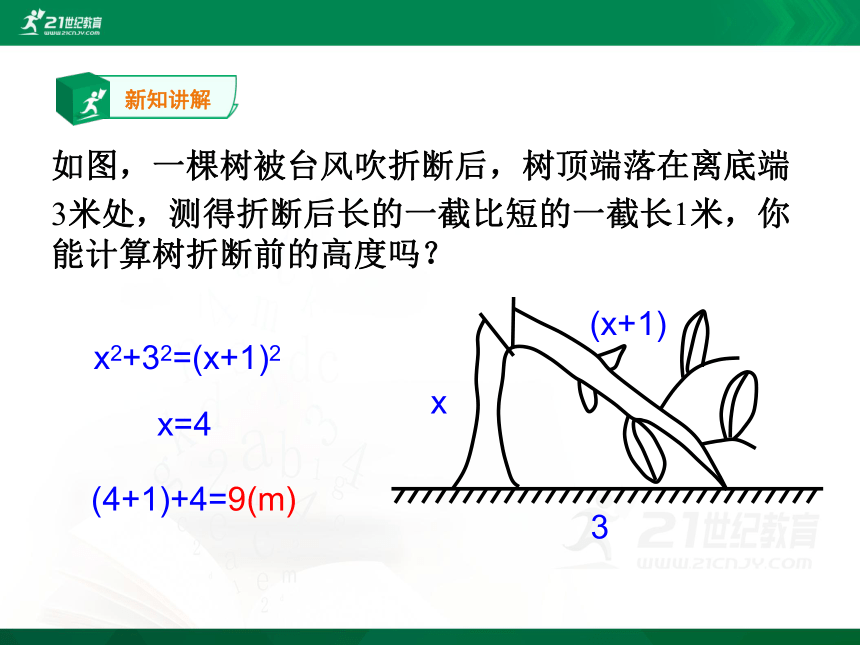
如图,一棵树被台风吹折断后,树顶端落在离底端
3米处,测得折断后长的一截比短的一截长1米,你能计算树折断前的高度吗?
x2+32=(x+1)2
x=4
(4+1)+4=9(m)
例4 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x
25-x
解:设AE= x km,则BE=
(25-x)km.
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴ x=10
有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中, ∠B=90°, AB=BC=50,
∴由勾股定理可知:
例5 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。
帮卡车司机排忧解难。
O
┏
C
D
H
实际问题
数学问题
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度与CH值的大小关系。
当车的高度﹥CH时,则车 通过 当车的高度﹤CH时,则车 通过
不能
能
由图可知:CH=DH+CD OD=0.8米,OC= 1米 ,CD⊥AB, 于是车能否通过这个问题就转化到直角△ODC中CD这条边上;
∵2.3+0.6=2.9>2.5
∴卡车能通过厂门。
例6 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
5
12
∵ AB2=AC2+BC2=169,
∴ AB=13.
例7 有一圆形油罐底面圆的周长为8m,高为2m,一只老鼠从A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
C
B
2
4
解:
如平面展开图所示.
在Rt△ABC中,根据勾股定理
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形.
小结:在最短路径问题中,通常都要用到“两点之间,线段最短”这个原理。
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”或者“垂线段最短”等性质来解决问题。
1.在实际问题中建立直角三角形模型,利用勾股定理解决问题。
1.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.
2.学校有一块长方形的花圃,经常有同学为了少走几步而走捷径,于是在草坪上开辟了一条“新路”,他们这样走少走了几步?(每两步约为1米)
130
10步
3.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
16米
6.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高______米。
15
4.一架5m长的梯子,斜立靠在一竖直的墙上,这是梯子下端距离墙的底端3m,若梯子顶端下滑了1m,则梯子底端将外移 。
1m
5.如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需 米。
7
7.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的
水平距离为2米,问这里水深是__ m。
8.小明想知道学校旗杆的高,他发现旗杆顶端的绳子
垂到地面还多1米,当他把绳子的下端拉开5米后,
发现下端刚好接触地面,求旗杆的高度。
12米
9.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.
10.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是_________.
25dm
11.有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长12m处,即AB长为最短路线.
12.如果蚂蚁处于的位置是一个长、宽、高分别为5、4、3的长方体的左下端A,它到右上端B的最短路线是多长呢?
13.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
能
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.1勾股定理(2)
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
复习回顾:
1、如图,在△ABC中,∠C = 90°,
若BC = 8cm, CA = 6cm,则线段AB = ;
2、在Rt△ABC中,已知两边长为12和5,求
第三边的长度?
10cm
?
解:
在Rt△ABC中,根据勾股定理
斜边=
直角边=
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗?(结果保留整数)
例2 一个2.6m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4
m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.62
∴BC=1m
由题意得:
DE=AB=2.6m
DC=AC-AD
=2.4-0.5
=1.9m
在Rt△DCE中,
∴BE=1.77-1=0.77m≠0.5m
答:梯子底端B不是外移0.5m
∵∠DCE=90°
∴ DC2+ CE2=DE2
1.92+ BC2=2.62
∴CE≈1.77m
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设水池的深度AC为x米,则芦苇高AD为 (x+1)米.
根据题意得:
BC2+AC2=AB2
∴52+x2 =(x+1)2
25+x2=x2+2x+1
x=12
∴x+1=12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型(勾股定理),运用
相应的数学知识;
(3)方程思想在本题中的运用.
利用勾股定理解决实际问题的一般思路:
如图,一棵树被台风吹折断后,树顶端落在离底端
3米处,测得折断后长的一截比短的一截长1米,你能计算树折断前的高度吗?
x2+32=(x+1)2
x=4
(4+1)+4=9(m)
例4 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x
25-x
解:设AE= x km,则BE=
(25-x)km.
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴ x=10
有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中, ∠B=90°, AB=BC=50,
∴由勾股定理可知:
例5 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。
帮卡车司机排忧解难。
O
┏
C
D
H
实际问题
数学问题
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度与CH值的大小关系。
当车的高度﹥CH时,则车 通过 当车的高度﹤CH时,则车 通过
不能
能
由图可知:CH=DH+CD OD=0.8米,OC= 1米 ,CD⊥AB, 于是车能否通过这个问题就转化到直角△ODC中CD这条边上;
∵2.3+0.6=2.9>2.5
∴卡车能通过厂门。
例6 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
5
12
∵ AB2=AC2+BC2=169,
∴ AB=13.
例7 有一圆形油罐底面圆的周长为8m,高为2m,一只老鼠从A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
C
B
2
4
解:
如平面展开图所示.
在Rt△ABC中,根据勾股定理
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形.
小结:在最短路径问题中,通常都要用到“两点之间,线段最短”这个原理。
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”或者“垂线段最短”等性质来解决问题。
1.在实际问题中建立直角三角形模型,利用勾股定理解决问题。
1.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.
2.学校有一块长方形的花圃,经常有同学为了少走几步而走捷径,于是在草坪上开辟了一条“新路”,他们这样走少走了几步?(每两步约为1米)
130
10步
3.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
16米
6.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高______米。
15
4.一架5m长的梯子,斜立靠在一竖直的墙上,这是梯子下端距离墙的底端3m,若梯子顶端下滑了1m,则梯子底端将外移 。
1m
5.如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需 米。
7
7.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的
水平距离为2米,问这里水深是__ m。
8.小明想知道学校旗杆的高,他发现旗杆顶端的绳子
垂到地面还多1米,当他把绳子的下端拉开5米后,
发现下端刚好接触地面,求旗杆的高度。
12米
9.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.
10.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是_________.
25dm
11.有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长12m处,即AB长为最短路线.
12.如果蚂蚁处于的位置是一个长、宽、高分别为5、4、3的长方体的左下端A,它到右上端B的最短路线是多长呢?
13.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
能
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
