六年级下册数学一课一练3.1圆柱 人教新课标(含答案)
文档属性
| 名称 | 六年级下册数学一课一练3.1圆柱 人教新课标(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-07 07:21:10 | ||
图片预览


文档简介
六年级下册数学一课一练-3.1圆柱
一、单选题
1.计算做一个圆柱形烟囱需要多少铁皮,就是求它的(? ?)。
A.?底面积???????????????????????????????B.?侧面积???????????????????????????????C.?底面积和侧面积之和
2.当一个圆柱的底面________和高相等时,展开这个圆柱的侧面,可以得到一个正方形.(?? )
A.?直径?????????????????????????????????????????B.?半径?????????????????????????????????????????C.?周长
3.圆柱的底面半径是r , 高是h , 它的表面积可以用式子(?? )来表示.
A.??????????????????????????????B.???????????????????????????????C.?
4.一个圆柱的底面半径扩大4倍,高不变,它的体积扩大(?? )
A.?4倍????????????????????????????????????????B.?8倍??????????????????????????????????????????C.?16倍
5.一个圆柱的底面半径2厘米,高3厘米.它的表面积是(? )平方厘米.
A.?62.8 ?????????????????????????????????????B.?31.4 ?????????????????????????????????????C.?78.5
6.下面各图是圆柱的展开图的是( ??)。
A.???????????B.???????????C.???????????D.?
7.将圆柱的侧面展开,得到的平面图形是(???? )
A.?圆形??????????????????????????????????B.?三角形?????????????????????????????????C.?长方形??????????????????????????????????D.?梯形
8.一个圆柱形纸筒,它的底面直径是1分米,高是3.14分米,它的侧面展开图是( )
A.?长方形???????????????????????????????????B.?正方形???????????????????????????????????C.?平行四边形
二、判断题
9.侧面积相等的两个圆柱,表面积也相等。
10.圆柱的侧面积等于底面积乘高。(??? )
11.如果圆柱的底面半径和高相等,那么它的两个底面积的和等于它的侧面积。
12.两个圆柱形水池体积相等,容积也一定相等.(判断对错)
13.一个圆柱的底面半径是r,高是2πr,那么它的侧面沿高展开是正方形。(??? )
三、填空题
14.一个长方形长3分米,宽2分米,以它的任意一边做轴旋转,能得到不同的圆柱体,其中较大的一个圆柱体的体积是________(保留π)
15.如果把一个底面直径是2分米的圆柱的侧面展开后是一 个正方形,那么圆柱的高是?________分米,侧面积是________平方分米。
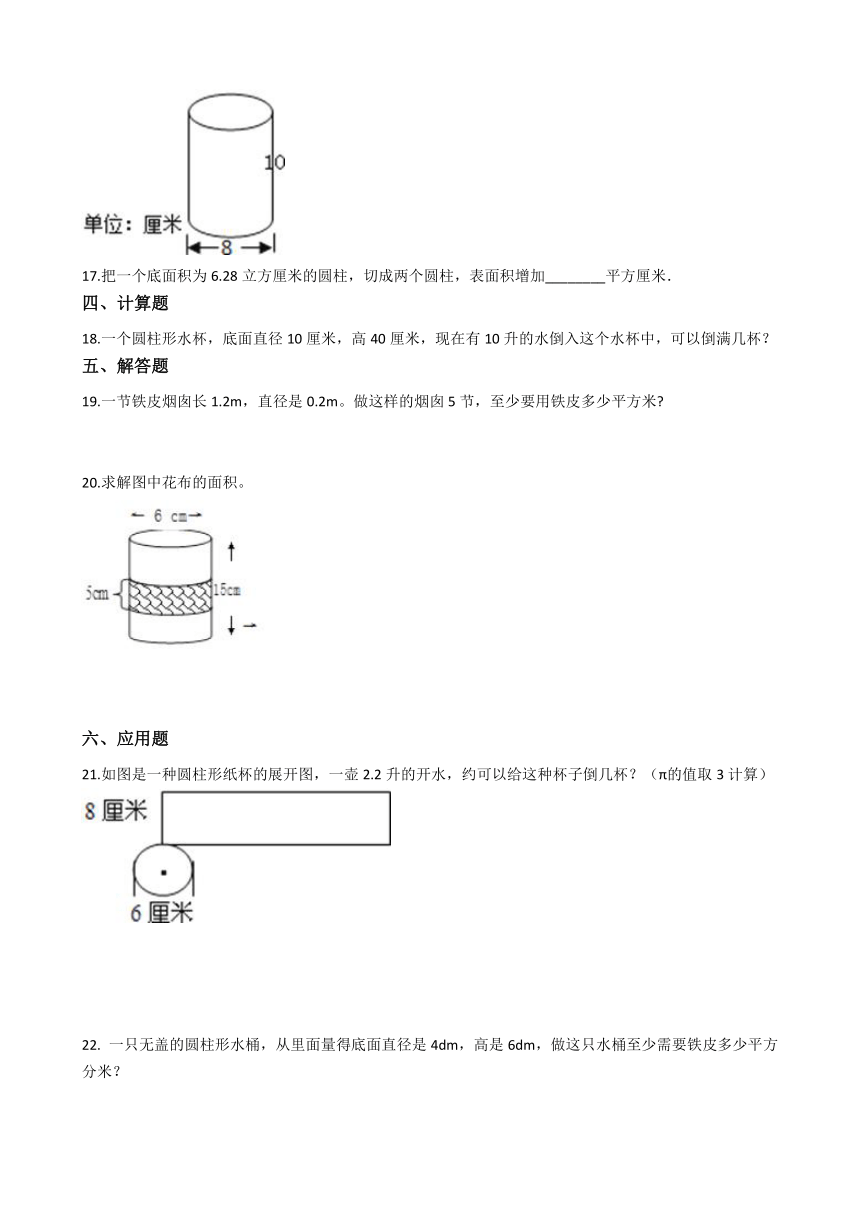
16.如图把这个圆柱的侧面展开可以得到一个长方形,这个长方形的面积是________.???
17.把一个底面积为6.28立方厘米的圆柱,切成两个圆柱,表面积增加________平方厘米.
四、计算题
18.一个圆柱形水杯,底面直径10厘米,高40厘米,现在有10升的水倒入这个水杯中,可以倒满几杯?
五、解答题
19.一节铁皮烟囱长1.2m,直径是0.2m。做这样的烟囱5节,至少要用铁皮多少平方米?
20.求解图中花布的面积。
六、应用题
21.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算)
22. 一只无盖的圆柱形水桶,从里面量得底面直径是4dm,高是6dm,做这只水桶至少需要铁皮多少平方分米?
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】解:烟囱是不需要两个底的,所以计算做一个圆柱形烟囱需要多少铁皮,就是求它的侧面积。 故答案为:B。
【分析】烟囱是不需要两个底的。
2.【答案】C
【解析】【解答】圆柱的侧面展开后如果是一个正方形,说明圆柱的底面周长和高相等. 故答案为:C 【分析】圆柱的侧面展开是一个长方形或正方形,长方形或正方形的一条边的长度与底面周长相等,另一条边的长度与高相等;如果底面周长与高相等时才是正方形.
3.【答案】A
【解析】【解答】2个底面积:πr2×2=2πr2;侧面积:2πrh;表面积:2πr2+2πrh. 故答案为:A 【分析】圆柱的表面积包括两个圆形的底面和一个侧面,圆形的底面根据圆面积公式计算,侧面积用底面周长乘高来计算.
4.【答案】C
【解析】【解答】解:原来的体积:v=πr2h,
扩大后的体积:v1=π(4r)2h=16πr2h,
体积扩大:16πr2h÷πr2h=16倍,
于是可得:它的体积扩大16倍.
故选:C.
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为v,扩大后的体积为v1 , 则扩大后的半径为4r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数.
5.【答案】A
【解析】【解答】圆柱的表面积:3.14×22×2+2×3.14×2×3
=3.14×4×2+37.68
=25.12+37.68
=62.8(平方厘米)
答:它的表面积是62.8平方厘米。
【分析】首先明确条件,已知“圆柱的底面半径是2厘米,高是3厘米”,再分别根据公式解答,它的表面积=底面积×2+侧面积,列式解答。
故答案为:A
6.【答案】C
【解析】【解答】选项A,圆柱的底面周长:3.14×6=18.84,图中长方形的长是9.42,所以不是圆柱的侧面展开图; 选项B,圆柱的底面周长:3.14×6=18.84,图中长方形的长是24,所以不是圆柱的侧面展开图; 选项C,圆柱的底面周长:3.14×6=18.84,图中长方形的长是18.84,所以是圆柱的侧面展开图; 选项D,圆柱的底面周长:3.14×6=18.84,图中长方形的长是28.26,所以不是圆柱的侧面展开图. 故答案为:C.
【分析】根据圆柱展开图的特点,圆柱沿高展开,其侧面是一个长方形,长是圆柱底面的周长,由此即可解决问题.
7.【答案】C
【解析】【解答】解:如果沿着圆柱的一条高剪开后就会得到一个长方形. 故答案为:C
【分析】沿着圆柱的高剪开后会得到一个长方形,也会得到一个正方形,如果斜着剪开还会得到一个平行四边形,由此选择即可.
8.【答案】B
【解析】【解答】解:因为3.14×1=3.14(分米);
所以它的侧面展开图是正方形;
故选:B.
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,利用圆的周长公式求出这个纸筒的底面周长,再与其高比较大小,即可知道它的侧面展开图是什么形状.
二、判断题
9.【答案】错误
【解析】【解答】解:侧面积相等的两个圆柱的底面周长不一定相等,所以底面积也不一定相等,表面积也不一定相等.原题说法正确. 故答案为:错误
【分析】圆柱的侧面积=底面周长×高,两个圆柱侧面积相等,不能说明底面周长相等,那么底面积就不能确定,所以无法确定表面积的大小.
10.【答案】错误
【解析】【解答】解:圆柱的侧面积=底面周长×高,原题说法错误. 故答案为:错误
【分析】圆柱的侧面沿着高展开后是一个长方形,长方形的长与底面周长相等,高与圆柱的高相等,所以圆柱的侧面积=底面周长×高.
11.【答案】正确
【解析】【解答】解:设底面半径为r,那么高也为r。 ?两个底面积=;侧面积==。 故答案为:正确。
【分析】圆柱两个底面积是两个等圆的面积,根据底面半径可求两个底面积;侧面是一个长方形:长是底面圆的周长,宽是高r,面积=长宽。据此可求解。
12.【答案】错误
【解析】【解答】解:两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等. 因此,两个圆柱形水池体积相等,容积也一定相等.这种说法是错误的. 故答案为:错误. 【分析】根据体积、容器的意义,物体所占空间的大小叫做物体的体积.某容器所能容纳别的物体的体积叫做这个容器的容积.两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等.据此判断.
13.【答案】正确
【解析】【解答】解:底面周长:2πr,底面周长和高相等,它的侧面沿高展开是正方形,原题说法正确. 故答案为:正确
【分析】圆柱的侧面沿着高展开后会得到一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,另一条边与圆柱的高相等;如果底面周长和高相等时,圆柱的侧面展开是正方形.
三、填空题
14.【答案】18π立方分米
【解析】【解答】解:π×32×2 =π×9×2 =18π(立方分米) 答:较大的一个圆柱的体积是18π立方分米. 故答案为:18π立方分米. 【分析】为圆柱的体积公式是:V=sh=πr2h,所以要使圆柱的体积最大,必须让半径尽可能的大;根据本题意知道,要使得到的圆柱的体积最大,那必须以宽2分米为轴旋转,即得到的圆柱的底面半径是3分米,高是2分米,由此根据圆柱的体积公式,代入数据,解答即可.
15.【答案】2π ;4π2
【解析】【解答】本题圆柱的高就等于圆柱的底面周长,为2π , 侧面积为2π×2π=4π2。
【分析】圆柱的侧面积就等于圆柱的底面周长乘以高。
16.【答案】80π平方厘米
【解析】【解答】π×8×10,
=π×80,
=80π(平方厘米);
答:这个长方形的面积是80π平方厘米.
故答案为:80π平方厘米。
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:求长方形的面积,即圆柱的侧面积,根据“圆柱的侧面积=πdh“解答即可。
17.【答案】12.56
【解析】【解答】6.28×2=12.56(平方厘米);
答:表面积增加列12.56平方厘米。
故答案为:12.56。
【分析】一个圆柱截成同样长的二段,增加两个相等底面,据此解答。
四、计算题
18.【答案】解答: 3.14×(10÷2)2×40
=3.14×1000
=3140(立方厘米)
=3.14(升)
10÷3.14≈3(杯〕
答:可以倒满3杯。
【解析】【分析】先依据圆柱的容积的计算方法,求出圆柱形水杯的容积,再根据除法的意义,用水的总量除以圆柱形水杯的容积,问题即可得解。
五、解答题
19.【答案】解:1.2×0.2×3.14×5=3.768(平方米) 答:至少要用铁皮3.768平方米。
【解析】【分析】烟囱是没有底的圆柱:一节铁皮烟囱的面积=烟囱长烟囱底面周长。烟囱底面周长=d, 求5个一节铁皮烟囱的面积是多少,据此可求解。
20.【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【解析】【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
六、应用题
21.【答案】解:纸杯的底面半径为:6÷2=3(厘米),
纸杯的容积为:3×32×8
=27×8,
=216(立方厘米),
216立方厘米=0.216立方分米=0.216升,
2.2÷0.216≈10(杯);
答:约可以给这种杯子倒10杯水。
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案。
22.【答案】解:3.14×4×6+3.14×(4÷2)2 =75.36+3.14×4 =75.36+12.56 =87.92(平方分米), 答:至少需要铁皮87.92平方米.
【解析】【分析】圆柱形铁皮水桶无盖,只需要计算一个底面和侧面的面积,由圆柱体侧面积和圆的面积计算方法列式解答即可.
一、单选题
1.计算做一个圆柱形烟囱需要多少铁皮,就是求它的(? ?)。
A.?底面积???????????????????????????????B.?侧面积???????????????????????????????C.?底面积和侧面积之和
2.当一个圆柱的底面________和高相等时,展开这个圆柱的侧面,可以得到一个正方形.(?? )
A.?直径?????????????????????????????????????????B.?半径?????????????????????????????????????????C.?周长
3.圆柱的底面半径是r , 高是h , 它的表面积可以用式子(?? )来表示.
A.??????????????????????????????B.???????????????????????????????C.?
4.一个圆柱的底面半径扩大4倍,高不变,它的体积扩大(?? )
A.?4倍????????????????????????????????????????B.?8倍??????????????????????????????????????????C.?16倍
5.一个圆柱的底面半径2厘米,高3厘米.它的表面积是(? )平方厘米.
A.?62.8 ?????????????????????????????????????B.?31.4 ?????????????????????????????????????C.?78.5
6.下面各图是圆柱的展开图的是( ??)。
A.???????????B.???????????C.???????????D.?
7.将圆柱的侧面展开,得到的平面图形是(???? )
A.?圆形??????????????????????????????????B.?三角形?????????????????????????????????C.?长方形??????????????????????????????????D.?梯形
8.一个圆柱形纸筒,它的底面直径是1分米,高是3.14分米,它的侧面展开图是( )
A.?长方形???????????????????????????????????B.?正方形???????????????????????????????????C.?平行四边形
二、判断题
9.侧面积相等的两个圆柱,表面积也相等。
10.圆柱的侧面积等于底面积乘高。(??? )
11.如果圆柱的底面半径和高相等,那么它的两个底面积的和等于它的侧面积。
12.两个圆柱形水池体积相等,容积也一定相等.(判断对错)
13.一个圆柱的底面半径是r,高是2πr,那么它的侧面沿高展开是正方形。(??? )
三、填空题
14.一个长方形长3分米,宽2分米,以它的任意一边做轴旋转,能得到不同的圆柱体,其中较大的一个圆柱体的体积是________(保留π)
15.如果把一个底面直径是2分米的圆柱的侧面展开后是一 个正方形,那么圆柱的高是?________分米,侧面积是________平方分米。
16.如图把这个圆柱的侧面展开可以得到一个长方形,这个长方形的面积是________.???
17.把一个底面积为6.28立方厘米的圆柱,切成两个圆柱,表面积增加________平方厘米.
四、计算题
18.一个圆柱形水杯,底面直径10厘米,高40厘米,现在有10升的水倒入这个水杯中,可以倒满几杯?
五、解答题
19.一节铁皮烟囱长1.2m,直径是0.2m。做这样的烟囱5节,至少要用铁皮多少平方米?
20.求解图中花布的面积。
六、应用题
21.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算)
22. 一只无盖的圆柱形水桶,从里面量得底面直径是4dm,高是6dm,做这只水桶至少需要铁皮多少平方分米?
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】解:烟囱是不需要两个底的,所以计算做一个圆柱形烟囱需要多少铁皮,就是求它的侧面积。 故答案为:B。
【分析】烟囱是不需要两个底的。
2.【答案】C
【解析】【解答】圆柱的侧面展开后如果是一个正方形,说明圆柱的底面周长和高相等. 故答案为:C 【分析】圆柱的侧面展开是一个长方形或正方形,长方形或正方形的一条边的长度与底面周长相等,另一条边的长度与高相等;如果底面周长与高相等时才是正方形.
3.【答案】A
【解析】【解答】2个底面积:πr2×2=2πr2;侧面积:2πrh;表面积:2πr2+2πrh. 故答案为:A 【分析】圆柱的表面积包括两个圆形的底面和一个侧面,圆形的底面根据圆面积公式计算,侧面积用底面周长乘高来计算.
4.【答案】C
【解析】【解答】解:原来的体积:v=πr2h,
扩大后的体积:v1=π(4r)2h=16πr2h,
体积扩大:16πr2h÷πr2h=16倍,
于是可得:它的体积扩大16倍.
故选:C.
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为v,扩大后的体积为v1 , 则扩大后的半径为4r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数.
5.【答案】A
【解析】【解答】圆柱的表面积:3.14×22×2+2×3.14×2×3
=3.14×4×2+37.68
=25.12+37.68
=62.8(平方厘米)
答:它的表面积是62.8平方厘米。
【分析】首先明确条件,已知“圆柱的底面半径是2厘米,高是3厘米”,再分别根据公式解答,它的表面积=底面积×2+侧面积,列式解答。
故答案为:A
6.【答案】C
【解析】【解答】选项A,圆柱的底面周长:3.14×6=18.84,图中长方形的长是9.42,所以不是圆柱的侧面展开图; 选项B,圆柱的底面周长:3.14×6=18.84,图中长方形的长是24,所以不是圆柱的侧面展开图; 选项C,圆柱的底面周长:3.14×6=18.84,图中长方形的长是18.84,所以是圆柱的侧面展开图; 选项D,圆柱的底面周长:3.14×6=18.84,图中长方形的长是28.26,所以不是圆柱的侧面展开图. 故答案为:C.
【分析】根据圆柱展开图的特点,圆柱沿高展开,其侧面是一个长方形,长是圆柱底面的周长,由此即可解决问题.
7.【答案】C
【解析】【解答】解:如果沿着圆柱的一条高剪开后就会得到一个长方形. 故答案为:C
【分析】沿着圆柱的高剪开后会得到一个长方形,也会得到一个正方形,如果斜着剪开还会得到一个平行四边形,由此选择即可.
8.【答案】B
【解析】【解答】解:因为3.14×1=3.14(分米);
所以它的侧面展开图是正方形;
故选:B.
【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,利用圆的周长公式求出这个纸筒的底面周长,再与其高比较大小,即可知道它的侧面展开图是什么形状.
二、判断题
9.【答案】错误
【解析】【解答】解:侧面积相等的两个圆柱的底面周长不一定相等,所以底面积也不一定相等,表面积也不一定相等.原题说法正确. 故答案为:错误
【分析】圆柱的侧面积=底面周长×高,两个圆柱侧面积相等,不能说明底面周长相等,那么底面积就不能确定,所以无法确定表面积的大小.
10.【答案】错误
【解析】【解答】解:圆柱的侧面积=底面周长×高,原题说法错误. 故答案为:错误
【分析】圆柱的侧面沿着高展开后是一个长方形,长方形的长与底面周长相等,高与圆柱的高相等,所以圆柱的侧面积=底面周长×高.
11.【答案】正确
【解析】【解答】解:设底面半径为r,那么高也为r。 ?两个底面积=;侧面积==。 故答案为:正确。
【分析】圆柱两个底面积是两个等圆的面积,根据底面半径可求两个底面积;侧面是一个长方形:长是底面圆的周长,宽是高r,面积=长宽。据此可求解。
12.【答案】错误
【解析】【解答】解:两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等. 因此,两个圆柱形水池体积相等,容积也一定相等.这种说法是错误的. 故答案为:错误. 【分析】根据体积、容器的意义,物体所占空间的大小叫做物体的体积.某容器所能容纳别的物体的体积叫做这个容器的容积.两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等.据此判断.
13.【答案】正确
【解析】【解答】解:底面周长:2πr,底面周长和高相等,它的侧面沿高展开是正方形,原题说法正确. 故答案为:正确
【分析】圆柱的侧面沿着高展开后会得到一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,另一条边与圆柱的高相等;如果底面周长和高相等时,圆柱的侧面展开是正方形.
三、填空题
14.【答案】18π立方分米
【解析】【解答】解:π×32×2 =π×9×2 =18π(立方分米) 答:较大的一个圆柱的体积是18π立方分米. 故答案为:18π立方分米. 【分析】为圆柱的体积公式是:V=sh=πr2h,所以要使圆柱的体积最大,必须让半径尽可能的大;根据本题意知道,要使得到的圆柱的体积最大,那必须以宽2分米为轴旋转,即得到的圆柱的底面半径是3分米,高是2分米,由此根据圆柱的体积公式,代入数据,解答即可.
15.【答案】2π ;4π2
【解析】【解答】本题圆柱的高就等于圆柱的底面周长,为2π , 侧面积为2π×2π=4π2。
【分析】圆柱的侧面积就等于圆柱的底面周长乘以高。
16.【答案】80π平方厘米
【解析】【解答】π×8×10,
=π×80,
=80π(平方厘米);
答:这个长方形的面积是80π平方厘米.
故答案为:80π平方厘米。
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:求长方形的面积,即圆柱的侧面积,根据“圆柱的侧面积=πdh“解答即可。
17.【答案】12.56
【解析】【解答】6.28×2=12.56(平方厘米);
答:表面积增加列12.56平方厘米。
故答案为:12.56。
【分析】一个圆柱截成同样长的二段,增加两个相等底面,据此解答。
四、计算题
18.【答案】解答: 3.14×(10÷2)2×40
=3.14×1000
=3140(立方厘米)
=3.14(升)
10÷3.14≈3(杯〕
答:可以倒满3杯。
【解析】【分析】先依据圆柱的容积的计算方法,求出圆柱形水杯的容积,再根据除法的意义,用水的总量除以圆柱形水杯的容积,问题即可得解。
五、解答题
19.【答案】解:1.2×0.2×3.14×5=3.768(平方米) 答:至少要用铁皮3.768平方米。
【解析】【分析】烟囱是没有底的圆柱:一节铁皮烟囱的面积=烟囱长烟囱底面周长。烟囱底面周长=d, 求5个一节铁皮烟囱的面积是多少,据此可求解。
20.【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【解析】【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
六、应用题
21.【答案】解:纸杯的底面半径为:6÷2=3(厘米),
纸杯的容积为:3×32×8
=27×8,
=216(立方厘米),
216立方厘米=0.216立方分米=0.216升,
2.2÷0.216≈10(杯);
答:约可以给这种杯子倒10杯水。
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案。
22.【答案】解:3.14×4×6+3.14×(4÷2)2 =75.36+3.14×4 =75.36+12.56 =87.92(平方分米), 答:至少需要铁皮87.92平方米.
【解析】【分析】圆柱形铁皮水桶无盖,只需要计算一个底面和侧面的面积,由圆柱体侧面积和圆的面积计算方法列式解答即可.
