六年级下册数学一课一练3.2圆锥 人教新课标(含答案)
文档属性
| 名称 | 六年级下册数学一课一练3.2圆锥 人教新课标(含答案) | 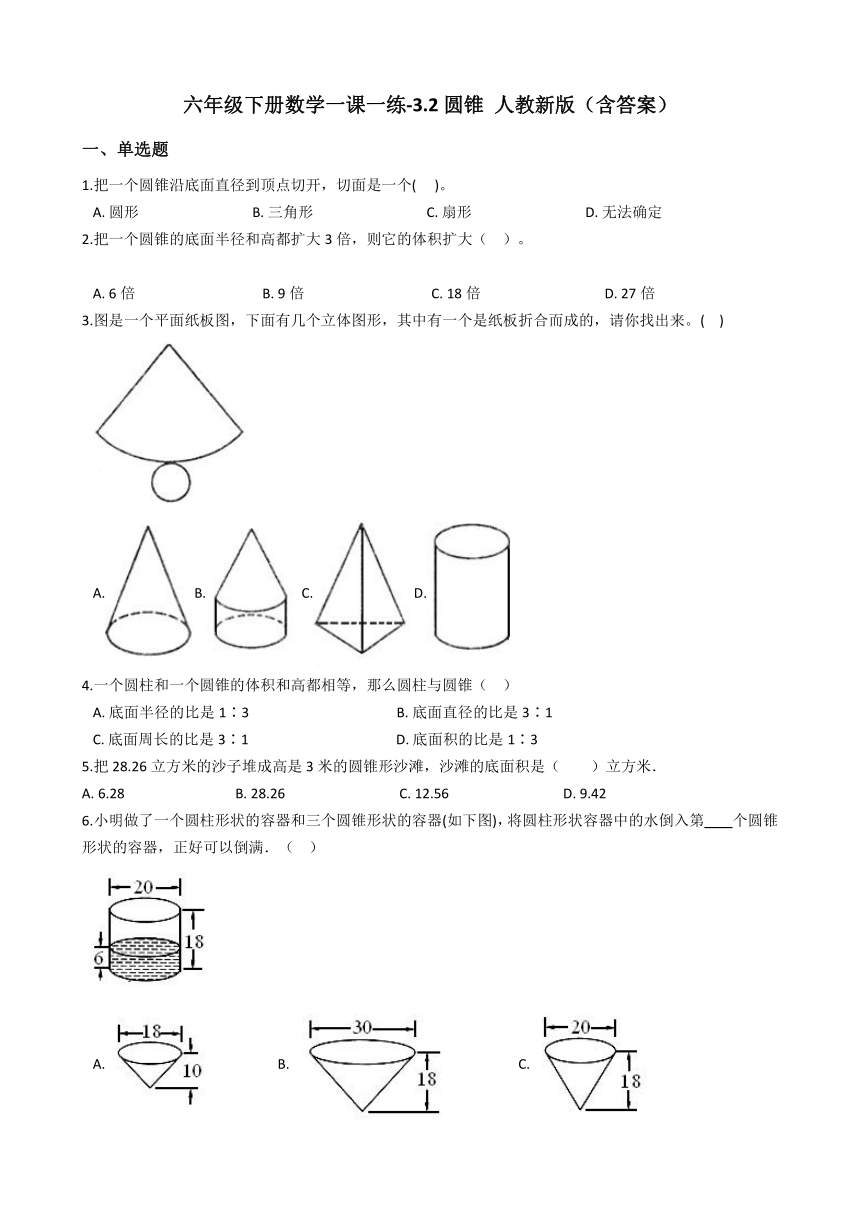 | |
| 格式 | zip | ||
| 文件大小 | 61.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-07 07:22:05 | ||
图片预览




文档简介
六年级下册数学一课一练-3.2圆锥 人教新版(含答案)
一、单选题
1.把一个圆锥沿底面直径到顶点切开,切面是一个(??? )。
A.?圆形?????????????????????????????????B.?三角形?????????????????????????????????C.?扇形?????????????????????????????????D.?无法确定
2.把一个圆锥的底面半径和高都扩大3倍,则它的体积扩大( ??)。
A.?6倍?????????????????????????????????????B.?9倍?????????????????????????????????????C.?18倍????????????????????????????????????D.?27倍
3.图是一个平面纸板图,下面有几个立体图形,其中有一个是纸板折合而成的,请你找出来。(?? )
A.B.C.D.
4.一个圆柱和一个圆锥的体积和高都相等,那么圆柱与圆锥(?? )
A.?底面半径的比是1∶3???????????????????????????????????????????B.?底面直径的比是3∶1 C.?底面周长的比是3∶1???????????????????????????????????????????D.?底面积的比是1∶3
5.把28.26立方米的沙子堆成高是3米的圆锥形沙滩,沙滩的底面积是( )立方米.
A.?6.28 ??????????????????????????????B.?28.26 ???????????????????????????????C.?12.56 ???????????????????????????????D.?9.42
6.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第 ??????个圆锥形状的容器,正好可以倒满.(?? )
A.?????????????????????B.?????????????????????C.?
7.圆锥的底面半径扩大4倍,高不变,体积扩大(? )倍.
A.?4 ?????????????????????????????????????????B.?16 ?????????????????????????????????????????C.?8
二、判断题
8.一个圆锥的体积是9.42 ,底面半径是3dm,求它的高的算式是:h=9.42÷(3.14× )×
9.如果一个圆锥的体积是一个圆柱体积的3倍,它们的底面积相等,那么圆锥的高一定是圆柱高的9倍。
10.圆锥的体积等于圆柱体积的三分之一.
11.圆锥有无数条高。
12.从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形。
三、填空题
13.一个圆锥和一个圆柱的体积相等,底面积也相等.这个圆锥的高是圆柱的高的________倍.
14.一个圆锥和一个圆柱等底等高,圆锥体积比圆柱体积少________?.
15.两个高相等,底面半径之比是1:2的圆柱与圆锥,它们的体积之比是________.
16.一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆柱体的高6厘米,那么圆锥体的高是 ________厘米。
17.计算下面圆锥的体积是________? .
四、计算题
18.把一个体积是282.6立方厘米的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件,求圆锥零件的高?(π取3.14)
五、解答题
19.怎样测量一个圆锥的高?
20.一个直角三角形,绕它的一条直角边旋转一周,形成了一个底面半径4厘米、高3厘米的圆锥
(1)画出这个直角三角形,并标出是绕哪条直角边旋转的.
(2)这个圆锥的体积是多少立方厘米?
六、应用题
21.一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重1.5吨,这堆沙重多少吨??? ??
22.一个圆锥形沙堆,底面积是9.42平方米,高0.9米,把这堆沙子铺入长4.5米,宽2米的沙坑里,可以铺多厚?
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】解:把一个圆锥沿底面直径到顶点切开,切面是一个三角形. 故答案为:B
【分析】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
2.【答案】D
【解析】【解答】把一个圆锥的底面半径和高都扩大3倍,则它的体积扩大:3×3×3=27倍. 故答案为:D.
【分析】根据圆锥的体积公式:圆锥的体积V=πr2h,据此分析解答即可.
3.【答案】A
【解析】【解答】解:A、是圆锥,符合题意;B、C、D都不是圆锥,不符合题意。 故答案为:A。
【分析】观察展开图,这个图形下面是圆形,侧面展开后是一个扇形,这是圆锥的展开图,由此判断并选择即可。
4.【答案】D
【解析】【解答】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,也就是说圆柱与圆锥的底面积之比是1:3。 故答案为:D。 【分析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
5.【答案】B
【解析】【解答】解:28.26÷ ÷3=28.26(平方米),
答:沙堆的底面积是28.26平方米.
故选:B.
【分析】根据圆锥的体积公式:V= sh可计算出圆锥的底面积,即用沙子的体积除以再除以高即可得到答案.
6.【答案】C
【解析】【解答】3.14×(20÷2)2×6=1884,×3.14×(20÷2)2×18=1884 故答案为:C。
【分析】解答此题先用圆柱的体积公式求出水的体积,然后求出圆锥的体积,找到和圆柱内水的体积相同的圆锥的体积即可解答此题。
7.【答案】B
【解析】【解答】解:设圆锥的底面半径为r , 高为h , 则扩大后的半径4r ,
原来的体积: πr2h ,
现在的体积: π(4r)2h= πr2h ,
体积扩大: πr2h÷ πr2h=16倍;
【分析】圆锥体的体积= ×底面积×高,设圆锥的底面半径为r,高为h,则扩大后的半径为4r,分别求出变化前后的体积,即可求得体积扩大的倍数。
故选:B
二、判断题
8.【答案】错误
【解析】【解答】圆锥的高=9.42×3÷(3.14×32) 故答案为:错误。 【分析】根据圆锥的体积公式可知,圆锥的高=体积×3÷底面积,据此结合题意分析即可。
9.【答案】正确
【解析】【解答】由题意得:圆柱的底面积×高×3=圆锥的底面积×高×,已知它们的底面积相等,所以,圆柱的高×3=圆锥的高×,即圆锥的高是圆柱高的9倍。 故答案为:正确。 【分析】由题意可得等量关系:圆柱的底面积×高×3=圆锥的底面积×高×,已知它们的底面积相等,那么由此可求得圆锥的高的是圆柱高的几倍,然后再进行判断即可。
10.【答案】错误
【解析】【解答】解:圆锥的体积等于圆柱体积的三分之一是错误的,只有在圆锥、圆柱等底、等高的情况下,圆锥的体积等于圆柱体积的三分之一. 故答案为:错误. 【分析】等底等高的圆锥体积是圆柱体积的三分之一,在没有等底等高一条件,圆锥的体积可能小于圆柱的体积,也可能等于圆柱的体积或大小圆柱的体积.圆柱和圆锥只有体积、底面积、高,这三个条件中,其中两个相等,才能比较第三个.
11.【答案】错误
【解析】【解答】圆锥只有一条高。 故答案为:错误。
【分析】圆锥只有一条高,圆锥的高是圆锥的顶点到底面圆心的距离,两点确定一条线段,因此圆锥只有一条高。
12.【答案】正确
【解析】【解答】解:根据圆锥的特征可知:从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形.原题说法正确. 故答案为:正确
【分析】从圆锥的顶点向底面垂直切割,会得到两个切面,这两个切面都是三角形且是等腰三角形.
三、填空题
13.【答案】3
【解析】【解答】一个圆锥和一个圆柱的体积相等,底面积也相等.这个圆锥的高是圆柱的高的3倍. 故答案为:3. 【分析】根据圆柱和圆锥的体积公式,圆柱的体积=底面积×高,圆锥的体积=底面积×高,当体积和底面积相等时,圆锥的高是圆柱的3倍.
14.【答案】
【解析】【解答】设圆柱和圆锥的底面积都是S,高都是h,则 圆柱体积:V=Sh; 圆锥体积:V=Sh; (Sh-Sh)÷Sh =Sh÷Sh = 故答案为:.
【分析】根据题意可知,等底等高的圆柱体积是圆锥体积的3倍,据此设出圆柱和圆锥的底面积都是S,高都是h,分别求出圆锥和圆柱的体积,然后用(圆柱的体积-圆锥的体积)÷圆柱的体积,据此列式解答.
15.【答案】3:4
【解析】【解答】假设圆柱的底面半径是1,那么圆锥的底面半径是2, V柱:V锥=(π×12h):(π×22h) ????????? =πh:πh ????????? =1: ????????? =3:4 故答案为:3:4. 【分析】由“底面半径之比是1:2”可知,假设圆柱的底面半径是1,那么圆锥的底面半径是2,可用体积的字母公式列成比来解答.
16.【答案】18
【解析】【解答】6×3=18(厘米) 故答案为:18.
【分析】一个圆柱体和一个圆锥体的底面积和体积分别相等,则圆锥的高是圆柱高的3倍,据此解答.
17.【答案】339.12
【解析】【解答】×3.14×62×9=339.12(立方厘米) 【分析】解答此题要运用圆锥的体积公式,即圆锥体积=底面积×高,然后代入数据计算即可。
四、计算题
18.【答案】解答:282.6×3÷(3.14×62)=7.5(厘米)
答:圆锥零件的高是7.5厘米。
【解析】【分析】根据题意,铁块的体积等于熔铸成的圆锥体的体积,然后再用铁块的体积乘3除以圆锥的底面积,列式解答即可得到答案。
五、解答题
19.【答案】解:方法一:
①把圆锥的底面放平;
②将一块平板水平地放在圆锥的顶点上面;
③竖直地量出乎板和底面之间的距离。所测量出的距离就是圆锥的高。
方法二:直接用直尺测量(误差大)。
方法三:仿照方法一,把圆锥的底面朝上,保持平衡,底面圆所指的刻度即为圆锥的高。
【解析】【分析】解答此题首先要明确圆锥顶点到底圆中心的距离叫高,不能用刻度尺直接测量,也可以利用一个三角板和一把刻度尺根据矩形对边平行且相等间接测量。
20.【答案】(1)解:
(2)解:50.24立方厘米
【解析】【解答】已知底面半径是4厘米,所以这个直角三角形的底是4厘米,高是3厘米,绕3厘米直角边旋转的,体积是×3.14×42=50.24(立方厘米)
【分析】根据旋转后得到的圆锥的底面半径是4厘米,高是3厘米可知,直角三角形的一条直角边是4厘米,另一条是3厘米,绕着3厘米的直角边旋转即可,根据数据进行作图即可;根据圆锥的体积公式V=sh进行计算即可得到答案。
六、应用题
21.【答案】;?( 吨) 答:这堆沙重37.68吨。?
【解析】【解答】 ;所以这堆沙重 吨。 【分析】先求沙堆的体积。
22.【答案】解:该圆锥沙堆的体积为: S·h = ×9.42×0.9 =2.826(立方米) 沙坑的底面积为:S=ab=4.5×2=9 (平方米) 则铺成的沙的高度为:2.826÷9=0.314 (米) 答:可以铺0.314米.
【解析】【分析】根据题意,已知圆锥的底面积和高,求圆锥的体积,用公式:V=Sh,然后求出沙坑的底面积,用长×宽=沙坑的底面积,然后用圆锥沙堆的体积÷沙坑的底面积=铺沙的厚度,据此解答.
一、单选题
1.把一个圆锥沿底面直径到顶点切开,切面是一个(??? )。
A.?圆形?????????????????????????????????B.?三角形?????????????????????????????????C.?扇形?????????????????????????????????D.?无法确定
2.把一个圆锥的底面半径和高都扩大3倍,则它的体积扩大( ??)。
A.?6倍?????????????????????????????????????B.?9倍?????????????????????????????????????C.?18倍????????????????????????????????????D.?27倍
3.图是一个平面纸板图,下面有几个立体图形,其中有一个是纸板折合而成的,请你找出来。(?? )
A.B.C.D.
4.一个圆柱和一个圆锥的体积和高都相等,那么圆柱与圆锥(?? )
A.?底面半径的比是1∶3???????????????????????????????????????????B.?底面直径的比是3∶1 C.?底面周长的比是3∶1???????????????????????????????????????????D.?底面积的比是1∶3
5.把28.26立方米的沙子堆成高是3米的圆锥形沙滩,沙滩的底面积是( )立方米.
A.?6.28 ??????????????????????????????B.?28.26 ???????????????????????????????C.?12.56 ???????????????????????????????D.?9.42
6.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第 ??????个圆锥形状的容器,正好可以倒满.(?? )
A.?????????????????????B.?????????????????????C.?
7.圆锥的底面半径扩大4倍,高不变,体积扩大(? )倍.
A.?4 ?????????????????????????????????????????B.?16 ?????????????????????????????????????????C.?8
二、判断题
8.一个圆锥的体积是9.42 ,底面半径是3dm,求它的高的算式是:h=9.42÷(3.14× )×
9.如果一个圆锥的体积是一个圆柱体积的3倍,它们的底面积相等,那么圆锥的高一定是圆柱高的9倍。
10.圆锥的体积等于圆柱体积的三分之一.
11.圆锥有无数条高。
12.从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形。
三、填空题
13.一个圆锥和一个圆柱的体积相等,底面积也相等.这个圆锥的高是圆柱的高的________倍.
14.一个圆锥和一个圆柱等底等高,圆锥体积比圆柱体积少________?.
15.两个高相等,底面半径之比是1:2的圆柱与圆锥,它们的体积之比是________.
16.一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆柱体的高6厘米,那么圆锥体的高是 ________厘米。
17.计算下面圆锥的体积是________? .
四、计算题
18.把一个体积是282.6立方厘米的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件,求圆锥零件的高?(π取3.14)
五、解答题
19.怎样测量一个圆锥的高?
20.一个直角三角形,绕它的一条直角边旋转一周,形成了一个底面半径4厘米、高3厘米的圆锥
(1)画出这个直角三角形,并标出是绕哪条直角边旋转的.
(2)这个圆锥的体积是多少立方厘米?
六、应用题
21.一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重1.5吨,这堆沙重多少吨??? ??
22.一个圆锥形沙堆,底面积是9.42平方米,高0.9米,把这堆沙子铺入长4.5米,宽2米的沙坑里,可以铺多厚?
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】解:把一个圆锥沿底面直径到顶点切开,切面是一个三角形. 故答案为:B
【分析】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
2.【答案】D
【解析】【解答】把一个圆锥的底面半径和高都扩大3倍,则它的体积扩大:3×3×3=27倍. 故答案为:D.
【分析】根据圆锥的体积公式:圆锥的体积V=πr2h,据此分析解答即可.
3.【答案】A
【解析】【解答】解:A、是圆锥,符合题意;B、C、D都不是圆锥,不符合题意。 故答案为:A。
【分析】观察展开图,这个图形下面是圆形,侧面展开后是一个扇形,这是圆锥的展开图,由此判断并选择即可。
4.【答案】D
【解析】【解答】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,也就是说圆柱与圆锥的底面积之比是1:3。 故答案为:D。 【分析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆柱和圆锥体积相等、高相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
5.【答案】B
【解析】【解答】解:28.26÷ ÷3=28.26(平方米),
答:沙堆的底面积是28.26平方米.
故选:B.
【分析】根据圆锥的体积公式:V= sh可计算出圆锥的底面积,即用沙子的体积除以再除以高即可得到答案.
6.【答案】C
【解析】【解答】3.14×(20÷2)2×6=1884,×3.14×(20÷2)2×18=1884 故答案为:C。
【分析】解答此题先用圆柱的体积公式求出水的体积,然后求出圆锥的体积,找到和圆柱内水的体积相同的圆锥的体积即可解答此题。
7.【答案】B
【解析】【解答】解:设圆锥的底面半径为r , 高为h , 则扩大后的半径4r ,
原来的体积: πr2h ,
现在的体积: π(4r)2h= πr2h ,
体积扩大: πr2h÷ πr2h=16倍;
【分析】圆锥体的体积= ×底面积×高,设圆锥的底面半径为r,高为h,则扩大后的半径为4r,分别求出变化前后的体积,即可求得体积扩大的倍数。
故选:B
二、判断题
8.【答案】错误
【解析】【解答】圆锥的高=9.42×3÷(3.14×32) 故答案为:错误。 【分析】根据圆锥的体积公式可知,圆锥的高=体积×3÷底面积,据此结合题意分析即可。
9.【答案】正确
【解析】【解答】由题意得:圆柱的底面积×高×3=圆锥的底面积×高×,已知它们的底面积相等,所以,圆柱的高×3=圆锥的高×,即圆锥的高是圆柱高的9倍。 故答案为:正确。 【分析】由题意可得等量关系:圆柱的底面积×高×3=圆锥的底面积×高×,已知它们的底面积相等,那么由此可求得圆锥的高的是圆柱高的几倍,然后再进行判断即可。
10.【答案】错误
【解析】【解答】解:圆锥的体积等于圆柱体积的三分之一是错误的,只有在圆锥、圆柱等底、等高的情况下,圆锥的体积等于圆柱体积的三分之一. 故答案为:错误. 【分析】等底等高的圆锥体积是圆柱体积的三分之一,在没有等底等高一条件,圆锥的体积可能小于圆柱的体积,也可能等于圆柱的体积或大小圆柱的体积.圆柱和圆锥只有体积、底面积、高,这三个条件中,其中两个相等,才能比较第三个.
11.【答案】错误
【解析】【解答】圆锥只有一条高。 故答案为:错误。
【分析】圆锥只有一条高,圆锥的高是圆锥的顶点到底面圆心的距离,两点确定一条线段,因此圆锥只有一条高。
12.【答案】正确
【解析】【解答】解:根据圆锥的特征可知:从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形.原题说法正确. 故答案为:正确
【分析】从圆锥的顶点向底面垂直切割,会得到两个切面,这两个切面都是三角形且是等腰三角形.
三、填空题
13.【答案】3
【解析】【解答】一个圆锥和一个圆柱的体积相等,底面积也相等.这个圆锥的高是圆柱的高的3倍. 故答案为:3. 【分析】根据圆柱和圆锥的体积公式,圆柱的体积=底面积×高,圆锥的体积=底面积×高,当体积和底面积相等时,圆锥的高是圆柱的3倍.
14.【答案】
【解析】【解答】设圆柱和圆锥的底面积都是S,高都是h,则 圆柱体积:V=Sh; 圆锥体积:V=Sh; (Sh-Sh)÷Sh =Sh÷Sh = 故答案为:.
【分析】根据题意可知,等底等高的圆柱体积是圆锥体积的3倍,据此设出圆柱和圆锥的底面积都是S,高都是h,分别求出圆锥和圆柱的体积,然后用(圆柱的体积-圆锥的体积)÷圆柱的体积,据此列式解答.
15.【答案】3:4
【解析】【解答】假设圆柱的底面半径是1,那么圆锥的底面半径是2, V柱:V锥=(π×12h):(π×22h) ????????? =πh:πh ????????? =1: ????????? =3:4 故答案为:3:4. 【分析】由“底面半径之比是1:2”可知,假设圆柱的底面半径是1,那么圆锥的底面半径是2,可用体积的字母公式列成比来解答.
16.【答案】18
【解析】【解答】6×3=18(厘米) 故答案为:18.
【分析】一个圆柱体和一个圆锥体的底面积和体积分别相等,则圆锥的高是圆柱高的3倍,据此解答.
17.【答案】339.12
【解析】【解答】×3.14×62×9=339.12(立方厘米) 【分析】解答此题要运用圆锥的体积公式,即圆锥体积=底面积×高,然后代入数据计算即可。
四、计算题
18.【答案】解答:282.6×3÷(3.14×62)=7.5(厘米)
答:圆锥零件的高是7.5厘米。
【解析】【分析】根据题意,铁块的体积等于熔铸成的圆锥体的体积,然后再用铁块的体积乘3除以圆锥的底面积,列式解答即可得到答案。
五、解答题
19.【答案】解:方法一:
①把圆锥的底面放平;
②将一块平板水平地放在圆锥的顶点上面;
③竖直地量出乎板和底面之间的距离。所测量出的距离就是圆锥的高。
方法二:直接用直尺测量(误差大)。
方法三:仿照方法一,把圆锥的底面朝上,保持平衡,底面圆所指的刻度即为圆锥的高。
【解析】【分析】解答此题首先要明确圆锥顶点到底圆中心的距离叫高,不能用刻度尺直接测量,也可以利用一个三角板和一把刻度尺根据矩形对边平行且相等间接测量。
20.【答案】(1)解:
(2)解:50.24立方厘米
【解析】【解答】已知底面半径是4厘米,所以这个直角三角形的底是4厘米,高是3厘米,绕3厘米直角边旋转的,体积是×3.14×42=50.24(立方厘米)
【分析】根据旋转后得到的圆锥的底面半径是4厘米,高是3厘米可知,直角三角形的一条直角边是4厘米,另一条是3厘米,绕着3厘米的直角边旋转即可,根据数据进行作图即可;根据圆锥的体积公式V=sh进行计算即可得到答案。
六、应用题
21.【答案】;?( 吨) 答:这堆沙重37.68吨。?
【解析】【解答】 ;所以这堆沙重 吨。 【分析】先求沙堆的体积。
22.【答案】解:该圆锥沙堆的体积为: S·h = ×9.42×0.9 =2.826(立方米) 沙坑的底面积为:S=ab=4.5×2=9 (平方米) 则铺成的沙的高度为:2.826÷9=0.314 (米) 答:可以铺0.314米.
【解析】【分析】根据题意,已知圆锥的底面积和高,求圆锥的体积,用公式:V=Sh,然后求出沙坑的底面积,用长×宽=沙坑的底面积,然后用圆锥沙堆的体积÷沙坑的底面积=铺沙的厚度,据此解答.
