数学人教B版选修2-2 1.1.1 函数的平均变化率 课件(21张)
文档属性
| 名称 | 数学人教B版选修2-2 1.1.1 函数的平均变化率 课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 321.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-07 10:48:20 | ||
图片预览






文档简介
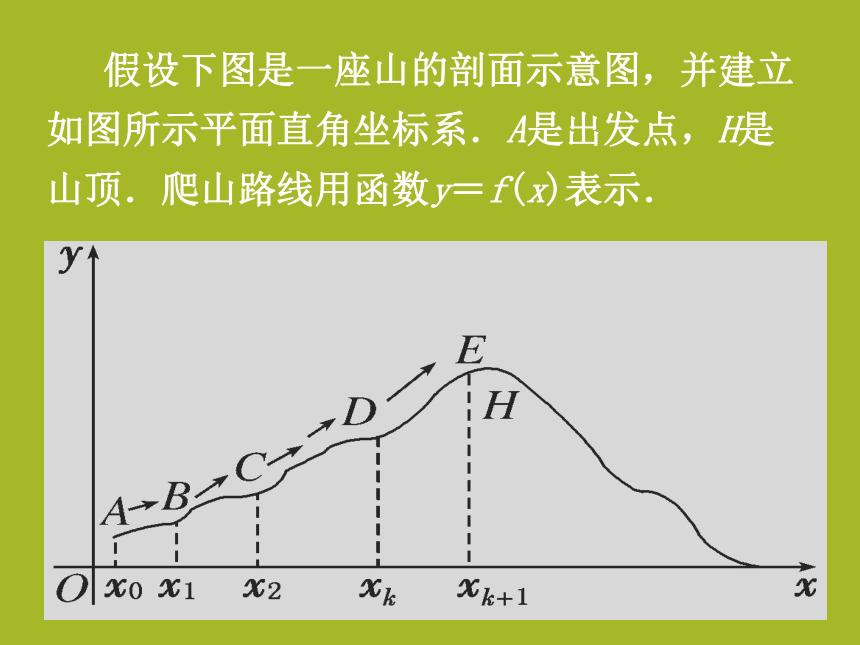
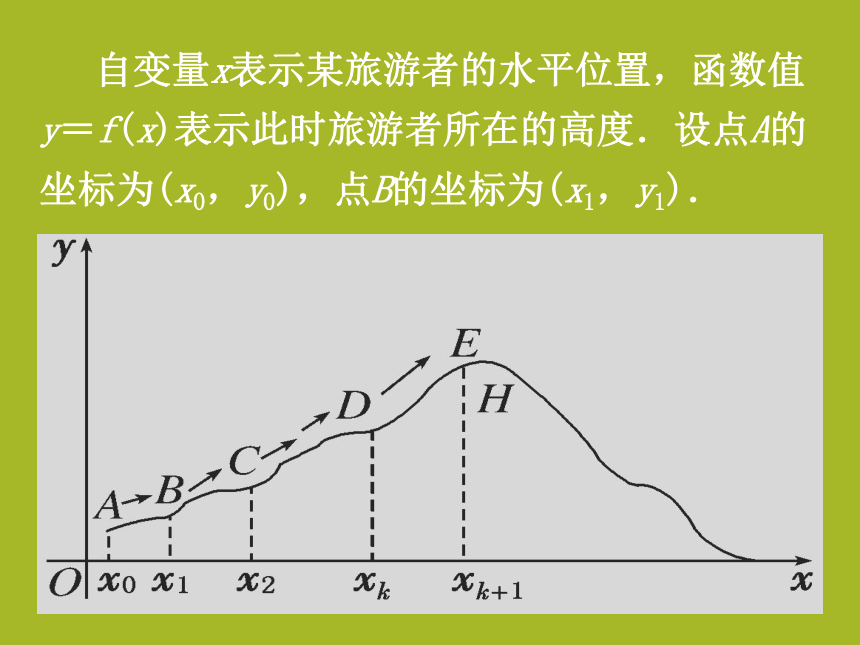
课件21张PPT。第一章 导数及其应用1.1.1 函数的平均变化率 假设下图是一座山的剖面示意图,并建立如图所示平面直角坐标系.A是出发点,H是山顶.爬山路线用函数y=f(x)表示. 自变量x表示某旅游者的水平位置,函数值y=f(x)表示此时旅游者所在的高度.设点A的坐标为(x0,y0),点B的坐标为(x1,y1). 问题1:若旅游者从点A爬到点B,且这段山路是平直的,自变量x和函数值y的改变量分别是多少?
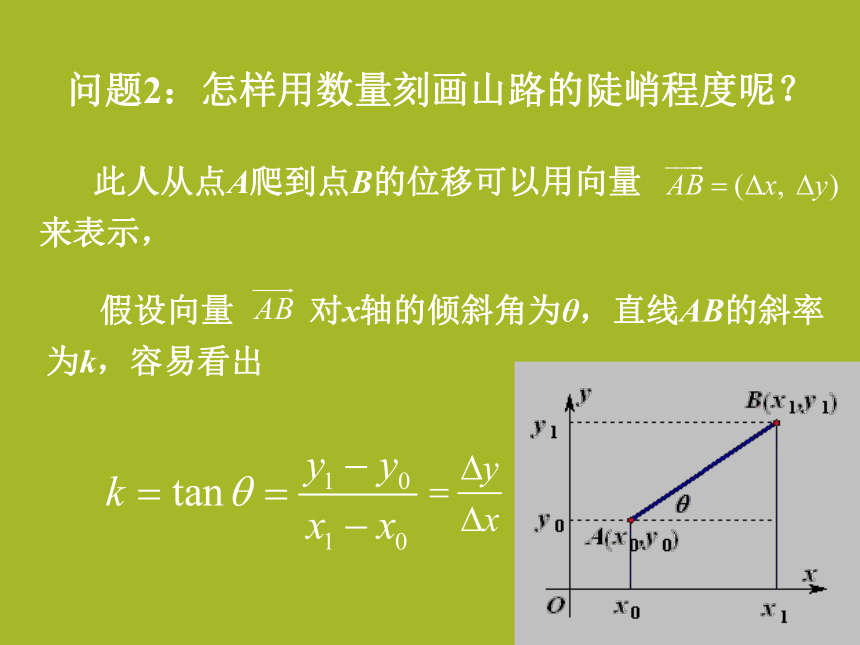
自变量x的改变量为x1-x0,记作Δx,函数值的改变量为y1-y0,记作Δy.问题2:怎样用数量刻画山路的陡峭程度呢? 此人从点A爬到点B的位移可以用向量 来表示, 假设向量 对x轴的倾斜角为θ,直线AB的斜率为k,容易看出问题3: 能否刻画山路陡峭程度呢 ? 因表示A、B两点所在直线的斜率k,显然,“线段”所在直线的斜率的绝对值越大,山坡越陡.这就是说,竖直位移与水平位移之比 的绝对值越大,山坡越陡,反之,山坡越缓. 现在摆在我们面前的问题是:山路是弯曲的,怎样用数量刻画弯曲山路的陡峭程度呢? 一个很自然的想法是将弯曲的山路分成许多小段,每一小段的山坡可视为平直的。例如,山坡DE可近似的看作线段DE,再用对平直山坡AB分析的方法,得到此段山路的陡峭程度可以用比值近似地刻画。 注意:各小段的 是不尽相同的。但不管是哪一小段山坡,高度的平均变化都可以用起点、终点的纵坐标之差与横坐标之差的比值
来度量。由此我们引出函数平均变化率的概念。 平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点,记△x=x1-x0,△y=y1-y0=f(x1)-f(x0)=f(x0+△x)-f(x0). 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。概念理解 (1)x0,x1是定义域内不同的两点,
因此Δx≠0,但Δx可正也可负;
而Δy=f(x1)-f(x0)为相应Δx=x1-x0的改变量,
因此Δy的值可正可负,也可为零.
所以,平均变化率可正可负,也可为零.(2)函数f(x)在点x0处的平均变化率与自变量的增量Δx
有关,与x0也有关.(3)函数平均变化率的几何意义:函数图象上两点
连线的斜率.求函数平均变化率的步骤
求函数y=f(x)在x0附近的平均变化率
(1)确定自变量改变量?x
(2)求函数改变量?y
(3)求平均变化率例1.求函数y=x2在区间[x0,x0+△x] (或 [x0+△x,x0])的平均变化率。解:函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率为 探究一:计算函数f(x)=x2在区间[1,1+Δx](Δx>0)的平均变化率,其中Δx的值为:
(1)2;(2)1;(3)0.1;(4)0.01.
思考:当Δx越来越小时,函数f(x)在区间[1,1+Δx]上的平均变化率有怎样的变化趋势?
探究二:求函数f(x)=x2在x0=1,2,3附近的平均变化率
,取Δx的值为2,哪一点附近的平均变化率最大?
思考:当x0越来越大时,函数f(x)在x0附近的平均变
化率有怎样的变化趋势? 由上式可以看出,当x0取定值时,△x取不同的值,函数的平均变化率不同,当△x取定值,x0取不同的值时,该函数的平均变化率也不一样。
例如,x0取正值,并不断增大时,该函数的平均变化率也不断地增大,曲线变得越来越陡峭。例2.求函数 在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率(x0≠0,且x0+△x≠0).解:函数 的平均变化率为 1.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为 ( )
A.0.40 B.0.41
C.0.43 D.0.44
解析:Δy=f(2+Δx)-f(2)=f(2.1)-f(2)=2.12-22=0.41.
答案:B课堂练习课堂练习2.已知函数f(x)=-x2+x的图象上的一点
A(-1, -2)及临近一点B(-1+△x, -2+△y),
则 .
小结: 1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)确定自变量改变量?x
(2)求函数改变量?y
(3)求平均变化率
自变量x的改变量为x1-x0,记作Δx,函数值的改变量为y1-y0,记作Δy.问题2:怎样用数量刻画山路的陡峭程度呢? 此人从点A爬到点B的位移可以用向量 来表示, 假设向量 对x轴的倾斜角为θ,直线AB的斜率为k,容易看出问题3: 能否刻画山路陡峭程度呢 ? 因表示A、B两点所在直线的斜率k,显然,“线段”所在直线的斜率的绝对值越大,山坡越陡.这就是说,竖直位移与水平位移之比 的绝对值越大,山坡越陡,反之,山坡越缓. 现在摆在我们面前的问题是:山路是弯曲的,怎样用数量刻画弯曲山路的陡峭程度呢? 一个很自然的想法是将弯曲的山路分成许多小段,每一小段的山坡可视为平直的。例如,山坡DE可近似的看作线段DE,再用对平直山坡AB分析的方法,得到此段山路的陡峭程度可以用比值近似地刻画。 注意:各小段的 是不尽相同的。但不管是哪一小段山坡,高度的平均变化都可以用起点、终点的纵坐标之差与横坐标之差的比值
来度量。由此我们引出函数平均变化率的概念。 平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点,记△x=x1-x0,△y=y1-y0=f(x1)-f(x0)=f(x0+△x)-f(x0). 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。概念理解 (1)x0,x1是定义域内不同的两点,
因此Δx≠0,但Δx可正也可负;
而Δy=f(x1)-f(x0)为相应Δx=x1-x0的改变量,
因此Δy的值可正可负,也可为零.
所以,平均变化率可正可负,也可为零.(2)函数f(x)在点x0处的平均变化率与自变量的增量Δx
有关,与x0也有关.(3)函数平均变化率的几何意义:函数图象上两点
连线的斜率.求函数平均变化率的步骤
求函数y=f(x)在x0附近的平均变化率
(1)确定自变量改变量?x
(2)求函数改变量?y
(3)求平均变化率例1.求函数y=x2在区间[x0,x0+△x] (或 [x0+△x,x0])的平均变化率。解:函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率为 探究一:计算函数f(x)=x2在区间[1,1+Δx](Δx>0)的平均变化率,其中Δx的值为:
(1)2;(2)1;(3)0.1;(4)0.01.
思考:当Δx越来越小时,函数f(x)在区间[1,1+Δx]上的平均变化率有怎样的变化趋势?
探究二:求函数f(x)=x2在x0=1,2,3附近的平均变化率
,取Δx的值为2,哪一点附近的平均变化率最大?
思考:当x0越来越大时,函数f(x)在x0附近的平均变
化率有怎样的变化趋势? 由上式可以看出,当x0取定值时,△x取不同的值,函数的平均变化率不同,当△x取定值,x0取不同的值时,该函数的平均变化率也不一样。
例如,x0取正值,并不断增大时,该函数的平均变化率也不断地增大,曲线变得越来越陡峭。例2.求函数 在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率(x0≠0,且x0+△x≠0).解:函数 的平均变化率为 1.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为 ( )
A.0.40 B.0.41
C.0.43 D.0.44
解析:Δy=f(2+Δx)-f(2)=f(2.1)-f(2)=2.12-22=0.41.
答案:B课堂练习课堂练习2.已知函数f(x)=-x2+x的图象上的一点
A(-1, -2)及临近一点B(-1+△x, -2+△y),
则 .
小结: 1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)确定自变量改变量?x
(2)求函数改变量?y
(3)求平均变化率
