17.1 勾股定理(3)课件
图片预览


文档简介
(共26张PPT)
人教版数学八年级下册
17.1勾股定理(3)
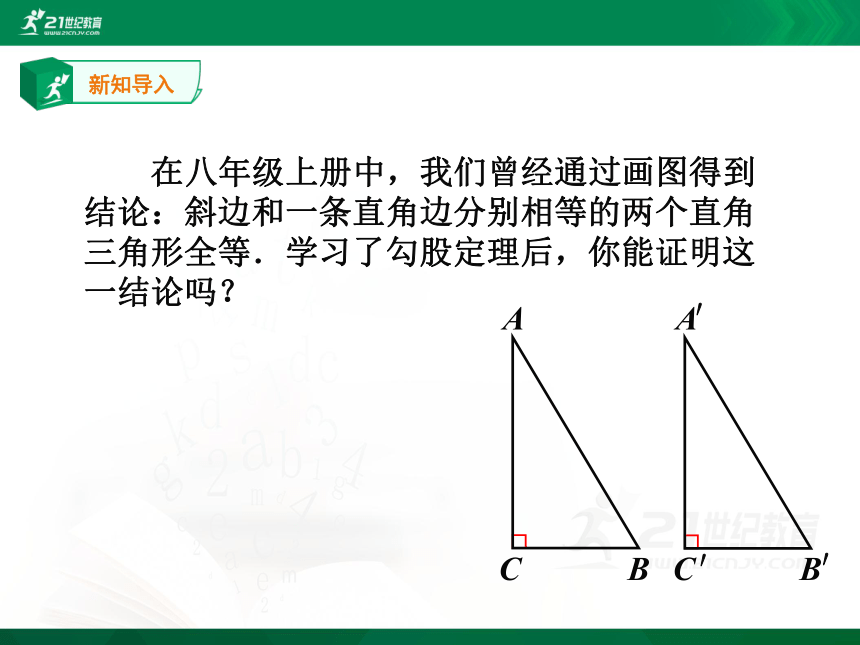
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
A
B
C
A
B
C′
′
′
新知导入
′
′
′
′
′
′
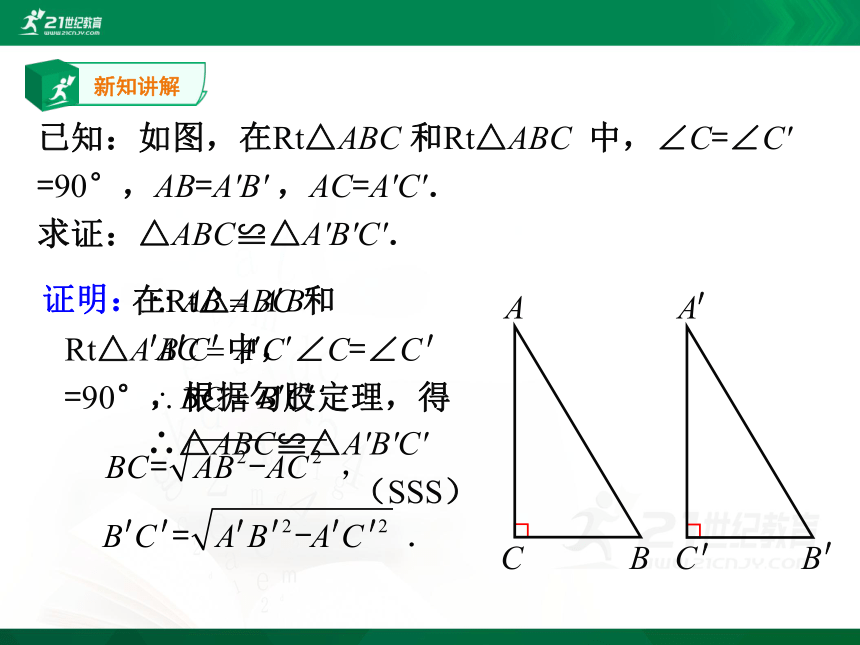
已知:如图,在Rt△ABC 和Rt△ABC 中,∠C=∠C'
=90°,AB=A'B' ,AC=A'C'.
求证:△ABC≌△A'B'C'.
在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
新知讲解
证明:
∴△ABC≌△A'B'C'
(SSS)
步骤:
l
A
B
4
0
1
2
3
C
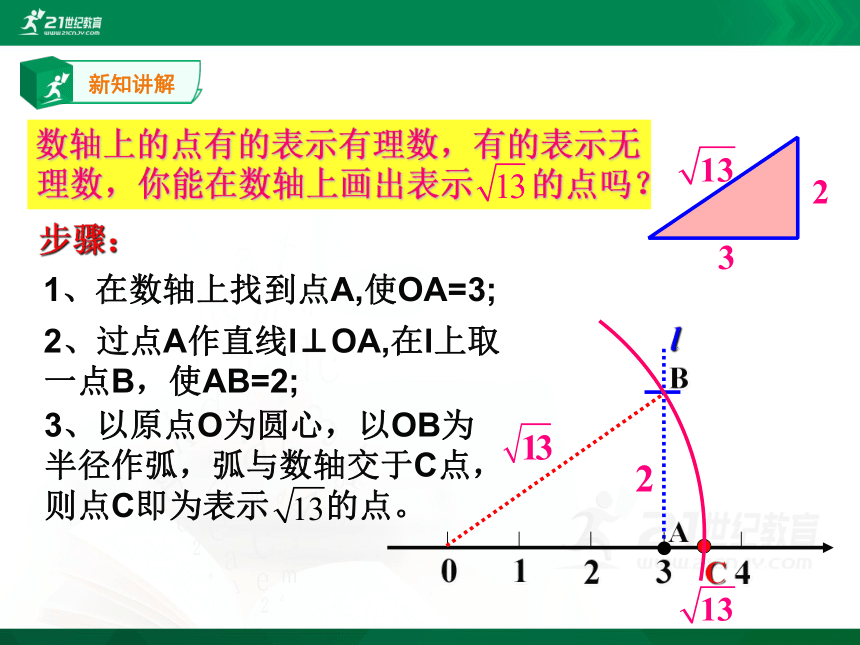
1、在数轴上找到点A,使OA=3;
2、过点A作直线l⊥OA,在l上取一点B,使AB=2;
3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
新知讲解
0
1
2
3
4
l
A
B
C
√
√
0
1
2
3
4
A
B
C
新知讲解
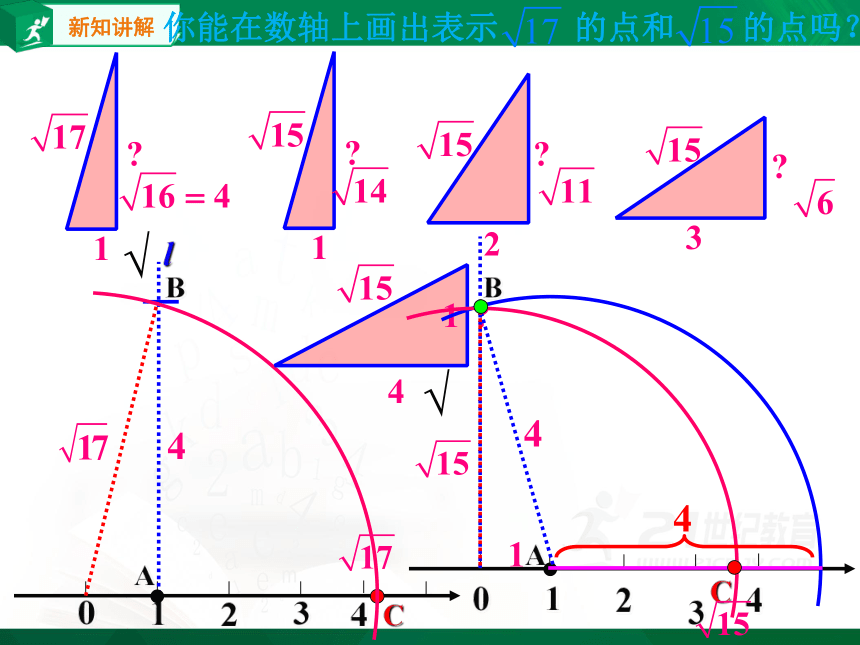
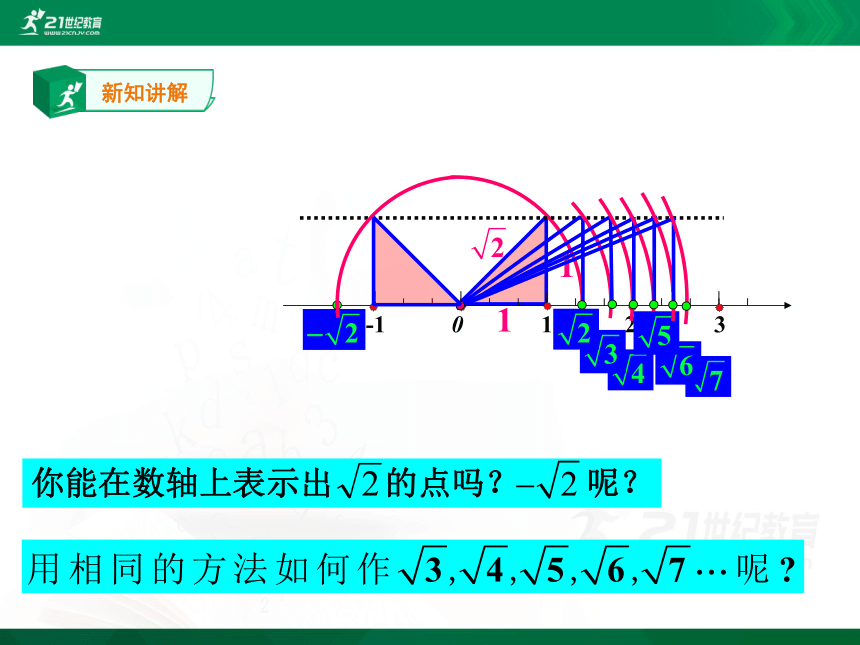
你能在数轴上画出表示 的点和 的点吗?
-1 0 1 2 3
新知讲解
你能在数轴上表示出 的点吗? 呢?
在数学中也有这样一幅美丽的“海螺型”图案。
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
数学海螺图
新知讲解
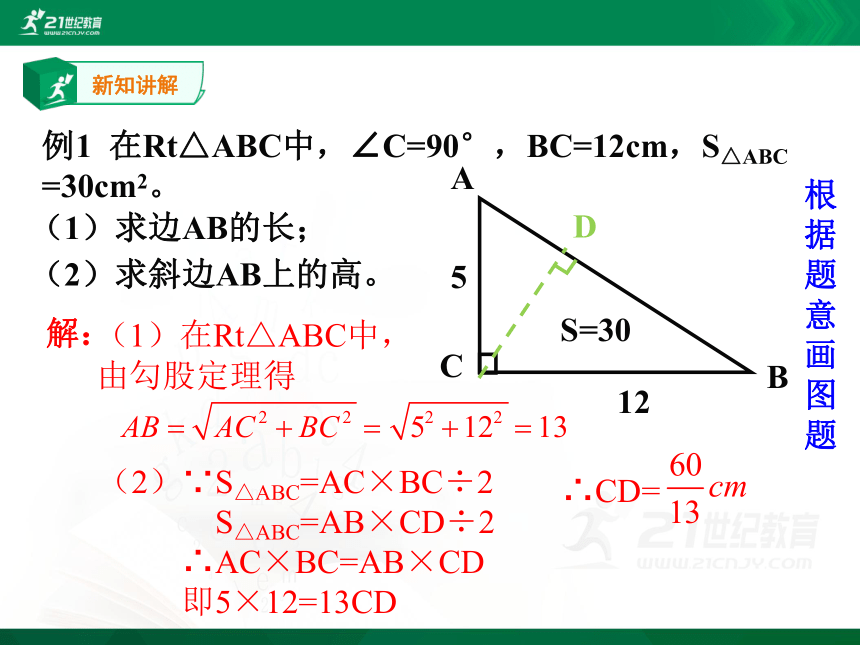
例1 在Rt△ABC中,∠C=90°,BC=12cm,S△ABC =30cm2。
A
B
C
12
S=30
5
根据题意画图题
新知讲解
(1)求边AB的长;
(2)求斜边AB上的高。
解:
(1)在Rt△ABC中,由勾股定理得
D
(2)∵S△ABC=AC×BC÷2
S△ABC=AB×CD÷2
∴AC×BC=AB×CD
即5×12=13CD
∴CD=
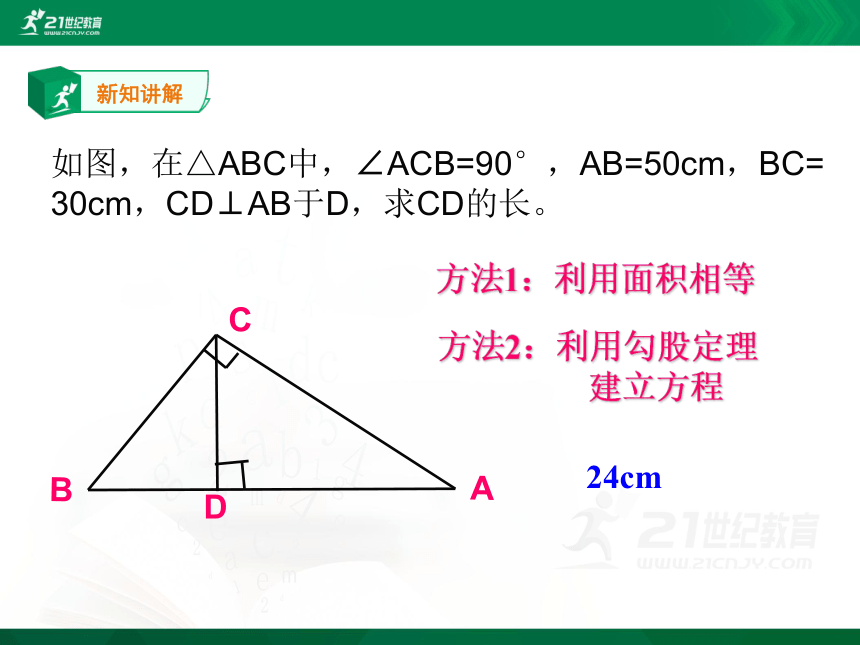
如图,在△ABC中,∠ACB=90°,AB=50cm,BC=
30cm,CD⊥AB于D,求CD的长。
A
B
C
D
方法1:利用面积相等
方法2:利用勾股定理
建立方程
新知讲解
24cm
例2 在等腰△ABC中,腰AB=10cm,底BC=16cm,求底边BC上的高AD。
A
B
C
D
新知讲解
解:
依题意AC=AB=10cm.
又∵AD⊥BC
∴BD= BC=8cm
在Rt△ABD中,由勾股定理得
在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
D
A
B
C
13
13
10
H
新知讲解
例3 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
A
B
C
15
14
13
D
方法:利用勾股定理建立方程
新知讲解
14-x
x
解:
在Rt△ABD中,
在Rt△ACD中,
设CD=x,那么BD=14-x.
解得x=5
例4 如图,有一块直角三角形纸板ABC,两直角边AC
=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且点C落到点E处,求CD的长。
拓展提高
x
x
8-x
解:
C
A
B
D
E
6
8
4
6
由折叠可知AE=AC=6,
DE=DC,DE⊥AB。
在Rt△ABC中,由勾股定理得
∴BE=AB-AE=4
在Rt△BDE中,由勾股定理得
解得x=3
设CD=x.
即CD的长为3.
如图,矩形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合,求折叠后DE和折痕EF的长.
D
A
B
C
E
F
G
拓展提高
小结:折叠问题里通常隐含了全等形,因此会产生很多相等的角和线段,要注意发掘,这些都是解题的关键。
例5 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=
30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
拓展提高
如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,且BD=AD=10,∠ADC=60° ,求△ABC的面积.
A
60°
C
B
D
拓展提高
小结:含特殊角的直角三角形也是常考查的对象。
30°所对的直角边是斜边的一半,长直角边等于短直角边的 倍;含45°的直角三角形两直角边相等,斜边等于直角边的 倍。
例6 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
拓展提高
如图,△ACB和△ECD都是等腰直角三角形,∠ACB
=∠ECD =90°,D为AB边上一点.
求证:AD2 +DB2 =DE2.
证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.
A
B
C
D
E
拓展提高
例7 如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个 写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
拓展提高
(1)本节课学习了勾股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
课堂总结
2.如图,在△ABC中,AB=15,AC= 20,BC边上的高AD=12,求BC的长。
C
A
B
D
当堂检测
1.在Rt△ABC中,∠C=90°,a=8,c=17,求△ABC的周长和△ABC的面积。
A
B
D
C
3.如图,等边△ABC,高AD=6。(1)求等边三角形的边长;(2)求△ABC的面积。
60
25
4.已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC。
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, ∠ADB = 90°
若等边三角形的边长是a呢?
当堂检测
A
B
C
D
E
F
5.如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___。
6
当堂检测
6.已知,在△ABC中,∠C=900,AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE.求CD的长度.
必做题:教材第29页习题17.1第11、12题.
选做题: 教材习题17.1第14题.
作业布置
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
人教版数学八年级下册
17.1勾股定理(3)
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
A
B
C
A
B
C′
′
′
新知导入
′
′
′
′
′
′
已知:如图,在Rt△ABC 和Rt△ABC 中,∠C=∠C'
=90°,AB=A'B' ,AC=A'C'.
求证:△ABC≌△A'B'C'.
在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
新知讲解
证明:
∴△ABC≌△A'B'C'
(SSS)
步骤:
l
A
B
4
0
1
2
3
C
1、在数轴上找到点A,使OA=3;
2、过点A作直线l⊥OA,在l上取一点B,使AB=2;
3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
新知讲解
0
1
2
3
4
l
A
B
C
√
√
0
1
2
3
4
A
B
C
新知讲解
你能在数轴上画出表示 的点和 的点吗?
-1 0 1 2 3
新知讲解
你能在数轴上表示出 的点吗? 呢?
在数学中也有这样一幅美丽的“海螺型”图案。
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
数学海螺图
新知讲解
例1 在Rt△ABC中,∠C=90°,BC=12cm,S△ABC =30cm2。
A
B
C
12
S=30
5
根据题意画图题
新知讲解
(1)求边AB的长;
(2)求斜边AB上的高。
解:
(1)在Rt△ABC中,由勾股定理得
D
(2)∵S△ABC=AC×BC÷2
S△ABC=AB×CD÷2
∴AC×BC=AB×CD
即5×12=13CD
∴CD=
如图,在△ABC中,∠ACB=90°,AB=50cm,BC=
30cm,CD⊥AB于D,求CD的长。
A
B
C
D
方法1:利用面积相等
方法2:利用勾股定理
建立方程
新知讲解
24cm
例2 在等腰△ABC中,腰AB=10cm,底BC=16cm,求底边BC上的高AD。
A
B
C
D
新知讲解
解:
依题意AC=AB=10cm.
又∵AD⊥BC
∴BD= BC=8cm
在Rt△ABD中,由勾股定理得
在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
D
A
B
C
13
13
10
H
新知讲解
例3 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
A
B
C
15
14
13
D
方法:利用勾股定理建立方程
新知讲解
14-x
x
解:
在Rt△ABD中,
在Rt△ACD中,
设CD=x,那么BD=14-x.
解得x=5
例4 如图,有一块直角三角形纸板ABC,两直角边AC
=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且点C落到点E处,求CD的长。
拓展提高
x
x
8-x
解:
C
A
B
D
E
6
8
4
6
由折叠可知AE=AC=6,
DE=DC,DE⊥AB。
在Rt△ABC中,由勾股定理得
∴BE=AB-AE=4
在Rt△BDE中,由勾股定理得
解得x=3
设CD=x.
即CD的长为3.
如图,矩形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合,求折叠后DE和折痕EF的长.
D
A
B
C
E
F
G
拓展提高
小结:折叠问题里通常隐含了全等形,因此会产生很多相等的角和线段,要注意发掘,这些都是解题的关键。
例5 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=
30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
拓展提高
如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,且BD=AD=10,∠ADC=60° ,求△ABC的面积.
A
60°
C
B
D
拓展提高
小结:含特殊角的直角三角形也是常考查的对象。
30°所对的直角边是斜边的一半,长直角边等于短直角边的 倍;含45°的直角三角形两直角边相等,斜边等于直角边的 倍。
例6 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
拓展提高
如图,△ACB和△ECD都是等腰直角三角形,∠ACB
=∠ECD =90°,D为AB边上一点.
求证:AD2 +DB2 =DE2.
证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.
A
B
C
D
E
拓展提高
例7 如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个 写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
拓展提高
(1)本节课学习了勾股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
课堂总结
2.如图,在△ABC中,AB=15,AC= 20,BC边上的高AD=12,求BC的长。
C
A
B
D
当堂检测
1.在Rt△ABC中,∠C=90°,a=8,c=17,求△ABC的周长和△ABC的面积。
A
B
D
C
3.如图,等边△ABC,高AD=6。(1)求等边三角形的边长;(2)求△ABC的面积。
60
25
4.已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC。
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, ∠ADB = 90°
若等边三角形的边长是a呢?
当堂检测
A
B
C
D
E
F
5.如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___。
6
当堂检测
6.已知,在△ABC中,∠C=900,AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE.求CD的长度.
必做题:教材第29页习题17.1第11、12题.
选做题: 教材习题17.1第14题.
作业布置
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
