人教版高中数学必修二3.2.2直线的两点式方程28张PPT
文档属性
| 名称 | 人教版高中数学必修二3.2.2直线的两点式方程28张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-10 15:44:27 | ||
图片预览








文档简介
课件28张PPT。3.2.2直线的两点
式方程复习引入1. 直线的点斜式方程及其注意事项; 复习引入1. 直线的点斜式方程及其注意事项; 2. 直线的斜截式方程及其注意事项; 复习引入1. 直线的点斜式方程及其注意事项; 2. 直线的斜截式方程及其注意事项; 3. 若l1: y=k1x+b1, l2 :y=k2x+b2,
则l1//l2与l1⊥l2应满足怎样的关系?讲授新课 探究1:已知两点P1(x1, y1),P2(x2, y2)
(其中x1≠x2,y1≠y2),如何求出通过这两
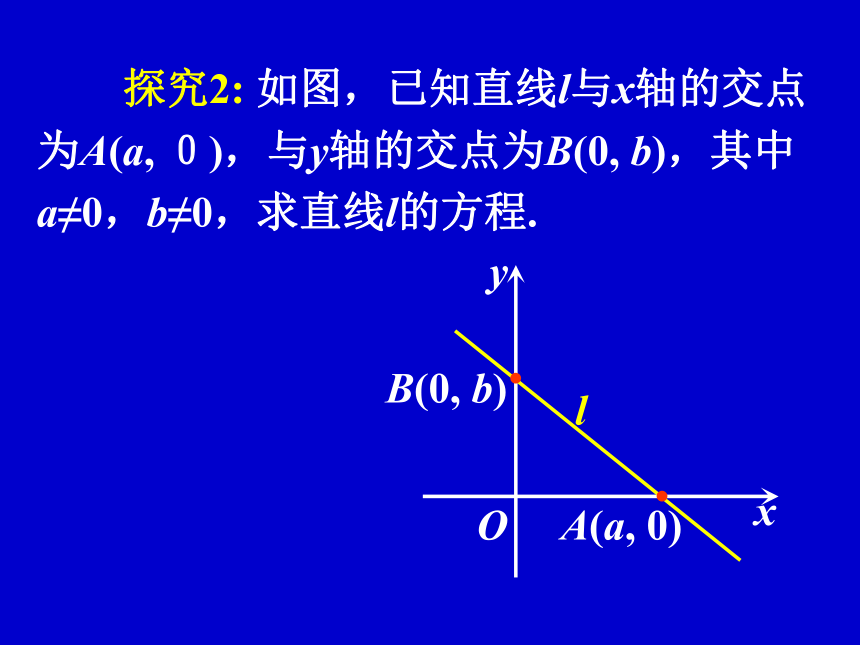
个点的直线方程呢? 探究2: 如图,已知直线l与x轴的交点
为A(a, 0),与y轴的交点为B(0, b),其中
a≠0,b≠0,求直线l的方程.lxyA(a, 0)B(0, b)O研读教材P.95-P.96:1. 直线的两点式方程是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
3. 直线的截距式方程是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
3. 直线的截距式方程是什么?
4. 直线的截距式方程适用范围是什么?点斜式方程:3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在)3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在) y=kx+b [已知斜率k存在
及截距 b(与y轴交点(0, b)]3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在) y=kx+b [已知斜率k存在
及截距 b(与y轴交点(0, b)][已知两定点(不适合与x轴
或y轴垂直的直线)]3. 两点式方程:2. 斜截式方程:直线方程模块4. 截距式方程:5. 一般式方程:直线方程模块4. 截距式方程:[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:直线方程模块4. 截距式方程: Ax+By+C=0
(A、B不同时为0)[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:直线方程模块4. 截距式方程: Ax+By+C=0
(A、B不同时为0)[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:特别的,l1:y=k1x+b1,l2:y=k2x+b2,
则 l1 //l2 ? k1=k2,且b1≠b2;
l1⊥ l2?k1·k2 =-1. 直线方程模块例1.求过下列两点的直线的两点式方程 (1) P1(2, 1),P2(0, -3); (2) A(0, 5),B(5, 0).例2.根据下列条件求直线的方程: (1)在x轴上的截距是2,在y轴上的截距为3; (2)在x轴上的截距是-5,与y轴的交点为
(0, 6).例3.根据下列条件, 求直线的方程: (1)过点(0, 5),且在两坐标轴上的截距之
和为2. (2)过点(5, 0),且在两坐标轴上的截距之
差为2.探究 线段P1P2中P1(x1, y1), P2(x2, y2), 求线段P1P2的中点P的坐标x yP2(x2, y2)P1(x1, y1)O拓展1: 过P(4, -3)且在坐标轴上截距相等
的直线有( )
A. 1条 B. 2条 C. 3条 D. 4条 思维拓展拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABO Cx拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABMO Cx拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABMO CxE课堂小结1. 两点式、截距式、中点坐标.
2. 到目前为止,我们所学过的直线方程
的表达形式有多少种?它们之间有什
么关系?
3. 要求一条直线的方程,必须知道多少
个条件?课后作业1. 阅读教材P.95到P.96;
2. 《课后限时检测》十九.
式方程复习引入1. 直线的点斜式方程及其注意事项; 复习引入1. 直线的点斜式方程及其注意事项; 2. 直线的斜截式方程及其注意事项; 复习引入1. 直线的点斜式方程及其注意事项; 2. 直线的斜截式方程及其注意事项; 3. 若l1: y=k1x+b1, l2 :y=k2x+b2,
则l1//l2与l1⊥l2应满足怎样的关系?讲授新课 探究1:已知两点P1(x1, y1),P2(x2, y2)
(其中x1≠x2,y1≠y2),如何求出通过这两
个点的直线方程呢? 探究2: 如图,已知直线l与x轴的交点
为A(a, 0),与y轴的交点为B(0, b),其中
a≠0,b≠0,求直线l的方程.lxyA(a, 0)B(0, b)O研读教材P.95-P.96:1. 直线的两点式方程是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
3. 直线的截距式方程是什么?
研读教材P.95-P.96:1. 直线的两点式方程是什么?
2. 直线的两点式方程适用范围是什么?
3. 直线的截距式方程是什么?
4. 直线的截距式方程适用范围是什么?点斜式方程:3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在)3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在) y=kx+b [已知斜率k存在
及截距 b(与y轴交点(0, b)]3. 两点式方程:2. 斜截式方程:直线方程模块点斜式方程: y-y0=k(x-x0) (已知定点
(x0, y0)及斜率k存在) y=kx+b [已知斜率k存在
及截距 b(与y轴交点(0, b)][已知两定点(不适合与x轴
或y轴垂直的直线)]3. 两点式方程:2. 斜截式方程:直线方程模块4. 截距式方程:5. 一般式方程:直线方程模块4. 截距式方程:[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:直线方程模块4. 截距式方程: Ax+By+C=0
(A、B不同时为0)[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:直线方程模块4. 截距式方程: Ax+By+C=0
(A、B不同时为0)[已知截距a(与x轴交点(a,0))及截距b(与y轴
交点(0, b))不适合过原点的直线]5. 一般式方程:特别的,l1:y=k1x+b1,l2:y=k2x+b2,
则 l1 //l2 ? k1=k2,且b1≠b2;
l1⊥ l2?k1·k2 =-1. 直线方程模块例1.求过下列两点的直线的两点式方程 (1) P1(2, 1),P2(0, -3); (2) A(0, 5),B(5, 0).例2.根据下列条件求直线的方程: (1)在x轴上的截距是2,在y轴上的截距为3; (2)在x轴上的截距是-5,与y轴的交点为
(0, 6).例3.根据下列条件, 求直线的方程: (1)过点(0, 5),且在两坐标轴上的截距之
和为2. (2)过点(5, 0),且在两坐标轴上的截距之
差为2.探究 线段P1P2中P1(x1, y1), P2(x2, y2), 求线段P1P2的中点P的坐标x yP2(x2, y2)P1(x1, y1)O拓展1: 过P(4, -3)且在坐标轴上截距相等
的直线有( )
A. 1条 B. 2条 C. 3条 D. 4条 思维拓展拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABO Cx拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABMO Cx拓展2:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)BC边所在直线的方程;
(2)BC边上中线AM所在直线的方程;
(3)高AE所在直线的方程. 思维拓展 y ABMO CxE课堂小结1. 两点式、截距式、中点坐标.
2. 到目前为止,我们所学过的直线方程
的表达形式有多少种?它们之间有什
么关系?
3. 要求一条直线的方程,必须知道多少
个条件?课后作业1. 阅读教材P.95到P.96;
2. 《课后限时检测》十九.
