数学人教A版选修2-1 1.3.1 且(and) 课件(29张)
文档属性
| 名称 | 数学人教A版选修2-1 1.3.1 且(and) 课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-11 17:27:20 | ||
图片预览







文档简介
课件29张PPT。1.3简单的逻辑联结词问题:判断下面的语句是否是命题?(1)12>5.
(2)3是12的约数.
(3)3是12的约数吗?
(4)0.4是整数.
(5)x>5.(1)(2)(4)是命题观察下列命题:
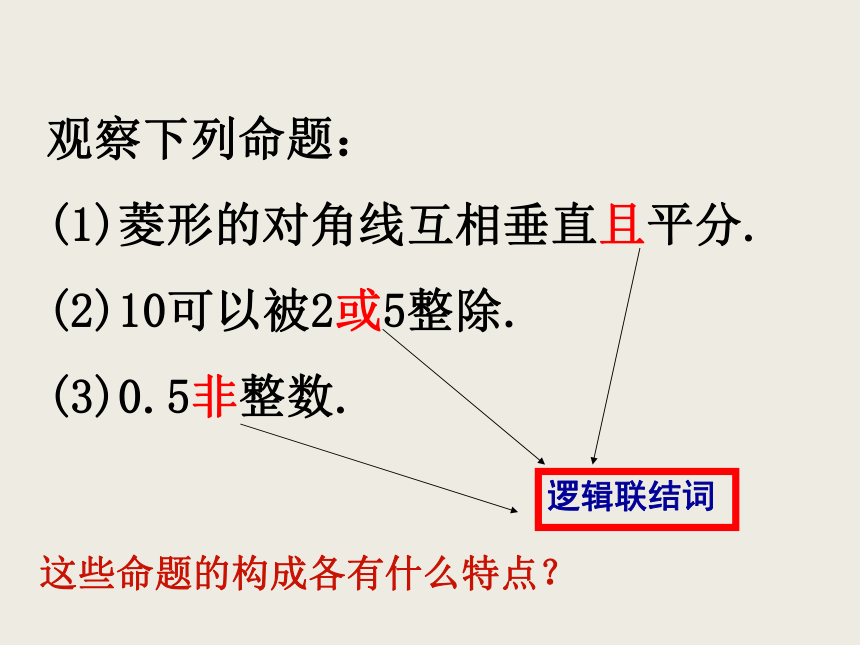
(1)菱形的对角线互相垂直且平分.
(2)10可以被2或5整除.
(3)0.5非整数.这些命题的构成各有什么特点?思考1下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除.例如:
(1)菱形的对角线互相垂直。
(2)菱形的对角线互相平分。
(3)菱形的对角线互相垂直且平分。pq 一般地,用逻辑联结词”且”把命题p和命题q联结起来.就得到一个新命题,记作
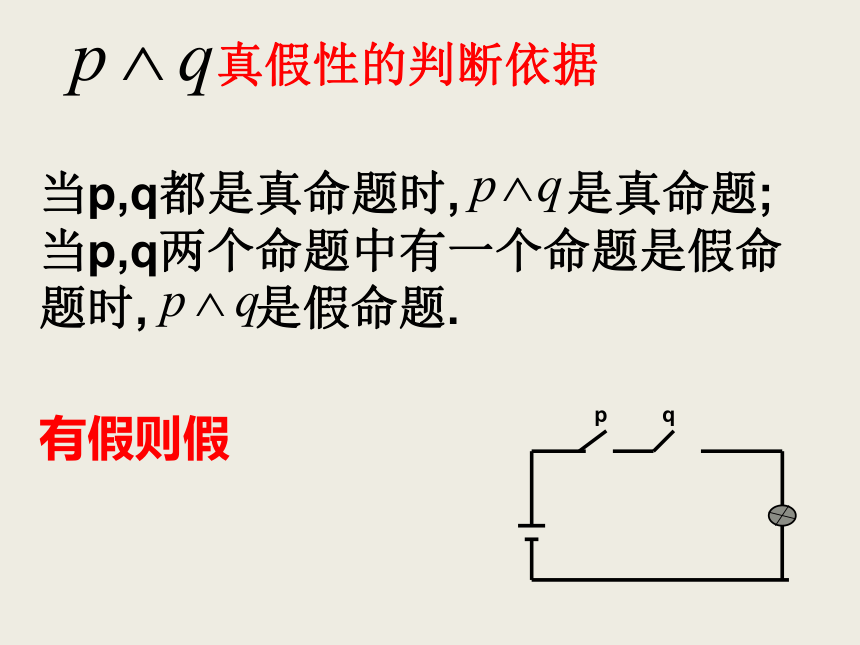
读作”p且q”.有假则假 真假性的判断依据 当p,q都是真命题时, 是真命题;当p,q两个命题中有一个命题是假命题时, 是假命题.例1:将下列命题用”且”联结成新命题,并判断它们的真假:
(1)P:平行四边形的对角线互相平分,
q:平行四边形的对角线相等.
(2) p:35是15的倍数,
q:35是7的倍数。解: p ∧q : 平行四边形的对角线互相平分且相等.解: p∧q : 35是15的倍数且是7的倍数.假命题假命题例2 用逻辑联结词“且”改写下列命题,并判断它们的真假:
(1) 1 是奇数, 是素数;
(2)2 3 都是素数。既又和既又和 解:1 是奇数且 1 是素数 解:2 是素数且 3 是素数在能用“且”改写成p∧q形式的数学命题中,通常有
“······ ······”、“······与······”、“ ······, ······”等词语。假命题真命题思考2
下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数. 一般地,用逻辑联结词”或”把命题p和命题q联结起来.就得到一个新命题,记作 规定:当p,q两个命题中有一个是真命题
时, 是真命题;当p,q两个命题中都是
假命题时, 是假命题.当p,q两个命题中有一个是真命题时, 是真命题;
当p,q两个命题都是假命题时, 是假命题. 真假性的判断依据有真则真例3:将下列命题用”或”联结成新命题,并判断它们的真假:
(1)P:π是无理数 ,
q:π是实数 .
(2) p:45是7的倍数,
q:45是8的倍数。解: p∨q : π是无理数 或是实数解: p∨q : 45是7的倍数或是8的倍数.真命题假命题例4
判断下列命题的真假
(1)2 2;
(2)集合A是 的子集或是
的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等.真真假如果 为真命题,那么 一定是真命题吗?反之,如果 为真命题,那么 一定是真命题吗?思考3
下列命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除. 一般地,对一个命题p全盘否定,就得到一个新命题,记作
若p是真命题,则 必是假命题;若p是假命题,则 必是真命题.读作”非p”或”p的否定”“非”命题对常见的几个正面词语的否定.≠≤不是不都是至少有
两个一个都
没有例5 写出下列命题的否定,并判断它们的真假:假真假否命题与命题的否定有什么区别?如:命题p:正方形的四条边相等 :正方形的四条边不相等P的否命题:若一个四边形不是正方形, 则它的四条边不相等。课堂练习一
1、判断下列命题的真假:
(1)12是48且是36的约数;
(2)矩形的对角线互相垂直且平分。
2、判断下列命题的真假
(1)47是7的倍数或49是7的倍数;
(2)等腰梯形的对角线互相平分或互相垂直。真假真假真假真假假1.理解逻辑联结词 “且”、“或”、“非”的含义.
它们与集合的“交”、“并”、“补” 之间有关系吗?2.判断含有逻辑联结词的命题真假的步骤.课堂小结3.体会用常用逻辑用语表述数学内容的准确性和简洁性。否命题与命题的否定有什么区别?如:命题p:正方形的四条边相等拓展训练:
已知p:关于x的不等式x2+(a-1)x+1≤0的解集为空集;q:函数f(x)=ax2+ax+1
没有零点,若p∧q为假命题,p∨q为真命题,
求实数a的取值范围.?(-1,0)∪[3,4).解:对于p:因为x2+(a-1)x+1≤0的解集为空集,
所以Δ=(a-1)2-4<0,解得-1故p真:-1对于q:f(x)=ax2+ax+1没有零点,等价于方程ax2+ax+1=0没有实数根,
①当a=0时,方程无实根符合题意;
②当a≠0时,Δ=a2-4a<0,解得0故q真:0≤a<4,q假:a<0或a≥4.
由p∧q为假命题,p∨q为真命题可知,p与q有且只有一个为真.
若p真q假,则-1综上可知,实数a的取值范围是(-1,0)∪[3,4).谢谢指导!
(2)3是12的约数.
(3)3是12的约数吗?
(4)0.4是整数.
(5)x>5.(1)(2)(4)是命题观察下列命题:
(1)菱形的对角线互相垂直且平分.
(2)10可以被2或5整除.
(3)0.5非整数.这些命题的构成各有什么特点?思考1下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除.例如:
(1)菱形的对角线互相垂直。
(2)菱形的对角线互相平分。
(3)菱形的对角线互相垂直且平分。pq 一般地,用逻辑联结词”且”把命题p和命题q联结起来.就得到一个新命题,记作
读作”p且q”.有假则假 真假性的判断依据 当p,q都是真命题时, 是真命题;当p,q两个命题中有一个命题是假命题时, 是假命题.例1:将下列命题用”且”联结成新命题,并判断它们的真假:
(1)P:平行四边形的对角线互相平分,
q:平行四边形的对角线相等.
(2) p:35是15的倍数,
q:35是7的倍数。解: p ∧q : 平行四边形的对角线互相平分且相等.解: p∧q : 35是15的倍数且是7的倍数.假命题假命题例2 用逻辑联结词“且”改写下列命题,并判断它们的真假:
(1) 1 是奇数, 是素数;
(2)2 3 都是素数。既又和既又和 解:1 是奇数且 1 是素数 解:2 是素数且 3 是素数在能用“且”改写成p∧q形式的数学命题中,通常有
“······ ······”、“······与······”、“ ······, ······”等词语。假命题真命题思考2
下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数. 一般地,用逻辑联结词”或”把命题p和命题q联结起来.就得到一个新命题,记作 规定:当p,q两个命题中有一个是真命题
时, 是真命题;当p,q两个命题中都是
假命题时, 是假命题.当p,q两个命题中有一个是真命题时, 是真命题;
当p,q两个命题都是假命题时, 是假命题. 真假性的判断依据有真则真例3:将下列命题用”或”联结成新命题,并判断它们的真假:
(1)P:π是无理数 ,
q:π是实数 .
(2) p:45是7的倍数,
q:45是8的倍数。解: p∨q : π是无理数 或是实数解: p∨q : 45是7的倍数或是8的倍数.真命题假命题例4
判断下列命题的真假
(1)2 2;
(2)集合A是 的子集或是
的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等.真真假如果 为真命题,那么 一定是真命题吗?反之,如果 为真命题,那么 一定是真命题吗?思考3
下列命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除. 一般地,对一个命题p全盘否定,就得到一个新命题,记作
若p是真命题,则 必是假命题;若p是假命题,则 必是真命题.读作”非p”或”p的否定”“非”命题对常见的几个正面词语的否定.≠≤不是不都是至少有
两个一个都
没有例5 写出下列命题的否定,并判断它们的真假:假真假否命题与命题的否定有什么区别?如:命题p:正方形的四条边相等 :正方形的四条边不相等P的否命题:若一个四边形不是正方形, 则它的四条边不相等。课堂练习一
1、判断下列命题的真假:
(1)12是48且是36的约数;
(2)矩形的对角线互相垂直且平分。
2、判断下列命题的真假
(1)47是7的倍数或49是7的倍数;
(2)等腰梯形的对角线互相平分或互相垂直。真假真假真假真假假1.理解逻辑联结词 “且”、“或”、“非”的含义.
它们与集合的“交”、“并”、“补” 之间有关系吗?2.判断含有逻辑联结词的命题真假的步骤.课堂小结3.体会用常用逻辑用语表述数学内容的准确性和简洁性。否命题与命题的否定有什么区别?如:命题p:正方形的四条边相等拓展训练:
已知p:关于x的不等式x2+(a-1)x+1≤0的解集为空集;q:函数f(x)=ax2+ax+1
没有零点,若p∧q为假命题,p∨q为真命题,
求实数a的取值范围.?(-1,0)∪[3,4).解:对于p:因为x2+(a-1)x+1≤0的解集为空集,
所以Δ=(a-1)2-4<0,解得-1
①当a=0时,方程无实根符合题意;
②当a≠0时,Δ=a2-4a<0,解得0
由p∧q为假命题,p∨q为真命题可知,p与q有且只有一个为真.
若p真q假,则-1
