江苏省18市县2019届高三上学期期中期末考试数学试题分类汇编:立体几何
文档属性
| 名称 | 江苏省18市县2019届高三上学期期中期末考试数学试题分类汇编:立体几何 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-11 17:18:41 | ||
图片预览

文档简介
江苏省18市县2019届高三上学期期中期末考试数学试题分类汇编
立体几何
一、填空题
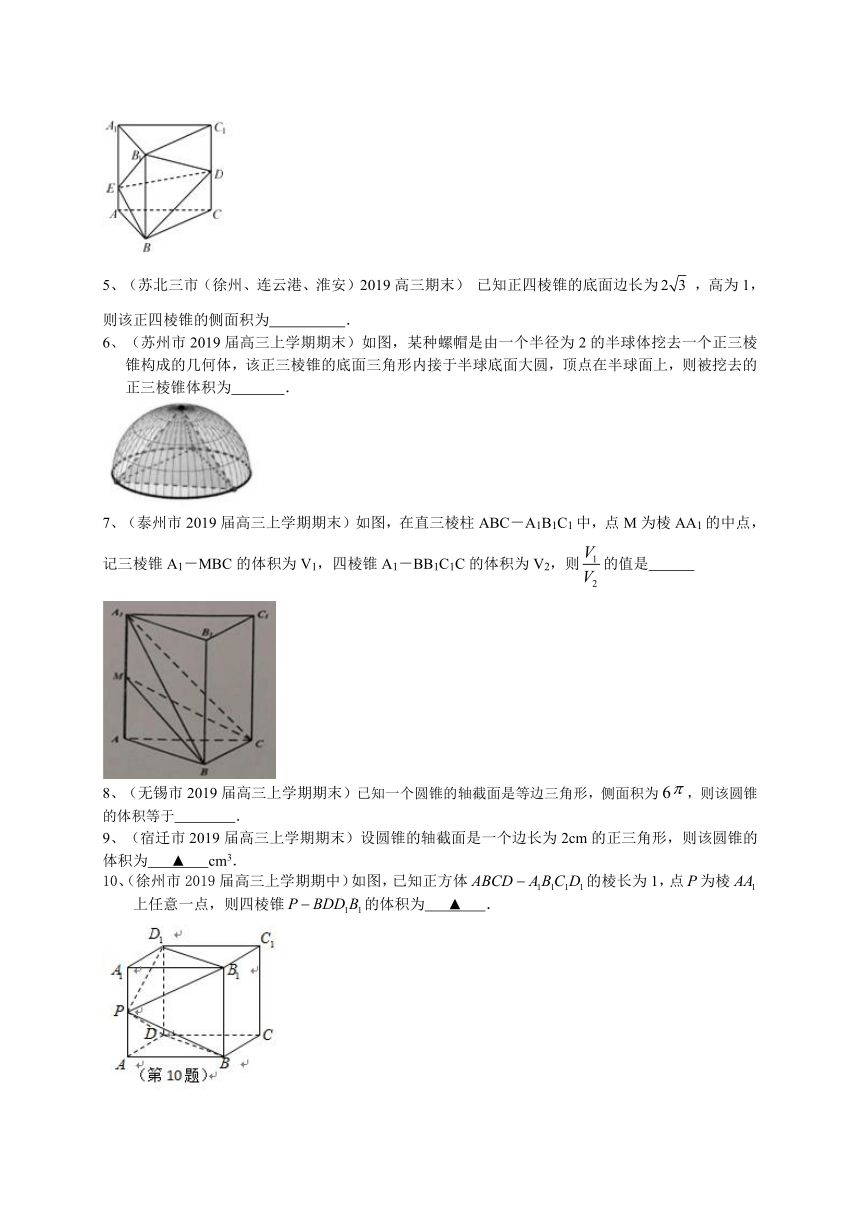
1、(常州市2019届高三上学期期末)已知圆锥,过的中点作平行于圆锥底面的截面,以截面为上底面作圆柱,圆柱的下底面落在圆锥的底面上(如图),则圆柱的体积与圆锥的体积的比值为________.
2、(南京市、盐城市2019届高三上学期期末)如图,PA⊥平面ABC,AC⊥BC,PA=4,AC=,BC=1,E,F分别为AB,PC的中点,则三棱锥B-EFC的体积为 ▲ .
3、(南通市三地(通州区、海门市、启东市)2019届高三上学期期末)
已知正三棱柱ABC-则三棱锥D-BB1C1的体积为___
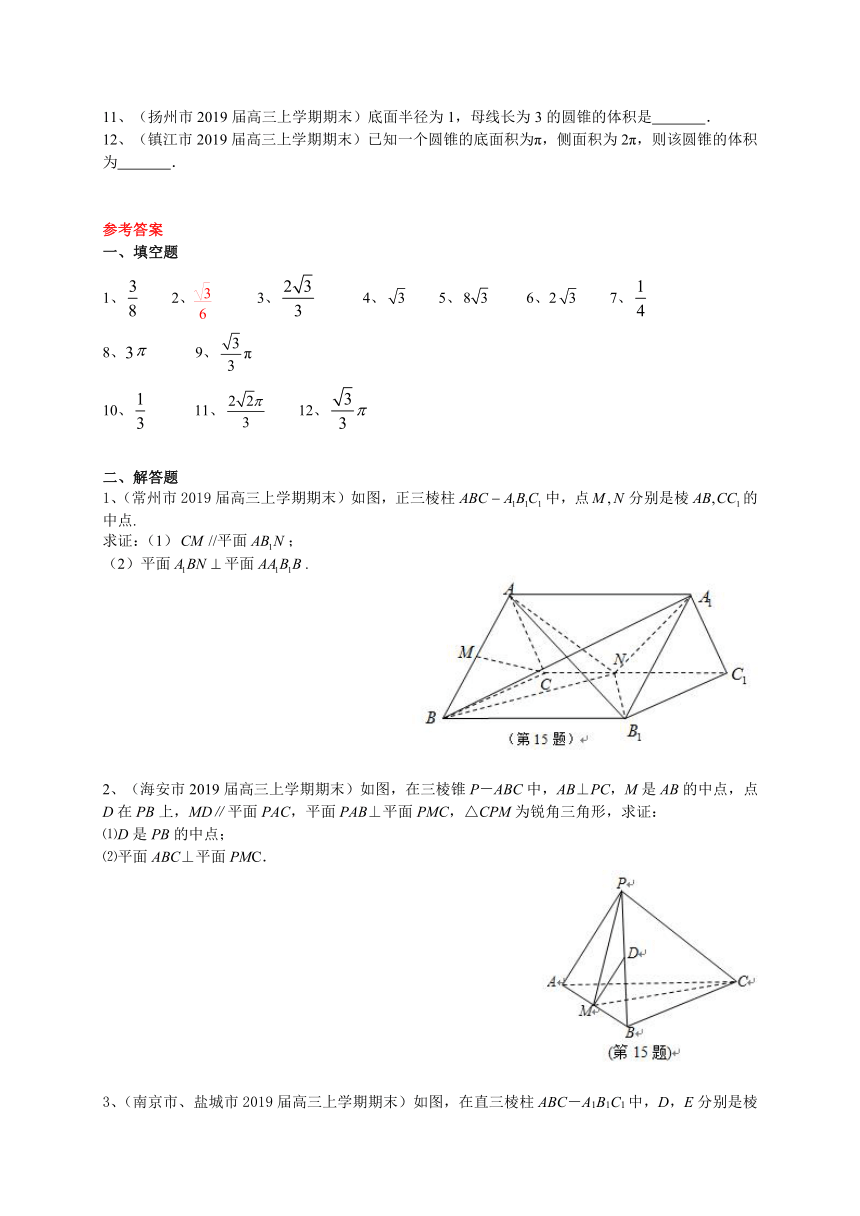
4、(如皋市2019届高三上学期期末)如图,在正三棱柱ABC-A1B1C1中,若AA1=3,AB=2,点D是棱CC1的中点,点E在棱AA1上,则三棱锥B1-EBD的体积为 ▲ .
5、(苏北三市(徐州、连云港、淮安)2019高三期末) 已知正四棱锥的底面边长为,高为1,则该正四棱锥的侧面积为 .
6、(苏州市2019届高三上学期期末)如图,某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体,该正三棱锥的底面三角形内接于半球底面大圆,顶点在半球面上,则被挖去的正三棱锥体积为 .
7、(泰州市2019届高三上学期期末)如图,在直三棱柱ABC-A1B1C1中,点M为棱AA1的中点,记三棱锥A1-MBC的体积为V1,四棱锥A1-BB1C1C的体积为V2,则的值是
8、(无锡市2019届高三上学期期末)已知一个圆锥的轴截面是等边三角形,侧面积为6,则该圆锥的体积等于 .
9、(宿迁市2019届高三上学期期末)设圆锥的轴截面是一个边长为2cm的正三角形,则该圆锥的体积为 ▲ cm3.
10、(徐州市2019届高三上学期期中)如图,已知正方体的棱长为1,点为棱上任意一点,则四棱锥的体积为 ▲ .
11、(扬州市2019届高三上学期期末)底面半径为1,母线长为3的圆锥的体积是 .
12、(镇江市2019届高三上学期期末)已知一个圆锥的底面积为π,侧面积为2π,则该圆锥的体积为 .
参考答案
一、填空题
1、 2、 3、 4、 5、 6、2 7、
8、3 9、
10、 11、 12、
二、解答题
1、(常州市2019届高三上学期期末)如图,正三棱柱中,点分别是棱的中点.
求证:(1)//平面;
(2)平面平面.
2、(海安市2019届高三上学期期末)如图,在三棱锥P-ABC中,AB⊥PC,M是AB的中点,点D在PB上,MD∥平面PAC,平面PAB⊥平面PMC,△CPM为锐角三角形,求证:
⑴D是PB的中点;
⑵平面ABC⊥平面PMC.
3、(南京市、盐城市2019届高三上学期期末)如图,在直三棱柱ABC-A1B1C1中,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为棱B1C1上的中点,且A1F⊥B1C1.
求证:(1)平面ADE⊥平面BCC1B1;
(2)A1F//平面ADE.
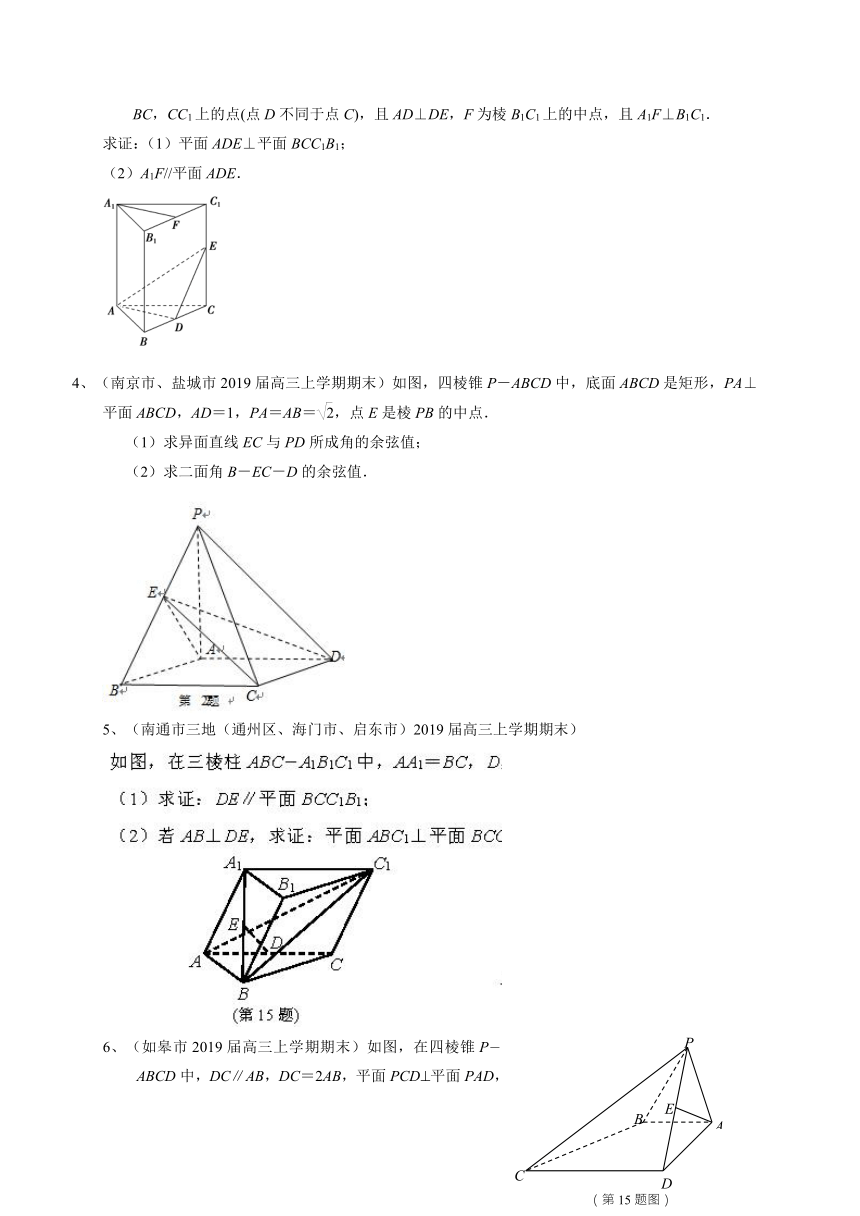
4、(南京市、盐城市2019届高三上学期期末)如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=,点E是棱PB的中点.
(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
5、(南通市三地(通州区、海门市、启东市)2019届高三上学期期末)
6、(如皋市2019届高三上学期期末)如图,在四棱锥P-ABCD中,DC∥AB,DC=2AB,平面PCD平面PAD,△PAD是正三角形,E是PD的中点.
(1)求证:AE⊥PC;
(2)求证:AE∥平面PBC.
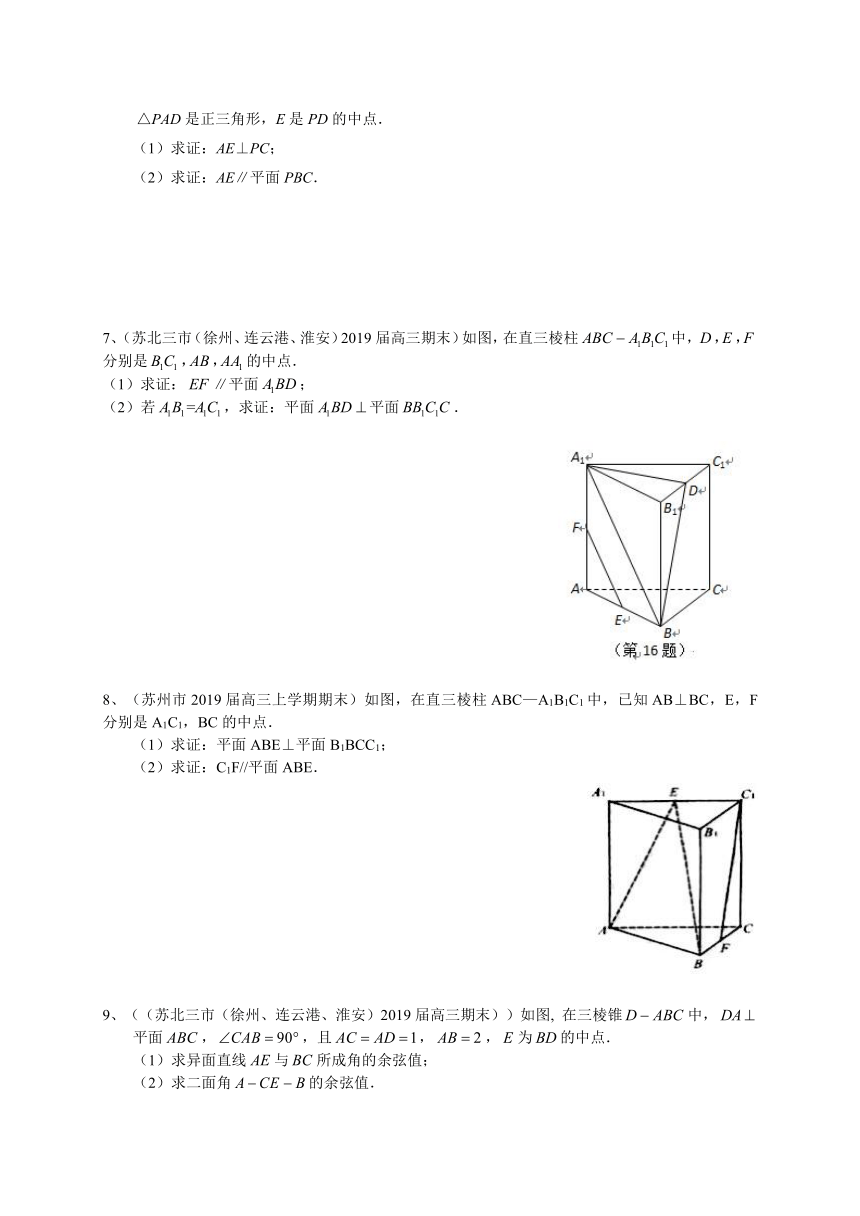
7、(苏北三市(徐州、连云港、淮安)2019届高三期末)如图,在直三棱柱中,分别是的中点.
(1)求证:∥平面;
(2)若,求证:平面平面.
8、(苏州市2019届高三上学期期末)如图,在直三棱柱ABC—A1B1C1中,已知AB⊥BC,E,F分别是A1C1,BC的中点.
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
9、((苏北三市(徐州、连云港、淮安)2019届高三期末))如图, 在三棱锥中,平面,,且,,为的中点.
(1)求异面直线与所成角的余弦值;
(2)求二面角的余弦值.
10、(泰州市2019届高三上学期期末)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点O为对角线BD的中点,点E,F分别为棱PC,PD的中点,已知PA⊥AB,PA⊥AD。
求证:(1)直线PB∥平面OEF;
(2)平面OEF⊥平面ABCD。
11、(无锡市2019届高三上学期期末)在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。
(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
12、(无锡市2019届高三上学期期中)在四棱锥P ? ABCD中,已知M,N分别是BC,PD的中点,若四边形ABCD是平行四边形,且∠BAC=90°.
(1) 求证: MN∥平面PAB;
(2) 若PA⊥平面ABCD,求证:MN⊥AC.
13、(宿迁市2019届高三上学期期末)在四棱锥中,,底面ABCD是菱形.
(1)求证:;
(2)若点是棱AD的中点,点在棱SA上,
且,求证:.
14、(徐州市2019届高三上学期期中)如图,在三棱锥中, 分别为,的中点,点在上,且底面.
(1)求证:平面;
(2)若,求证:平面平面.
15、(宿迁市2019届高三上学期期末)如图,在直三棱柱中,,,点在棱 上,且.
(1)求线段的长;
(2)求二面角的余弦值.
16、(扬州市2019届高三上学期期末)如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.
(1)求证:EF∥平面ABC;
(2)BB1⊥AC.
17、(扬州市2019届高三上学期期末)将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,又AE⊥平面ABD.
(1)若AE=,求直线DE与直线BC所成角;
(2)若二面角A—BE—D的大小为,求AE的长度.
18、(镇江市2019届高三上学期期末)如图,在四棱锥V—ABCD中,底面ABCD是矩形,VD⊥平面ABCD,过AD的平面分别与VB,VC交于点M,N.
(1)求证:BC⊥平面VCD;
(2)求证:AD∥MN.
参考答案
二、解答题
1、(1)设A1B与AB1的交点为O,连MO,NO
在正三棱柱ABC-A1B1C1中,O为AB1的中点,OM∥BB1,且OM=BB1,
依题意,有CN∥BB1,且CN=BB1,
∴ OM∥CN,且OM=CN
∴ 四边形CMON为平行四边形,
∴ CM∥ON
而CM平面AB1N,ON平面AB1N,
∴ CM∥平面AB1N。
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∴ BB1⊥CM,
又CM⊥AB,AB∩BB1=B,∴ CM⊥平面ABB1A1,
因为CM∥ON,∴ ON⊥平面ABB1A1
ON平面A1BN,
∴ 平面A1BN⊥平面ABB1A1
2、
3、证明:(1)在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC. ……………………2分
因为AD平面ABC,所以BB1⊥AD.
又因为AD⊥DE,在平面BCC1B1中,BB1与DE相交,所以AD⊥平面BCC1B1.
又因为AD平面ADE,所以平面ADE⊥平面BCC1B1. …………………6分
(2)在直三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1. …………………8分
因为A1F平面A1B1C1,所以BB1⊥A1F.
又因为A1F⊥B1C1,BB1∩B1C1=B1,所以A1F⊥平面BCC1B1. …………………10分
在(1)中已证得AD⊥平面BCC1B1,所以A1F//AD.
又因为A1F平面ADE,AD平面ADE,所以A1F//平面ADE. …………………14分
4、解:(1)因PA⊥底面ABCD,且底面ABCD为矩形,所以AB,AD,AP两两垂直,
以A为原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系,
又因PA=AB=,AD=1,
所以A(0,0,0),B(,0,0),C(,1,0),D(0,1,0),P(0,0,),………2分
因为E是棱PB的中点,所以E(,0,),
所以=(,1,-),=(0,1,-),
所以cos<,>==,
所以异面直线EC与PD所成角的余弦值为. ……………………6分
(2)由(1)得=(,1,-),=(0,1,0),=(,0,0),
设平面BEC的法向量为n1=(x1,y1,z1),所以
令x1=1,则z1=1,所以面BEC的一个法向量为n1=(1,0,1),
设平面DEC的法向量为n2=(x2,y2,z2),所以
令z2=,则y2=1,所以面DEC的一个法向量为n2=(0,1,),
所以cos<n1,n2>==.由图可知二面角B-EC-D为钝角,
所以二面角B-EC-D的余弦值为-. …………………………10分
5、
6、【证明】(1)因为△PAD是正三角形,点E是PD的中点,
所以AE⊥PD. …… 2分
又平面PCD⊥面PAD,平面PCD∩平面PAD=PD,AE?平面PAD.
所以AE⊥平面PCD. …… 5分
又PC?平面PCD,
所以AE⊥PC. …… 7分
(2)取PC的中点F,连结EF,
在△PCD中,E,F分别是PD,PC的中点,
所以EF∥CD且CD=2EF.
又AB∥CD,CD=2AB,
所以EF∥AB且EF=AB,
所以四边形AEFB是平行四边形,
所以AE∥BF, …… 10分
又AE平面PBC,BF平面PBC,
所以AE∥平面PBC. …… 14分
7、(1)因为分别是的中点,所以∥. ………………………3分
因为平面,平面,
所以∥平面. …………………………6分
(2)在直三棱柱中,平面,
因为平面,所以. ……8分
因为,且是的中点,
所以. ………………………………10分
因为,平面,
所以平面. ………………………12分
因为平面,
所以平面平面. …………………14分
8、
9、因为平面,,所以可以以为坐标原点,建立如图所示的空间直角坐标系.
因为,,
所以,,,,
因为点为线段的中点,
所以.
(1),,
所以,
所以异面直线与所成角的余弦值为.……………………………………5分
(2)设平面的法向量为,
因为,,
所以,,即且,取,得,,
所以是平面的一个法向量.
设平面的法向量为,
因为,,
所以,,
即且,取,得,,
所以是平面的一个法向量.
所以. ……………………………………8分
所以二面角的余弦值为. ………………………………………10分
10、(1)O为PB中点,F为PD中点,所以,PB∥FO
而PB平面OEF,FO平面OEF,
∴ PB∥平面OEF。
(2)连结AC,因为ABCD为平行四边形,
∴AC与BD交于点O,O为AC中点,又E为PC中点,
∴ PA∥OE,
因为PA⊥AB,PA⊥AD,AB∩AD=A,
∴ PA⊥平面ABCD,
∴ OE⊥平面ABCD
又OE平面OEF,
∴ 平面OEF⊥平面ABCD
11、答案:(1)四边形ABCD中,因为AB⊥AD,AB⊥BC,
所以,BC∥AD,BC在平面PAD外,
所以,BC∥平面PAD
(2)作DE⊥PA于E,
因为平面PAD⊥平面PAB,而平面PAD∩平面PAB=AB,
所以,DE⊥平面PAB,
所以,DE⊥AB,又AD⊥AB,DE∩AD=D
所以,AB⊥平面PAD,
AB在平面ABCD内
所以,平面PAD⊥平面ABCD
12、证明:(1) (证法1)取PA的中点G,连结BG,GN.
∵ 点N是PD的中点,∴ NG∥AD,且NG=AD.(2分)
∵ 点M是BC的中点,∴ BM=BC.
∵ 四边形ABCD是平行四边形,∴ BM∥AD,且BM=AD.(4分)
∴ 四边形BMNG是平行四边形.
又MN∥平面PAB,BG?平面PAB,
∴ MN∥平面PAB.(6分)
(证法2)取AD中点H,连结NH,MH.
∵ 点N是PD的中点,∴ NH∥PA.
又NH?平面PAB,PA?平面PAB,∴ NH∥平面PAB.(2分)
∵ M,H分别是BC,AD的中点,四边形ABCD是平行四边形,
∴ MH∥AB.
又MH?平面PAB,AB?平面PAB,∴ MH∥平面PAB.(4分)
又MH∩NH=H,∴ 平面MNH∥平面PAB.
∵ MN?平面PAB,∴ MN∥平面PAB.(6分)
(2) ∵ PA⊥平面ABCD,由(1)知NH∥PA,
∴ NH⊥平面ABCD,AC?平面ABCD.
∴ NH⊥AC,即AC⊥NH.(8分)
∵ ∠BAC=90°,∴ AC⊥AB.
又MH∥AB,∴ AC⊥MH.(10分)
∵ MH∩NH=H,NH?平面MNH,MH?平面MNH,
∴ AC⊥平面MNH.(12分)
而MN?平面MNH,∴ AC⊥MN,即MN⊥AC.(14分)
13、解:(1)因为,,
所以, ………………………………2分
又因为底面ABCD是菱形,得,
由SA,AC都在面SAC内,且,
所以,………………………………5分
由,得;…………7分
(2)由底面ABCD是菱形,得
所以………………9分
又因为,
所以 ,
所以…,………………………11分
因为,
所以.………………………………14分
14、1)由中位线知:DE‖AC,可证:DE‖平面SAC
(2)由SD⊥平面ABC,知SD⊥AC,又SF⊥AC,SD与SF交于点S,
所以,AC⊥平面SFD,所以,平面SAC⊥平面SFD
15、解:在直三棱柱中,由则以为基底构建如图所示的空间直角坐标系,则,
所以,
设,则,
(1)由得,
所以,
所以=.……………………………………………3分
(2)由,取的一个法向量为,
设的一个法向量,
由(1)知
又因为,
所以,取,
则,…………………6分
所以,
所以.
所以二面角的余弦值为.…………………………10分
16、证明:(1)∵三棱柱 ∴四边形,四边形均为平行四边形
∵分别是侧面,对角线的交点 ∴分别是,的中点
∴ ………………4分
∵平面,平面∴平面 ………………8分
(2)∵四边形为矩形 ∴
∵平面平面,平面,平面平面
∴平面 ………………12分
∵平面 ∴ ………………14分
17、解:∵正方形边长为2 ∴,,
又⊥平面
∴以点为原点,所在直线为轴建立空间直角坐标系.
作,垂足为
∵平面⊥平面,平面,平面平面
∴平面
∵ ∴点为的中点, …………2分
(1)∵
∴,,,,
∴ ∴
∴ ∴直线与直线所成角为; …………5分
(2)设的长度为,则
∵⊥平面 ∴平面的一个法向量为 …………6分
设平面的法向量为,又
∴ ∴,解得:,取,则
∴平面的一个法向量为 …………8分
∴
∵二面角的大小为 ∴,解得:
∴的长度为. …………10分
18、(1)ABCD是矩形,所以,BC⊥CD,
VD⊥平面ABCD,所以,VD⊥BC,
又VD交CD于D
所以,BC⊥平面VCD
(2)AD∥BC,得AD∥平面VBC,
平面ADMN交平面VBC于MN
所以,AD∥MN
B
A
P
C
D
E
(第15题图)
P
A
B
C
D
E
(第15题图)
F
A
B
C
A1
B1
C1
F
E
D
A
B
C
D
S
M
N
(第16题)
同课章节目录
