五年级下册数学一课一练-2.2展开与折叠 北师大版(2014秋)(含答案)
文档属性
| 名称 | 五年级下册数学一课一练-2.2展开与折叠 北师大版(2014秋)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 107.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-11 22:26:49 | ||
图片预览

文档简介
五年级下册数学一课一练-2.2展开与折叠
一、单选题
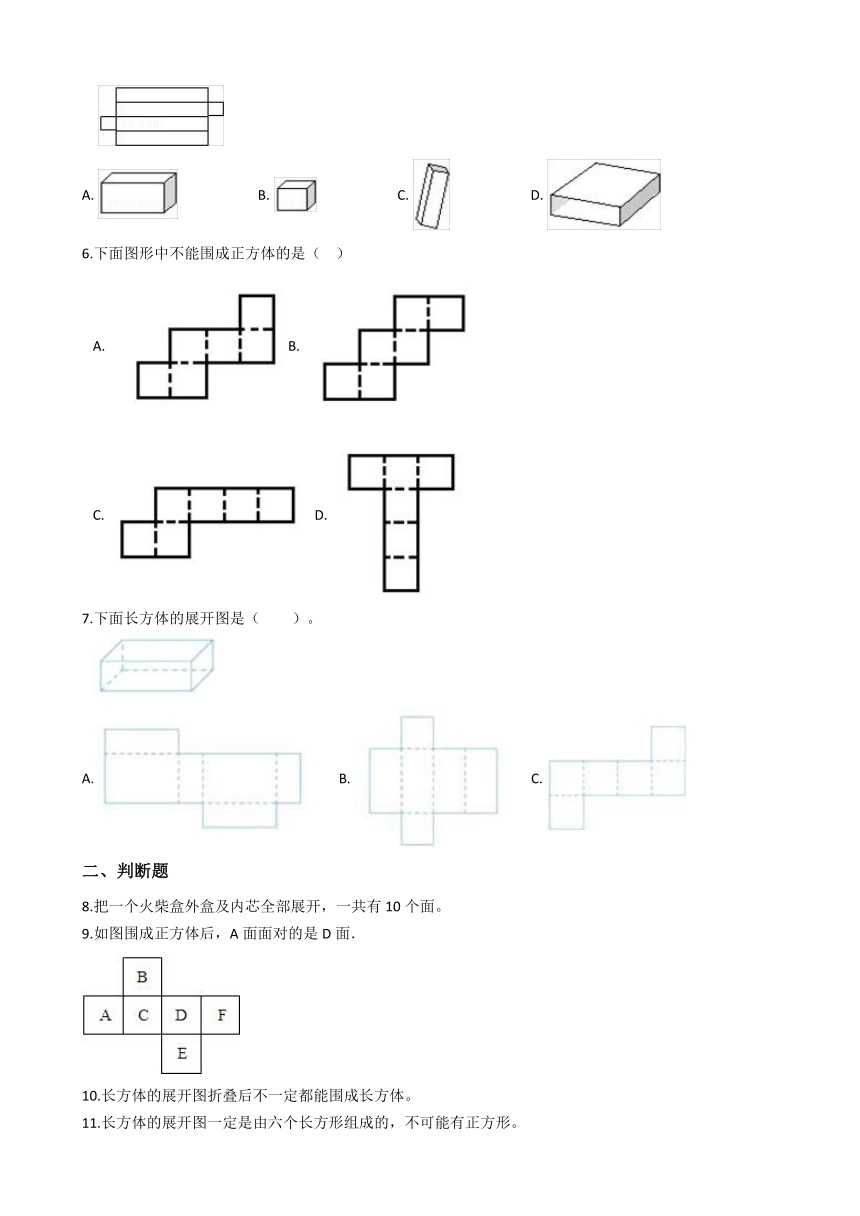
1.将图中的硬纸板沿虚线折叠成为一个正方体,这个正方体6号面的背面是(?? )
/
A.2号 B.3号 C.1号 D.4号
2.观察:和字母D相对的面是( ?),F面对(? )
/
A.?A,B ???????????????????????????????????/B.?C , A ???????????????????????????????????/C.?B,E
3.下面三个图形中不能拼成正方体的是(? )
A.?/??????????????????????????/B.?/??????????????????????????/C.?/
4.将下面的硬纸板沿虚线折起来成一个正方体这个正方体的3号面的对面是( ??)号面
/
A.2 B.4 C.5 D.6
5.如图最有可能是( )的展开图.
/
A.?/ ?????????????????????B.?/ ?????????????????????C.?/ ?????????????????????D.?/
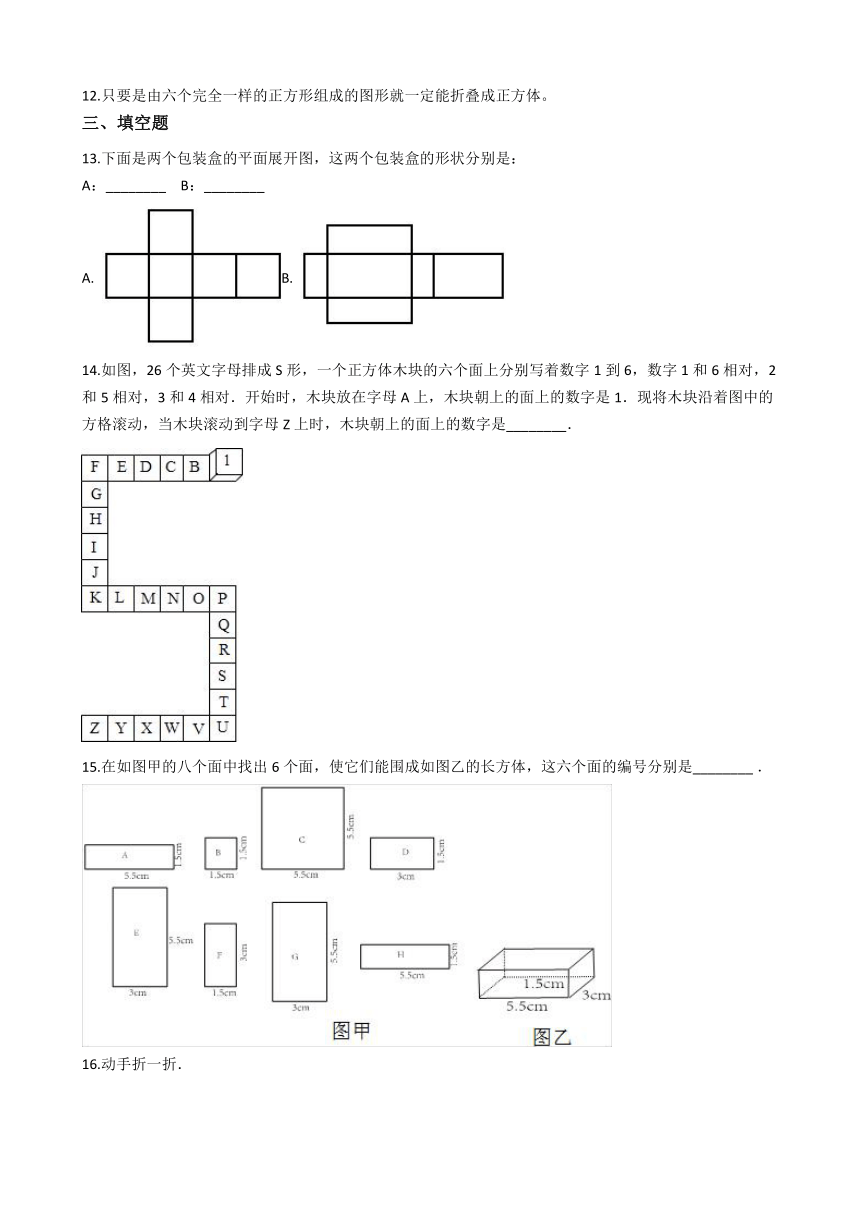
6.下面图形中不能围成正方体的是(?? )
A.?/B.?/ C.?/D.?/
7.下面长方体的展开图是(??????? )。
? /
A.?/ ?????/B.?/ ?????/C.?/
二、判断题
8.把一个火柴盒外盒及内芯全部展开,一共有10个面。
9.如图围成正方体后,A面面对的是D面. /
10.长方体的展开图折叠后不一定都能围成长方体。
11.长方体的展开图一定是由六个长方形组成的,不可能有正方形。
12.只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。
三、填空题
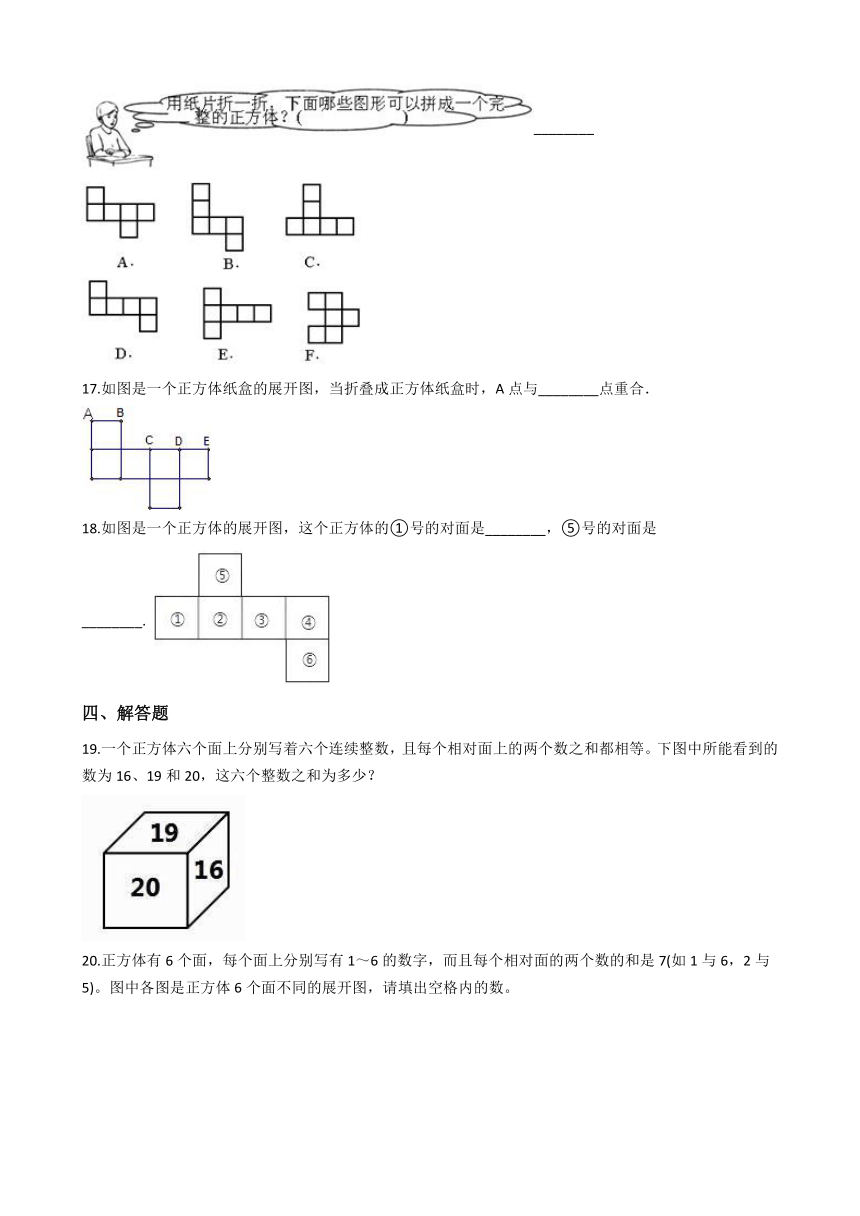
13.下面是两个包装盒的平面展开图,这两个包装盒的形状分别是:
A:________?? B:________
A. /B. /
14.如图,26个英文字母排成S形,一个正方体木块的六个面上分别写着数字1到6,数字1和6相对,2和5相对,3和4相对.开始时,木块放在字母A上,木块朝上的面上的数字是1.现将木块沿着图中的方格滚动,当木块滚动到字母Z上时,木块朝上的面上的数字是________. /
15.在如图甲的八个面中找出6个面,使它们能围成如图乙的长方体,这六个面的编号分别是________?. /
16.动手折一折.
/________ /
17.如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与________点重合. /
18.如图是一个正方体的展开图,这个正方体的①号的对面是________,⑤号的对面是________./
四、解答题
19.一个正方体六个面上分别写着六个连续整数,且每个相对面上的两个数之和都相等。下图中所能看到的数为16、19和20,这六个整数之和为多少?
/
20.正方体有6个面,每个面上分别写有1~6的数字,而且每个相对面的两个数的和是7(如1与6,2与5)。图中各图是正方体6个面不同的展开图,请填出空格内的数。
/
五、应用题
21.右面是一个纸盒的展开图(无盖). (1)做这个纸盒需要多大的纸板? (2)这个纸盒的容积是多少?(纸板厚度忽略不计) /
22.下两幅图是不完整的正方体展开图,请分别把它们补充成完整的正方体展开图. /
答案解析部分
一、单选题
1.【答案】A
【解析】【解答】解:6号面的背面应该是2号。 故答案为:A。
【分析】如果2为底面,则3是后面,5是前面,1是左面,4是右面,6是上面,6与2是相对的面。
2.【答案】C
【解析】【分析】根据观察规律,里面有一个小正方体,只有在上面看才能看到,所以一共有3个;
能看到的物体,该面应该与视线垂直对应,所以,在右边看小正方体只能看到两个面,所以选择A.
3.【答案】A
【解析】【解答】解:图B和图C是“1 4 1”结构,是正方体的展开图,图A不是正方体的展开图;
故选:A.
【分析】根据正方体的表面展开图共有11种情况,B和C是“1 4 1”结构,,即中间四个正方形围成正方体的侧面,上、下各一个为正方体的上、下底;A不符合正方体展开图的11种特征,不是正方体的展开图由此可进行选择.本题是考查正方体的展开图,培养学生的观察和空间想象能力.
4.【答案】C
【解析】【解答】解:这个正方体的3号面的对面是5号面。 故答案为:C。
【分析】如果是2号为底面,则1号是左面,4号是右面;3号是后面,5号是前面;6号是上面。由此确定相对的面即可。
5.【答案】C
【解析】【解答】解:由分析得出:如图最有可能是C图的展开图.
故选:C.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
6.【答案】C
【解析】【解答】解:不能围成正方体的是C。 故答案为:C。
【分析】把这些面折叠起来,如果没有重叠的面就能围成正方体,如果有重叠的面就不能围成正方体。
7.【答案】A
【解析】【解答】 /的展开图是 /,故选A。
【分析】B项展开图有两个面是正方形,C项所有的面都是正方形,不符合长方体 /的特征。
二、判断题
8.【答案】错误
【解析】【解答】解:把一个火柴盒的外盒及内芯全部展开,一共有9个面。原题说法错误。 故答案为:错误【分析】火柴盒的外部没有两端的面,有4个面;内芯没有盖,有5个面。一共有9个面。
9.【答案】正确
【解析】【解答】解:如图, / 围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面; 因此,原题说法正确; 故答案为:正确 【分析】如图,是正方体的展开图,属于“1 4 1”结构,围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
10.【答案】错误
【解析】【解答】长方体的展开图折叠后不一定都能围成长方体。说法错误。故答案为:错误 【分析】长方体的展开图沿着它的棱剪开后所得,那么它折叠后一定都能围成长方体。
11.【答案】错误
【解析】【解答】长方体的6个面在特殊情况下有可能有2个面是正方形。所以长方体的展开图也有可能有两个面是正方形。故答案为:错误 【分析】6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形是长方体。
12.【答案】错误
【解析】【解答】只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。说法错误。故答案为:错误 【分析】六个完全一样的正方形组成的图形不一定能折叠成正方体,还主要看这六个正方形是怎样排列的,如果一行排6个,就不能折叠成正方体。
三、填空题
13.【答案】是正方体;是长方体
【解析】【解答】解:根据图形的特征可知:A是正方体,B是长方体。 故答案为:是正方体;是长方体。
【分析】A图中6个面都是正方形,一定是正方体;B图中有长方形的面,一定是长方体。
14.【答案】不一定
【解析】【解答】解:当木块滚动到字母Z上时,木块朝上的面上的数字是不一定; 故答案为:不一定. 【分析】虽然木块滚动一次,数字和字母都会变动一次,2与5的位置,及3与4的位置不同,最后滚动到字母Z时,朝上的数字不一写.此题属于操作题,动手操作一下即可解决问题.注意几个转变处木块滚动的方向.
15.【答案】E、G、A、H、D、F
【解析】【解答】解:由图乙可知:这个长方体的长是5.5厘米、宽是3厘米、高是1.5厘米, 所以选择E、G作为长方体的上下面,A、H作为长方体的前后面,D、F在为长方体的左右面, 故答案为:E、G、A、H、D、F. 【分析】根据长方体的特征:长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.此题考查的目的是理解掌握长方体的特征.
16.【答案】A,D,E
【解析】【解答】解:B、C、F中拼摆后会有重叠的面,这几个都不能拼成一个完整的正方体;A、D、E中拼摆后会拼成一个完整的正方体. 故答案为:A;D;E
【分析】可以把一个面作为底面,如果折后没有重叠的面就能拼出一个完整的正方体,由此判断即可.
17.【答案】D
【解析】【解答】解:由分析可得,当折叠成正方体纸盒时,A点与D点重合. 故答案为:D. 【分析】此题属于正方体展开图中的1﹣4﹣1型,折叠成正方体后,A点与D点重合.据此选择.此题考查正方体的展开图,解决此题的关键是把展开图折成长方体,找到重合的点.
18.【答案】③;⑥
【解析】【解答】解:根据分析可得:这个正方体的①号的对面是③,⑤号的对面是⑥. 故答案为:③,⑥. 【分析】假设把②作为底面,则①就是左面,③就是右面;⑤是后面,则⑥就是前面;由此判断相对的面即可.
四、解答题
19.【答案】解:16+17+18+19+20+21=111答:这六个整数之和为111。
【解析】【分析】从16、19、20可以确定其中的5个数是16、17、18、19、20,第6个数是15还是21 ,分析:如果是15,16和19必须是对面,和题干中图形不符,所以这6个整数是16、17、18、19、20、21.
20.【答案】解:
/
【解析】【分析】先确定一个底面,然后判断出图形的左右面、前后面、上下面,左右相对,前后相对,上下相对,填入相应的数字即可。
五、应用题
21.【答案】解:长方体的长是30厘米,宽是30厘米,高是12厘米, 表面积为: 30×12×4+30×30 =1440+900 =2340(平方厘米) 体积为:30×30×12=10800(立方厘米). 答:做这个纸盒需要2340平方厘米的纸板;这个纸盒的容积是10800立方厘米.
【解析】【分析】由展开图得出长方体的长是30厘米,宽是30厘米,高是12厘米;再根据长方体表面积和体积的公式计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
22.【答案】解:根据分析画图如下: 故答案为: /
【解析】【分析】根据正方体展开图的11种特征,左图再在四个正方形的下面添上一个正方形,即成为正方体展开图的“1 4 1”结构,就是一个完整的正方体展开图;右图在下行左边添上一个正方形,即成为正方体展开图的“2 2 2”结构,就是一个完整的正方体展开图.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
一、单选题
1.将图中的硬纸板沿虚线折叠成为一个正方体,这个正方体6号面的背面是(?? )
/
A.2号 B.3号 C.1号 D.4号
2.观察:和字母D相对的面是( ?),F面对(? )
/
A.?A,B ???????????????????????????????????/B.?C , A ???????????????????????????????????/C.?B,E
3.下面三个图形中不能拼成正方体的是(? )
A.?/??????????????????????????/B.?/??????????????????????????/C.?/
4.将下面的硬纸板沿虚线折起来成一个正方体这个正方体的3号面的对面是( ??)号面
/
A.2 B.4 C.5 D.6
5.如图最有可能是( )的展开图.
/
A.?/ ?????????????????????B.?/ ?????????????????????C.?/ ?????????????????????D.?/
6.下面图形中不能围成正方体的是(?? )
A.?/B.?/ C.?/D.?/
7.下面长方体的展开图是(??????? )。
? /
A.?/ ?????/B.?/ ?????/C.?/
二、判断题
8.把一个火柴盒外盒及内芯全部展开,一共有10个面。
9.如图围成正方体后,A面面对的是D面. /
10.长方体的展开图折叠后不一定都能围成长方体。
11.长方体的展开图一定是由六个长方形组成的,不可能有正方形。
12.只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。
三、填空题
13.下面是两个包装盒的平面展开图,这两个包装盒的形状分别是:
A:________?? B:________
A. /B. /
14.如图,26个英文字母排成S形,一个正方体木块的六个面上分别写着数字1到6,数字1和6相对,2和5相对,3和4相对.开始时,木块放在字母A上,木块朝上的面上的数字是1.现将木块沿着图中的方格滚动,当木块滚动到字母Z上时,木块朝上的面上的数字是________. /
15.在如图甲的八个面中找出6个面,使它们能围成如图乙的长方体,这六个面的编号分别是________?. /
16.动手折一折.
/________ /
17.如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与________点重合. /
18.如图是一个正方体的展开图,这个正方体的①号的对面是________,⑤号的对面是________./
四、解答题
19.一个正方体六个面上分别写着六个连续整数,且每个相对面上的两个数之和都相等。下图中所能看到的数为16、19和20,这六个整数之和为多少?
/
20.正方体有6个面,每个面上分别写有1~6的数字,而且每个相对面的两个数的和是7(如1与6,2与5)。图中各图是正方体6个面不同的展开图,请填出空格内的数。
/
五、应用题
21.右面是一个纸盒的展开图(无盖). (1)做这个纸盒需要多大的纸板? (2)这个纸盒的容积是多少?(纸板厚度忽略不计) /
22.下两幅图是不完整的正方体展开图,请分别把它们补充成完整的正方体展开图. /
答案解析部分
一、单选题
1.【答案】A
【解析】【解答】解:6号面的背面应该是2号。 故答案为:A。
【分析】如果2为底面,则3是后面,5是前面,1是左面,4是右面,6是上面,6与2是相对的面。
2.【答案】C
【解析】【分析】根据观察规律,里面有一个小正方体,只有在上面看才能看到,所以一共有3个;
能看到的物体,该面应该与视线垂直对应,所以,在右边看小正方体只能看到两个面,所以选择A.
3.【答案】A
【解析】【解答】解:图B和图C是“1 4 1”结构,是正方体的展开图,图A不是正方体的展开图;
故选:A.
【分析】根据正方体的表面展开图共有11种情况,B和C是“1 4 1”结构,,即中间四个正方形围成正方体的侧面,上、下各一个为正方体的上、下底;A不符合正方体展开图的11种特征,不是正方体的展开图由此可进行选择.本题是考查正方体的展开图,培养学生的观察和空间想象能力.
4.【答案】C
【解析】【解答】解:这个正方体的3号面的对面是5号面。 故答案为:C。
【分析】如果是2号为底面,则1号是左面,4号是右面;3号是后面,5号是前面;6号是上面。由此确定相对的面即可。
5.【答案】C
【解析】【解答】解:由分析得出:如图最有可能是C图的展开图.
故选:C.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
6.【答案】C
【解析】【解答】解:不能围成正方体的是C。 故答案为:C。
【分析】把这些面折叠起来,如果没有重叠的面就能围成正方体,如果有重叠的面就不能围成正方体。
7.【答案】A
【解析】【解答】 /的展开图是 /,故选A。
【分析】B项展开图有两个面是正方形,C项所有的面都是正方形,不符合长方体 /的特征。
二、判断题
8.【答案】错误
【解析】【解答】解:把一个火柴盒的外盒及内芯全部展开,一共有9个面。原题说法错误。 故答案为:错误【分析】火柴盒的外部没有两端的面,有4个面;内芯没有盖,有5个面。一共有9个面。
9.【答案】正确
【解析】【解答】解:如图, / 围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面; 因此,原题说法正确; 故答案为:正确 【分析】如图,是正方体的展开图,属于“1 4 1”结构,围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
10.【答案】错误
【解析】【解答】长方体的展开图折叠后不一定都能围成长方体。说法错误。故答案为:错误 【分析】长方体的展开图沿着它的棱剪开后所得,那么它折叠后一定都能围成长方体。
11.【答案】错误
【解析】【解答】长方体的6个面在特殊情况下有可能有2个面是正方形。所以长方体的展开图也有可能有两个面是正方形。故答案为:错误 【分析】6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形是长方体。
12.【答案】错误
【解析】【解答】只要是由六个完全一样的正方形组成的图形就一定能折叠成正方体。说法错误。故答案为:错误 【分析】六个完全一样的正方形组成的图形不一定能折叠成正方体,还主要看这六个正方形是怎样排列的,如果一行排6个,就不能折叠成正方体。
三、填空题
13.【答案】是正方体;是长方体
【解析】【解答】解:根据图形的特征可知:A是正方体,B是长方体。 故答案为:是正方体;是长方体。
【分析】A图中6个面都是正方形,一定是正方体;B图中有长方形的面,一定是长方体。
14.【答案】不一定
【解析】【解答】解:当木块滚动到字母Z上时,木块朝上的面上的数字是不一定; 故答案为:不一定. 【分析】虽然木块滚动一次,数字和字母都会变动一次,2与5的位置,及3与4的位置不同,最后滚动到字母Z时,朝上的数字不一写.此题属于操作题,动手操作一下即可解决问题.注意几个转变处木块滚动的方向.
15.【答案】E、G、A、H、D、F
【解析】【解答】解:由图乙可知:这个长方体的长是5.5厘米、宽是3厘米、高是1.5厘米, 所以选择E、G作为长方体的上下面,A、H作为长方体的前后面,D、F在为长方体的左右面, 故答案为:E、G、A、H、D、F. 【分析】根据长方体的特征:长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.此题考查的目的是理解掌握长方体的特征.
16.【答案】A,D,E
【解析】【解答】解:B、C、F中拼摆后会有重叠的面,这几个都不能拼成一个完整的正方体;A、D、E中拼摆后会拼成一个完整的正方体. 故答案为:A;D;E
【分析】可以把一个面作为底面,如果折后没有重叠的面就能拼出一个完整的正方体,由此判断即可.
17.【答案】D
【解析】【解答】解:由分析可得,当折叠成正方体纸盒时,A点与D点重合. 故答案为:D. 【分析】此题属于正方体展开图中的1﹣4﹣1型,折叠成正方体后,A点与D点重合.据此选择.此题考查正方体的展开图,解决此题的关键是把展开图折成长方体,找到重合的点.
18.【答案】③;⑥
【解析】【解答】解:根据分析可得:这个正方体的①号的对面是③,⑤号的对面是⑥. 故答案为:③,⑥. 【分析】假设把②作为底面,则①就是左面,③就是右面;⑤是后面,则⑥就是前面;由此判断相对的面即可.
四、解答题
19.【答案】解:16+17+18+19+20+21=111答:这六个整数之和为111。
【解析】【分析】从16、19、20可以确定其中的5个数是16、17、18、19、20,第6个数是15还是21 ,分析:如果是15,16和19必须是对面,和题干中图形不符,所以这6个整数是16、17、18、19、20、21.
20.【答案】解:
/
【解析】【分析】先确定一个底面,然后判断出图形的左右面、前后面、上下面,左右相对,前后相对,上下相对,填入相应的数字即可。
五、应用题
21.【答案】解:长方体的长是30厘米,宽是30厘米,高是12厘米, 表面积为: 30×12×4+30×30 =1440+900 =2340(平方厘米) 体积为:30×30×12=10800(立方厘米). 答:做这个纸盒需要2340平方厘米的纸板;这个纸盒的容积是10800立方厘米.
【解析】【分析】由展开图得出长方体的长是30厘米,宽是30厘米,高是12厘米;再根据长方体表面积和体积的公式计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
22.【答案】解:根据分析画图如下: 故答案为: /
【解析】【分析】根据正方体展开图的11种特征,左图再在四个正方形的下面添上一个正方形,即成为正方体展开图的“1 4 1”结构,就是一个完整的正方体展开图;右图在下行左边添上一个正方形,即成为正方体展开图的“2 2 2”结构,就是一个完整的正方体展开图.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
