数学人教A版选修2-1 2.2.1 椭圆及其标准方程 课件(23张)
文档属性
| 名称 | 数学人教A版选修2-1 2.2.1 椭圆及其标准方程 课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1016.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-12 00:00:00 | ||
图片预览




文档简介
课件23张PPT。2.2.1 椭圆及其标准方程
(一) 生活中的椭圆生活中的椭圆 在前面圆的方程中我们知道:平面内到一定点的距离为常数的点的轨迹是圆改为两个定点呢?数 学 实 验[1]在平面内,任取两个定点F1、F2 ;
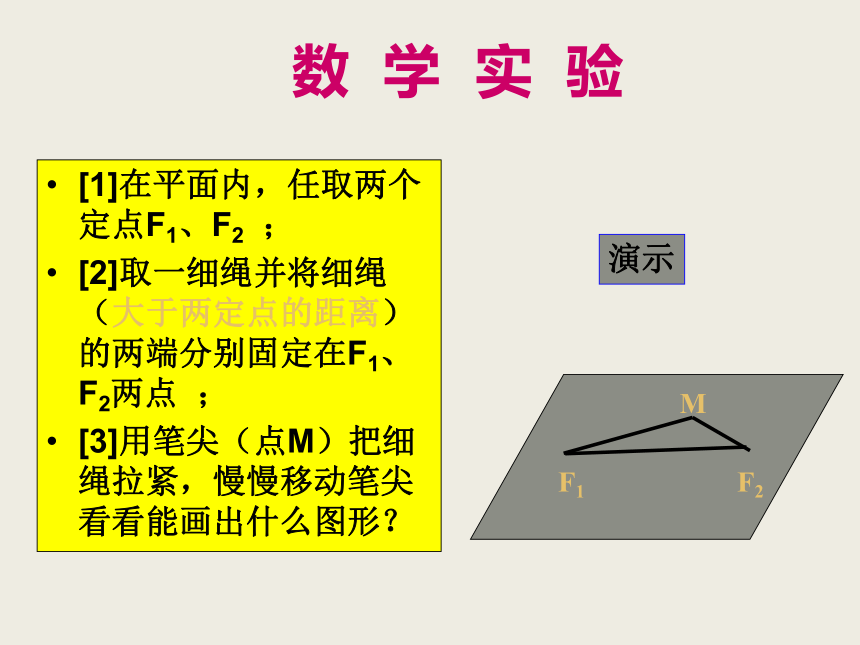
[2]取一细绳并将细绳(大于两定点的距离)的两端分别固定在F1、F2两点 ;
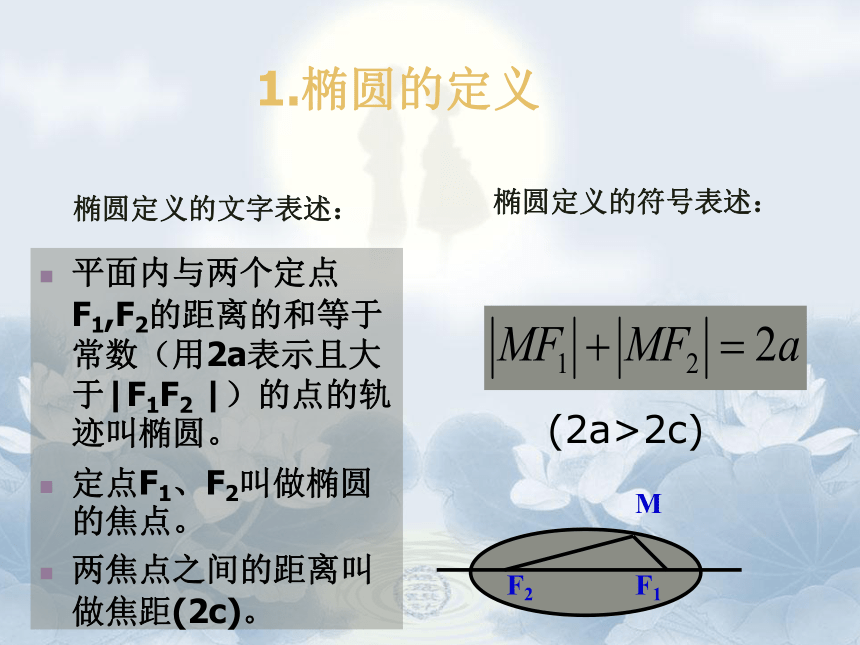
[3]用笔尖(点M)把细绳拉紧,慢慢移动笔尖看看能画出什么图形?演示F1F2请你为椭圆下一个定义 想想看,这一过程中什么变化了,什么没有变?1.椭圆的定义平面内与两个定点F1,F2的距离的和等于常数(用2a表示且大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。椭圆定义的文字表述:椭圆定义的符号表述:MF2F1数 学 实 验[1]在平面内,任取两个定点F1、F2 ;
[2]取一细绳并将细绳(大于两定点的距离)的两端分别固定在F1、F2两点 ;
[3]用笔尖(点M)把细绳拉紧,慢慢移动笔尖看看能画出什么图形?若改为小于或等于将是什么情况?演示1演示2 结论:
1.当绳长大于两定点F1,F2间的距离时,轨迹是椭圆。
2.当绳长等于两定点F1,F2间的距离时,轨迹是以F1,F2为端点的线段。
3.当绳长小于两定点F1,F2间的距离时,不能构成图形。? 求动点轨迹方程的一般方法:(1)建系设点
(2)列式
(3)代换、化简
(4)审查坐标法2.求椭圆的方程:? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常利用“对称性”方案一2.求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得:代入坐标整理得两边再平方,得移项,平方总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:3.椭圆的标准方程: 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)定 义注:共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.Y椭圆的标准方程的认识:(1)“椭圆的标准方程”是个专有名词,专指本节介绍的两
个方程,方程形式是固定的。(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(4)由椭圆的标准方程可以求出三个参数a、b、c的值。(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上,即“椭圆的焦点看分母,谁大在谁上”例1、填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________例题精析543(3,0)、(-3,0)620判断椭圆标准方程的焦点所在轴的方法:
看分母,谁大在谁上练习1:判定下列椭圆的焦点在哪条轴上?并指明a2、b2,写出焦点坐标答:在 X 轴。(-3,0)和
(3,0)答:在 y 轴。(0,-5)和
(0,5)答:在y 轴。(0,-1)和
(0,1)(2)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为:__________,焦距
等于_________;
若曲线上一点P到下焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________21(0,-1)、(0,1)2P例1、填空:练习2:将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标例2.已知椭圆的两个焦点的坐标分别是(-2,0),
(2,0),并且经过点 ,求它的标准方程.待定系数法 两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10。解:因为椭圆的焦点在X轴上,所以可设它的方程
为:?2a=10,2c=8即 a=5,c=4故 b2=a2-c2=52-42=9所以椭圆的标准方程为:练习、求满足下列条件的椭圆的标准方程: 看分母,谁大在谁上a2-c2=b2(a>b>0)总结回顾 |MF1 |+|MF2|=2a(2a>2c)
(一) 生活中的椭圆生活中的椭圆 在前面圆的方程中我们知道:平面内到一定点的距离为常数的点的轨迹是圆改为两个定点呢?数 学 实 验[1]在平面内,任取两个定点F1、F2 ;
[2]取一细绳并将细绳(大于两定点的距离)的两端分别固定在F1、F2两点 ;
[3]用笔尖(点M)把细绳拉紧,慢慢移动笔尖看看能画出什么图形?演示F1F2请你为椭圆下一个定义 想想看,这一过程中什么变化了,什么没有变?1.椭圆的定义平面内与两个定点F1,F2的距离的和等于常数(用2a表示且大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。椭圆定义的文字表述:椭圆定义的符号表述:MF2F1数 学 实 验[1]在平面内,任取两个定点F1、F2 ;
[2]取一细绳并将细绳(大于两定点的距离)的两端分别固定在F1、F2两点 ;
[3]用笔尖(点M)把细绳拉紧,慢慢移动笔尖看看能画出什么图形?若改为小于或等于将是什么情况?演示1演示2 结论:
1.当绳长大于两定点F1,F2间的距离时,轨迹是椭圆。
2.当绳长等于两定点F1,F2间的距离时,轨迹是以F1,F2为端点的线段。
3.当绳长小于两定点F1,F2间的距离时,不能构成图形。? 求动点轨迹方程的一般方法:(1)建系设点
(2)列式
(3)代换、化简
(4)审查坐标法2.求椭圆的方程:? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常利用“对称性”方案一2.求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得:代入坐标整理得两边再平方,得移项,平方总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:3.椭圆的标准方程: 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)定 义注:共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.Y椭圆的标准方程的认识:(1)“椭圆的标准方程”是个专有名词,专指本节介绍的两
个方程,方程形式是固定的。(3)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(4)由椭圆的标准方程可以求出三个参数a、b、c的值。(2)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上,即“椭圆的焦点看分母,谁大在谁上”例1、填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________例题精析543(3,0)、(-3,0)620判断椭圆标准方程的焦点所在轴的方法:
看分母,谁大在谁上练习1:判定下列椭圆的焦点在哪条轴上?并指明a2、b2,写出焦点坐标答:在 X 轴。(-3,0)和
(3,0)答:在 y 轴。(0,-5)和
(0,5)答:在y 轴。(0,-1)和
(0,1)(2)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为:__________,焦距
等于_________;
若曲线上一点P到下焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________21(0,-1)、(0,1)2P例1、填空:练习2:将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标例2.已知椭圆的两个焦点的坐标分别是(-2,0),
(2,0),并且经过点 ,求它的标准方程.待定系数法 两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10。解:因为椭圆的焦点在X轴上,所以可设它的方程
为:?2a=10,2c=8即 a=5,c=4故 b2=a2-c2=52-42=9所以椭圆的标准方程为:练习、求满足下列条件的椭圆的标准方程: 看分母,谁大在谁上a2-c2=b2(a>b>0)总结回顾 |MF1 |+|MF2|=2a(2a>2c)
