2018年优课系列高中数学人教A版选修2-1 3.2 立体几何中的向量方法 课件(20张)
文档属性
| 名称 | 2018年优课系列高中数学人教A版选修2-1 3.2 立体几何中的向量方法 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-12 00:00:00 | ||
图片预览






文档简介
课件20张PPT。人教A版选修2-1 高二数学空间向量与立体几何
--空间角学习目标1、能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题。
2、了解向量方法在研究立体几何问题中的应用。1.两条异面直线所成的角
(1)定义:设a,b是两条异面直线,过空间任一点O作直线a ′∥a, b ′∥b,则a ′, b ′所夹的锐角或直角叫a与b所成的角.
(2)范围:
(3)向量求法:设直线a、b的方向向量为 ,其夹角为 ,则有
(4)注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角求得,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.空间三种角的向量求解方法1.两条异面直线所成的角
(1)定义:设a,b是两条异面直线,过空间任一点O作直线a ′∥a, b ′∥b,则a ′, b ′所夹的锐角或直角叫a与b所成的角.
(2)范围:
(3)向量求法:设直线a、b的方向向量为 ,其夹角为 ,则有
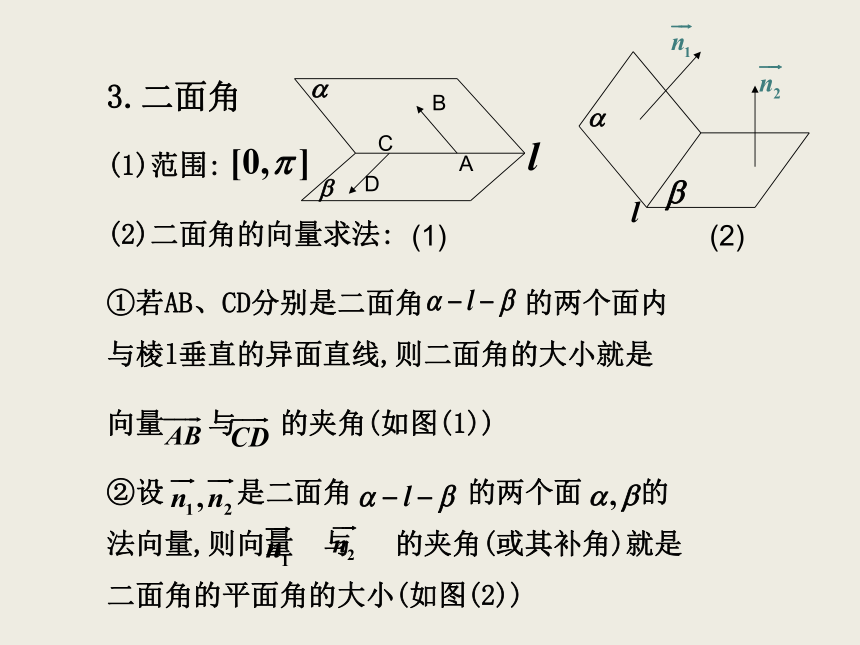
(4)注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角求得,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.考点回顾:3.二面角
(1)范围:
(2)二面角的向量求法:
①若AB、CD分别是二面角 的两个面内与棱l垂直的异面直线,则二面角的大小就是
向量 与 的夹角(如图(1))
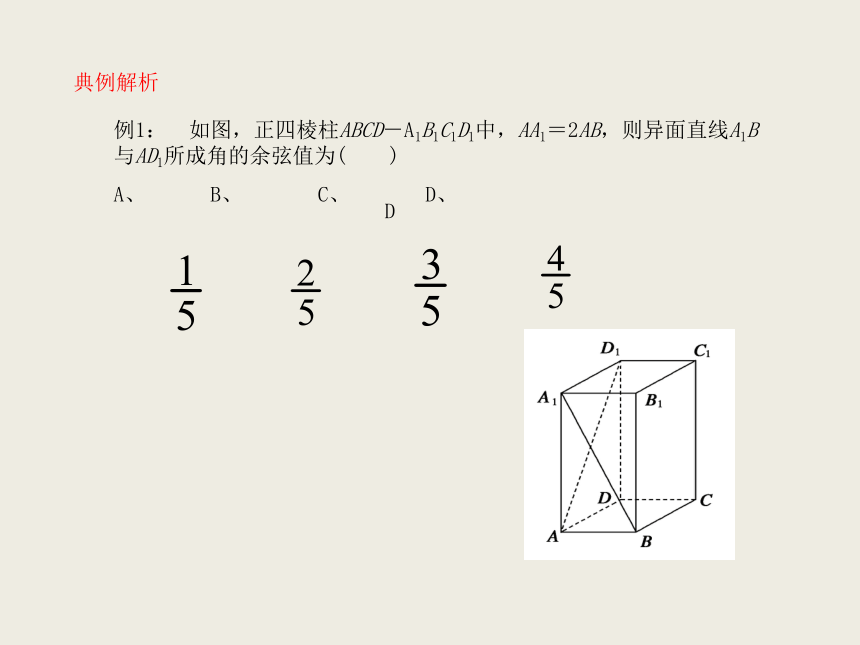
②设 是二面角 的两个面 的法向量,则向量 与 的夹角(或其补角)就是二面角的平面角的大小(如图(2))(1)(2)典例解析 例1: 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
A、 B、 C、 D、
D变式1:正四棱锥P-ABCD的所有棱长相等,E为PC的中点,那么异面直线BE与PA所成角的余弦值等于( )
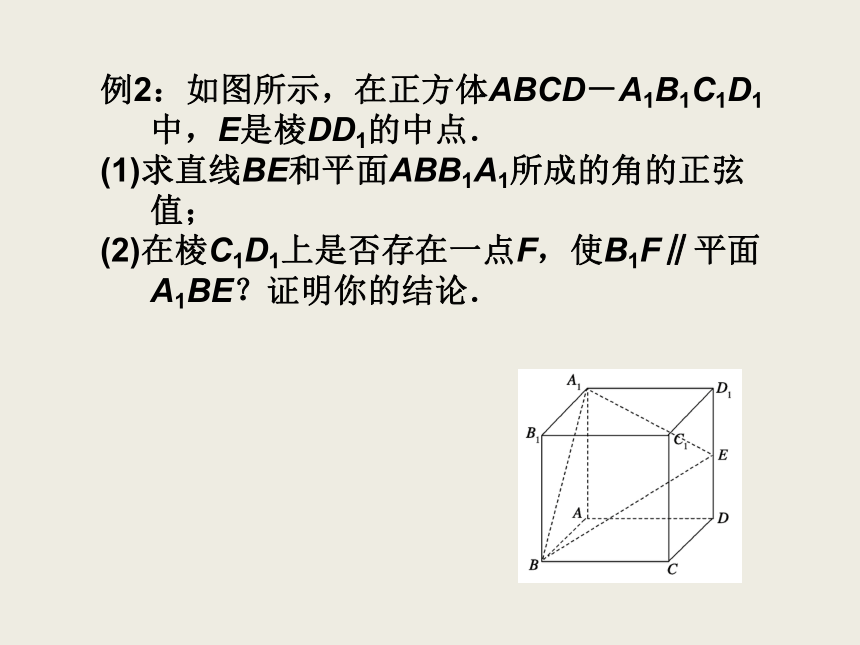
A、 B、 C、 D、D例2:如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
(1)求直线BE和平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.解析:解法1:(1)如图,以A为坐标原点AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,用空间向量解决立体几何问题的“三步曲”。(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)(进行向量运算)(回到图形问题)小 结小 结1.异面直线所成角: 2.直线与平面所成角: 3.二面角:关键:观察二面角的范围1、正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的余弦值为( )
A、 B、 C、 D、
2、(2009年四川)已知正三棱柱ABC-A1B1C1的各条棱都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 当堂检测 M3、如图,四棱锥P—ABCD中,底面ABCD为平行四
边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。分析:(1)要证明线线垂直只要证明线面垂直或者用向量去证明;(2)求二面角的余弦只需建立适当的坐标系,有空间向量来完成。解:(1)证明:在三角形ABD中,因为该三角形为直角三角形,所以, (2)建立如图的坐标系,设点的坐标分别是则 设平面PAB的法向量为 , 所以, 同理设平面PBC的法向量为 ,取得,取得 于是, 因此二面角的余弦值是 课下作业1、如图5,在圆锥PO中,已知PO= ,⊙O的直径AB=2,C是弧AB的中点,D是AC的中点.
(Ⅰ)证明:平面POD 平面PAC;
(Ⅱ)求二面角B-PA-C 的余弦值。2、如图所示,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
(1)证明:M是侧棱SC的中点;
(2)求二面角S-AM-B的余弦值.
--空间角学习目标1、能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题。
2、了解向量方法在研究立体几何问题中的应用。1.两条异面直线所成的角
(1)定义:设a,b是两条异面直线,过空间任一点O作直线a ′∥a, b ′∥b,则a ′, b ′所夹的锐角或直角叫a与b所成的角.
(2)范围:
(3)向量求法:设直线a、b的方向向量为 ,其夹角为 ,则有
(4)注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角求得,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.空间三种角的向量求解方法1.两条异面直线所成的角
(1)定义:设a,b是两条异面直线,过空间任一点O作直线a ′∥a, b ′∥b,则a ′, b ′所夹的锐角或直角叫a与b所成的角.
(2)范围:
(3)向量求法:设直线a、b的方向向量为 ,其夹角为 ,则有
(4)注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角求得,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.考点回顾:3.二面角
(1)范围:
(2)二面角的向量求法:
①若AB、CD分别是二面角 的两个面内与棱l垂直的异面直线,则二面角的大小就是
向量 与 的夹角(如图(1))
②设 是二面角 的两个面 的法向量,则向量 与 的夹角(或其补角)就是二面角的平面角的大小(如图(2))(1)(2)典例解析 例1: 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
A、 B、 C、 D、
D变式1:正四棱锥P-ABCD的所有棱长相等,E为PC的中点,那么异面直线BE与PA所成角的余弦值等于( )
A、 B、 C、 D、D例2:如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
(1)求直线BE和平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.解析:解法1:(1)如图,以A为坐标原点AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,用空间向量解决立体几何问题的“三步曲”。(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)(进行向量运算)(回到图形问题)小 结小 结1.异面直线所成角: 2.直线与平面所成角: 3.二面角:关键:观察二面角的范围1、正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的余弦值为( )
A、 B、 C、 D、
2、(2009年四川)已知正三棱柱ABC-A1B1C1的各条棱都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 当堂检测 M3、如图,四棱锥P—ABCD中,底面ABCD为平行四
边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。分析:(1)要证明线线垂直只要证明线面垂直或者用向量去证明;(2)求二面角的余弦只需建立适当的坐标系,有空间向量来完成。解:(1)证明:在三角形ABD中,因为该三角形为直角三角形,所以, (2)建立如图的坐标系,设点的坐标分别是则 设平面PAB的法向量为 , 所以, 同理设平面PBC的法向量为 ,取得,取得 于是, 因此二面角的余弦值是 课下作业1、如图5,在圆锥PO中,已知PO= ,⊙O的直径AB=2,C是弧AB的中点,D是AC的中点.
(Ⅰ)证明:平面POD 平面PAC;
(Ⅱ)求二面角B-PA-C 的余弦值。2、如图所示,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
(1)证明:M是侧棱SC的中点;
(2)求二面角S-AM-B的余弦值.
