17.2勾股定理的逆定理(1)课件
图片预览








文档简介
人教版数学八年级下册
17.2勾股定理的逆定理(1)
1、什么叫命题?
2、命题的一般形式如何?
3、命题由几部分组成?
4、命题的真假?
命题“两直线平行,内错角相等”的一般形式是
,题设是
,结论是 。这是一个
命题。
如果两直线平行,那么内错角相等
两直线平行
内错角相等
真
交换该命题的题设和结论的位置看看得到一个什么新命题?
两个命题的题设与结论正好相反,像这样的两个命
题叫做互逆命题.如果把其中一个命题叫做原命题,那
么另一个命题叫做它的逆命题.
新命题: 。它的一般形式是 ,题设是 ,结论是 ,这是一个 命题。
内错角相等,两直线平行
两直线平行
如果内错角相等,那么两直线平行
真
内错角相等
两直线平行,内错角相等
(1)如果两个实数相等,那么它们的绝对值相等.
(2)全等三角形的对应角相等
(3)角的内部到角的两边距离相等的点在角的平分线上。
说出下列命题的逆命题,指出这些互逆命题的真假性。
逆命题:如果两个实数的绝对值相等,那么这两个实数相等.
逆命题:三个角对应相等的两个三角形是全等三角形.
逆命题:角平分线上的点到角两边的距离相等。
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
?
?
?
?
?
?
逆命题:
13,12,5; 6,8,10 ; 8,15,17。
证明:作Rt△A′B′C′,
使∠C′=900,A′C′=b,B′C′=a
∴∠C= ∠C′=900 △ABC是直角三角形
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
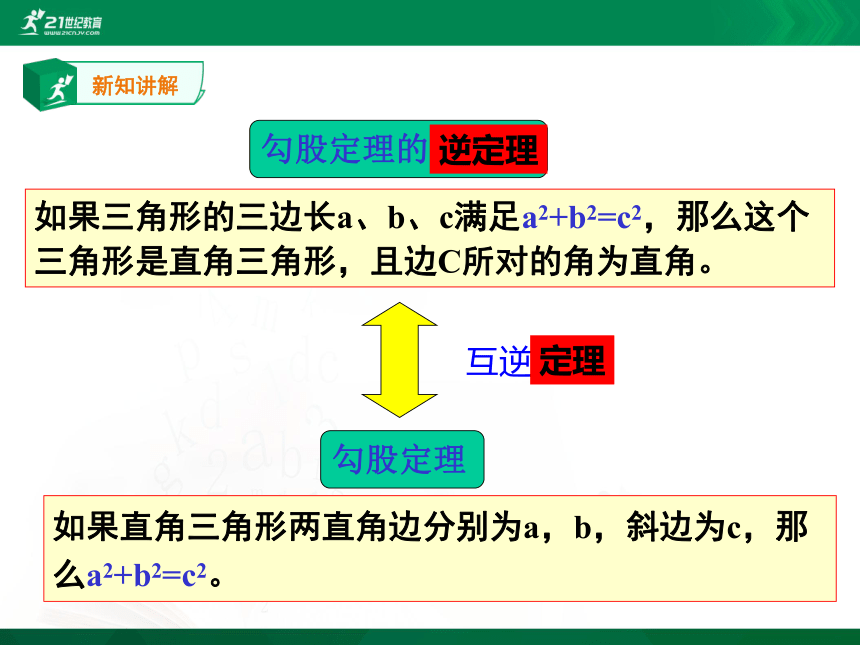
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2。
勾股定理
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
互逆命题
定理
逆定理
定理与逆定理:
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理。
两直线平行,内错角相等;内错角相等,两直线平行。
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方.
例1 判断由线段a,b,c组成的三角形是不是直角三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
观察3,4,5;6,8,10;9,12,15;12,16,20;18,24,30这几组勾股数?你发现它们有何联系?有什么样的猜想?
结论:若a,b,c是一组勾股数,那么ak,bk,ck
(k为正整数)也是一组勾股数.
1.下列各组线段中,不能够围成直角三角形是 ( )
A、9、12、15 B、8、15、17
C、7、24、25 D、6、8、9
D
看看谁更快!
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形
C
C
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形
证明:
∴△AEF是直角三角形,
∠AEF=90°
如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。
证明:∵AD是BC边上的中线,
∴BD=CD=1/2BC=5㎝
∵在△ABD中,AB=13,
BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形,且∠ ADB=900
∴∠ ADC=900, △ACD也是直角三角形。
∴AC=AB=13㎝
∴AB=AC
根据勾股定理得:
例3 已知 , 则由此为三边的三角形是 三角形。
解:依题意 x=6, y=8, z=10,
∵62+82=102
∴这个三角形是直角三角形
直角
练习 已知a,b,c为△ABC的三边,且满足
a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
直角三角形
例4 判断由线段a、b、c组成的三角形是不是直角三角形:a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)
∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4,
b2 = (m2 + n2 )2 = m4 + 2m2n2 + n4,
c2 = (2mn )2 = 4m2n2
又∵m4 - 2m2n2 + n4 + 4m2n2
= m4 + 2m2n2 + n4
∴ a2 + c2 = b2
即: 三角形是直角三角形
解:
练习 已知a.b.c为△ABC的三边,且满足
a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?___
(2) 错误原因是_________。
(3) 本题正确的结论是 。
(3)
a2- b2可能是0
直角三角形或等腰三角形
(2)原命题,逆命题之间有什么联系?
(1)勾股定理的逆定理的内容是什么?它有什么作用?
勾股定理的逆定理
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
作用:用于判断某个三角形是否是直角三角形。
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
(1)同旁内角互补,两直线平行。
逆命题是: 。
(2)如果两个角是直角,那么它们相等。
逆命题是: 。
(3)全等三角形的对应边相等。
逆命题是: 。
两直线平行,同旁内角互补
相等的两个角都是直角
三边对应相等的两个三角形全等
1.写出下列命题的逆命题:
2.如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
B
A
3.将直角三角形的三边长度扩大同样的倍数,则得到的三角形是( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
4.若一个三角形的三边长分别是5、12、13,那么这个三角形的面积是 。
30
5. 以?ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
直角
6.已知△ABC中∠A、∠B、∠C的对边分别是a、b、c,下面以a、b、c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
____ _____ ;
____ _____ ;
____ _____ ;
____ _____ ;
____ _____ .
不是
是
是
是
是
∠C=90°
∠B=90°
∠C=90°
∠B=90°
记住:小的两个数的平方和等于最大的数的平方时才是直角三角形!
7.△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
8.已知三角形ABC的三边长a,b,c为满足a+b=10,ab=18,c=8。此三角形是什么三角形?
直角三角形
是
1.必做题:教材习题17.2第1,2,3题.
2.选做题:教材习题17.2第7题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.2勾股定理的逆定理(1)
1、什么叫命题?
2、命题的一般形式如何?
3、命题由几部分组成?
4、命题的真假?
命题“两直线平行,内错角相等”的一般形式是
,题设是
,结论是 。这是一个
命题。
如果两直线平行,那么内错角相等
两直线平行
内错角相等
真
交换该命题的题设和结论的位置看看得到一个什么新命题?
两个命题的题设与结论正好相反,像这样的两个命
题叫做互逆命题.如果把其中一个命题叫做原命题,那
么另一个命题叫做它的逆命题.
新命题: 。它的一般形式是 ,题设是 ,结论是 ,这是一个 命题。
内错角相等,两直线平行
两直线平行
如果内错角相等,那么两直线平行
真
内错角相等
两直线平行,内错角相等
(1)如果两个实数相等,那么它们的绝对值相等.
(2)全等三角形的对应角相等
(3)角的内部到角的两边距离相等的点在角的平分线上。
说出下列命题的逆命题,指出这些互逆命题的真假性。
逆命题:如果两个实数的绝对值相等,那么这两个实数相等.
逆命题:三个角对应相等的两个三角形是全等三角形.
逆命题:角平分线上的点到角两边的距离相等。
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
?
?
?
?
?
?
逆命题:
13,12,5; 6,8,10 ; 8,15,17。
证明:作Rt△A′B′C′,
使∠C′=900,A′C′=b,B′C′=a
∴∠C= ∠C′=900 △ABC是直角三角形
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2。
勾股定理
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
互逆命题
定理
逆定理
定理与逆定理:
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理。
两直线平行,内错角相等;内错角相等,两直线平行。
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方.
例1 判断由线段a,b,c组成的三角形是不是直角三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
观察3,4,5;6,8,10;9,12,15;12,16,20;18,24,30这几组勾股数?你发现它们有何联系?有什么样的猜想?
结论:若a,b,c是一组勾股数,那么ak,bk,ck
(k为正整数)也是一组勾股数.
1.下列各组线段中,不能够围成直角三角形是 ( )
A、9、12、15 B、8、15、17
C、7、24、25 D、6、8、9
D
看看谁更快!
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形
C
C
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形
证明:
∴△AEF是直角三角形,
∠AEF=90°
如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。
证明:∵AD是BC边上的中线,
∴BD=CD=1/2BC=5㎝
∵在△ABD中,AB=13,
BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形,且∠ ADB=900
∴∠ ADC=900, △ACD也是直角三角形。
∴AC=AB=13㎝
∴AB=AC
根据勾股定理得:
例3 已知 , 则由此为三边的三角形是 三角形。
解:依题意 x=6, y=8, z=10,
∵62+82=102
∴这个三角形是直角三角形
直角
练习 已知a,b,c为△ABC的三边,且满足
a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
直角三角形
例4 判断由线段a、b、c组成的三角形是不是直角三角形:a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)
∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4,
b2 = (m2 + n2 )2 = m4 + 2m2n2 + n4,
c2 = (2mn )2 = 4m2n2
又∵m4 - 2m2n2 + n4 + 4m2n2
= m4 + 2m2n2 + n4
∴ a2 + c2 = b2
即: 三角形是直角三角形
解:
练习 已知a.b.c为△ABC的三边,且满足
a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?___
(2) 错误原因是_________。
(3) 本题正确的结论是 。
(3)
a2- b2可能是0
直角三角形或等腰三角形
(2)原命题,逆命题之间有什么联系?
(1)勾股定理的逆定理的内容是什么?它有什么作用?
勾股定理的逆定理
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
作用:用于判断某个三角形是否是直角三角形。
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
(1)同旁内角互补,两直线平行。
逆命题是: 。
(2)如果两个角是直角,那么它们相等。
逆命题是: 。
(3)全等三角形的对应边相等。
逆命题是: 。
两直线平行,同旁内角互补
相等的两个角都是直角
三边对应相等的两个三角形全等
1.写出下列命题的逆命题:
2.如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
B
A
3.将直角三角形的三边长度扩大同样的倍数,则得到的三角形是( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
4.若一个三角形的三边长分别是5、12、13,那么这个三角形的面积是 。
30
5. 以?ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
直角
6.已知△ABC中∠A、∠B、∠C的对边分别是a、b、c,下面以a、b、c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
____ _____ ;
____ _____ ;
____ _____ ;
____ _____ ;
____ _____ .
不是
是
是
是
是
∠C=90°
∠B=90°
∠C=90°
∠B=90°
记住:小的两个数的平方和等于最大的数的平方时才是直角三角形!
7.△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
8.已知三角形ABC的三边长a,b,c为满足a+b=10,ab=18,c=8。此三角形是什么三角形?
直角三角形
是
1.必做题:教材习题17.2第1,2,3题.
2.选做题:教材习题17.2第7题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
