高中数学苏教版选修1-1课件: 1.2 简单的逻辑联结词 章末总结复习课课件(38张)
文档属性
| 名称 | 高中数学苏教版选修1-1课件: 1.2 简单的逻辑联结词 章末总结复习课课件(38张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 15:54:42 | ||
图片预览











文档简介
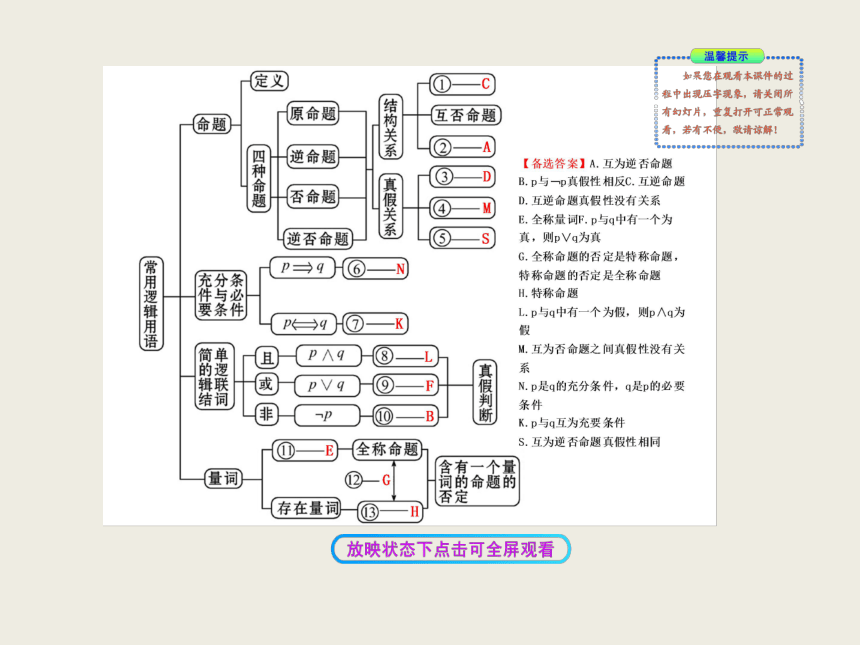
课件38张PPT。 章末总结复习课 对所学知识及时总结,将其构建成知识网络,既有助于整体把握知识结构,又利于加深对知识间内在联系的理解。下面是本阶段的知识结构图,请要求学生从后面的备选答案中选择准确内容,填在框图中的相应位置。 四种命题及关系
【技法点拨】
1.四种命题的写法
(1)对条件、结论不明显的命题,可以先将命题改写成“若p,则q”的形式后再进行转换.
(2)分清命题的条件和结论,然后进行互换和否定,即可得到原命题的逆命题、否命题和逆否命题.2.四种命题真假的判断方法
因为互为逆否命题的真假等价,所以判断四个命题的真假,只需判断原命题与逆命题(或否命题)的真假即可.【典例1】a,b,c为三个人,命题A:“如果b的年龄不是最大的,那么a的年龄最小”和命题B:“如果c的年龄不是最小的,那么a的年龄最大”都是真命题,则a,b,c的年龄的大小顺序是否能确定?请说明理由.
【解析】能确定.理由如下:
显然命题A和B的原命题的结论是矛盾的,因此应该从它的逆否命题来考虑.①由命题A为真可知,当b不是最大时,则a是最小的,即若c最大,则a最小,所以c>b>a;而它的逆否命题也为真,即“a不是最小,则b是最大”为真,所以b>a>c.总之由命题A为真可知:c>b>a或b>a>c.
②同理由命题B为真可知a>c>b或b>a>c.
从而可知,b>a>c.
所以三个人年龄的大小顺序为b最大,a次之,c最小.【想一想】在四种命题中,真命题的个数可能有几种?
提示:因为原命题和逆否命题,逆命题和否命题互为逆否命题,它们同真同假,所以真命题的个数可能为0,2,4,共三种. 充分条件、必要条件和充要条件的判断及应用
【技法点拨】
1.判断充分条件、必要条件和充要条件的一点注意和四个方面
(1)因为条件对结论有四种关系,所以在判断时,一定要全面.
(2)充分条件、必要条件和充要条件的判断,实质是判断由条件和结论构成命题及其逆命题的真假. ①若原命题为真,逆命题为假,则条件是结论的充分但不必要条件;
②若逆命题为真,原命题为假,则条件是结论的必要但不充分条件;
③若原命题为真,逆命题也为真,则条件是结论的充要条件;
④若原命题为假,逆命题也为假,则条件是结论的既不充分也不必要条件.2.充分条件、必要条件和充要条件的应用
此类问题是指属于已知条件是结论的充分但不必要条件、必要但不充分条件或者充要条件,来求某个字母的值或范围.涉及到的数学知识主要是不等式问题,根据相应知识列不等式(组)求解.【典例2】(1)(2011·山东高考)对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的
( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件(2)已知全集U=R,非空集合A={ },B={x|
}.
①当a= 时,求( B)∩A;
②命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.【解析】(1)选B.“y=f(x)是奇函数”,图象关于原点对称,所以“y=|f(x)|的图象关于y轴对称”;
“y=|f(x)|的图象关于y轴对称”,y=f(x)的图象关于y轴对称或者关于原点对称,所以y=f(x)不一定为奇函数.(2)①当 时,
∴ B={x|x≤ 或x≥ }.
∴( B)∩A={x| ≤x< }.②∵a2+2>a,∴B={x|a(i)当3a+1>2,即a> 时,A={x|2∵q是p的必要条件,∴A?B.
∴(ii)当3a+1=2,即a= 时,A=?,不符合题意;
(iii)当3a+1<2,即a< 时,A={x|3a+1由A?B得
综上所述:a的取值范围为[ )∪( ].【总结】题(2)的解答用到的数学思想及应用此种思想需要注意的问题.
提示:题(2)的解答用到的思想方法是分类讨论思想. 应用此种思想方法需要注意以下三点:
(1)分类标准要唯一;
(2)分类要做到各类之间不重复;
(3)所有情况要找全. 命题“p∧q”、“p∨q”的真假判断
【技法点拨】
1.命题“p∧q”、“p∨q”的真假判断的三个过程
(1)首先将所给命题写为命题“p∧q”、“p∨q”.
(2)判断命题p与q的真假.
(3)由命题“p∧q”、“p∨q”真假的判断方法做出判断.
2.命题“p∧q”、“p∨q”真假的应用
此类问题是指由命题“p∧q”、“p∨q”的真假,判断命题p与q的真假,依次解决相关问题.【典例3】(1)给出两个命题:p:函数y=x2-x-1有两个不
同的零点;q:若 <1,则x>1,那么在下列四个命题中,真命
题是( )
(A)(﹁p)∨q (B)p∧q
(C)(﹁p)∧(﹁q) (D)(﹁p)∨(﹁q)
(2)已知命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个
不同的交点;命题q:方程4x2+4(m-2)x+1=0无实根.若“p或q”
为真,“p且q”为假,求实数m的取值范围.【解析】(1)选D.对于p,函数对应的方程x2-x-1=0的判别式Δ=(-1)2-4×(-1)=5>0.
可知函数有两个不同的零点,故p为真.
当x<0时,不等式 <1恒成立;
当x>0时,不等式的解为x>1.
故不等式 <1的解为x<0或x>1.
故命题q为假命题.
所以只有( p)∨( q)为真.(2)因为命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个
不同的交点,所以
∴m>2.因为命题q:方程4x2+4(m-2)x+1=0无实根,所以q:Δ=16(m-2)2-16=16(m2-4m+3)<0,
∴1∵p或q为真,p且q为假,∴p真q假或p假q真.
∴【想一想】在解题(2)时,对于条件是怎样处理的?从中你又得到怎样的启示?
提示:在解题(2)时,首先将条件化简,找到与之等价的结论. 从中得到的启示是:当题目的条件所反映的关系不直接时,应先将其化简找到它的等价条件,然后再求解. 含有一个量词的命题的否定
【技法点拨】
1.全称命题与特称命题真假的判断方法
(1)判断全称命题为真命题,需严格的逻辑推理证明,判断全称命题为假命题,只需举出反例.(2)判断特称命题为真命题,需要举出正例,而判断特称命题为假命题时,要有严格的逻辑证明.
2.含有一个量词的命题否定的关注点
全称命题的否定是特称命题,特称命题的否定是全称命题.否定时既要改写量词,又要否定结论.【典例4】已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx;
(1)若“存在实数x0,使得f(x0)≤0”是假命题,求实数m的取值范围;
(2)是否存在实数m,使得:对任意实数x,f(x)与g(x)至少有一个为正数?若存在,求m的取值范围;若不存在,请说明理由.【解析】(1)因为“存在实数x0,使得f(x0)≤0”是假命题,所以“对于任意实数x,使得f(x)>0”是真命题,即对于任意实数x,f(x)>0恒成立.
①当m=0时,不成立;
②当m>0时Δ=4(4-m)2-8m<0,∴2当m>0时,则只要f(x)>0在(-∞,0)上恒成立.
∴0【解析】①当m=0时,f(x)=-8x+1,满足要求;
②当m<0时,满足要求;
③当m>0时,只要Δ=4(4-m)2-8m≥0,即m≤2或m≥8,就成立.
综上所述,实数m的取值范围是m≤2或m≥8.【思考】题(1)解法的依据是什么?从中你又得到怎样的启示?
提示:题(1)解法的依据是命题“p与 p真假性相反”,从中得到的启示是:当一个问题从正面入手比较困难时,可以从问题的反面入手来解决,即“正难则反”.1.下列四个命题中,真命题个数是( )
①若“x+y=0,则x,y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1,则x2+2x+q=0有实根”的命题
④“等边三角形的三个内角相等”的逆否命题
(A)1 (B)2 (C)3 (D)4【解析】选C.①:命题“若x+y=0,则x,y互为相反数”的逆命题是“若x,y互为相反数,则x+y=0”,是真命题;②:命题“全等三角形的面积相等”的否命题是“若两个三角形不全等,则这两个三角形的面积不相等”,是假命题;③:因为q≤1,所以-q≥-1,即4-4q≥0,所以方程x2+2x+q=0有实根,是真命题;④:因为命题“等边三角形的三个内角相等”是真命题,所以它的逆否命题也是真命题.2.命题p:“对任意一个实数x,均有x2≥0”,则p为( )
(A)存在x0∈R,使得 ≤0
(B)对任意x∈R,均有x2≤0
(C)存在x0∈R,使得 <0
(D)对任意x∈R,均有x2<0
【解析】选C.因为命题p:“对任意一个实数x,均有x2≥0”是全称命题,所以它的否定是“存在x0∈R,使得 <0”.3.命题p:若x<-5,则x2+6x+5>0的否命题是________.
【解析】由否命题的定义知,命题p:若x<-5,则x2+6x+5>0的否命题是“若x≥-5,则x2+6x+5≤0”.
答案:若x≥-5,则x2+6x+5≤04.已知A和B是两个命题,如果A是B的充分条件,那么 A是 B
的________条件.
【解析】因为“A是B的充分条件”,即命题“若 A,则 B”
是真命题,由此知它的逆否命题“若 B,则 A”也是真命
题,即A是B的必要条件.
答案:必要5.设p:实数x满足x2-4ax+3a2<0,其中a>0,
命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若 p是 q的充分不必要条件,求实数a的取值范围.【解析】(1)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
又a>0,所以a当a=1时,11由
即q为真时,实数x的取值范围是2若p∧q为真,则p真且q真,所以实数x的取值范围是2(2)﹁p是﹁q的充分不必要条件,即﹁p?﹁q,且﹁q ﹁p,
设A={x|﹁p},B={x|﹁q},则A B.
又A={x|﹁p}={x|x≤a或x≥3a},
B={x|﹁q}={x≤2或x>3},
则03,
所以实数a的取值范围是1
【技法点拨】
1.四种命题的写法
(1)对条件、结论不明显的命题,可以先将命题改写成“若p,则q”的形式后再进行转换.
(2)分清命题的条件和结论,然后进行互换和否定,即可得到原命题的逆命题、否命题和逆否命题.2.四种命题真假的判断方法
因为互为逆否命题的真假等价,所以判断四个命题的真假,只需判断原命题与逆命题(或否命题)的真假即可.【典例1】a,b,c为三个人,命题A:“如果b的年龄不是最大的,那么a的年龄最小”和命题B:“如果c的年龄不是最小的,那么a的年龄最大”都是真命题,则a,b,c的年龄的大小顺序是否能确定?请说明理由.
【解析】能确定.理由如下:
显然命题A和B的原命题的结论是矛盾的,因此应该从它的逆否命题来考虑.①由命题A为真可知,当b不是最大时,则a是最小的,即若c最大,则a最小,所以c>b>a;而它的逆否命题也为真,即“a不是最小,则b是最大”为真,所以b>a>c.总之由命题A为真可知:c>b>a或b>a>c.
②同理由命题B为真可知a>c>b或b>a>c.
从而可知,b>a>c.
所以三个人年龄的大小顺序为b最大,a次之,c最小.【想一想】在四种命题中,真命题的个数可能有几种?
提示:因为原命题和逆否命题,逆命题和否命题互为逆否命题,它们同真同假,所以真命题的个数可能为0,2,4,共三种. 充分条件、必要条件和充要条件的判断及应用
【技法点拨】
1.判断充分条件、必要条件和充要条件的一点注意和四个方面
(1)因为条件对结论有四种关系,所以在判断时,一定要全面.
(2)充分条件、必要条件和充要条件的判断,实质是判断由条件和结论构成命题及其逆命题的真假. ①若原命题为真,逆命题为假,则条件是结论的充分但不必要条件;
②若逆命题为真,原命题为假,则条件是结论的必要但不充分条件;
③若原命题为真,逆命题也为真,则条件是结论的充要条件;
④若原命题为假,逆命题也为假,则条件是结论的既不充分也不必要条件.2.充分条件、必要条件和充要条件的应用
此类问题是指属于已知条件是结论的充分但不必要条件、必要但不充分条件或者充要条件,来求某个字母的值或范围.涉及到的数学知识主要是不等式问题,根据相应知识列不等式(组)求解.【典例2】(1)(2011·山东高考)对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的
( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件(2)已知全集U=R,非空集合A={ },B={x|
}.
①当a= 时,求( B)∩A;
②命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.【解析】(1)选B.“y=f(x)是奇函数”,图象关于原点对称,所以“y=|f(x)|的图象关于y轴对称”;
“y=|f(x)|的图象关于y轴对称”,y=f(x)的图象关于y轴对称或者关于原点对称,所以y=f(x)不一定为奇函数.(2)①当 时,
∴ B={x|x≤ 或x≥ }.
∴( B)∩A={x| ≤x< }.②∵a2+2>a,∴B={x|a
∴(ii)当3a+1=2,即a= 时,A=?,不符合题意;
(iii)当3a+1<2,即a< 时,A={x|3a+1
综上所述:a的取值范围为[ )∪( ].【总结】题(2)的解答用到的数学思想及应用此种思想需要注意的问题.
提示:题(2)的解答用到的思想方法是分类讨论思想. 应用此种思想方法需要注意以下三点:
(1)分类标准要唯一;
(2)分类要做到各类之间不重复;
(3)所有情况要找全. 命题“p∧q”、“p∨q”的真假判断
【技法点拨】
1.命题“p∧q”、“p∨q”的真假判断的三个过程
(1)首先将所给命题写为命题“p∧q”、“p∨q”.
(2)判断命题p与q的真假.
(3)由命题“p∧q”、“p∨q”真假的判断方法做出判断.
2.命题“p∧q”、“p∨q”真假的应用
此类问题是指由命题“p∧q”、“p∨q”的真假,判断命题p与q的真假,依次解决相关问题.【典例3】(1)给出两个命题:p:函数y=x2-x-1有两个不
同的零点;q:若 <1,则x>1,那么在下列四个命题中,真命
题是( )
(A)(﹁p)∨q (B)p∧q
(C)(﹁p)∧(﹁q) (D)(﹁p)∨(﹁q)
(2)已知命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个
不同的交点;命题q:方程4x2+4(m-2)x+1=0无实根.若“p或q”
为真,“p且q”为假,求实数m的取值范围.【解析】(1)选D.对于p,函数对应的方程x2-x-1=0的判别式Δ=(-1)2-4×(-1)=5>0.
可知函数有两个不同的零点,故p为真.
当x<0时,不等式 <1恒成立;
当x>0时,不等式的解为x>1.
故不等式 <1的解为x<0或x>1.
故命题q为假命题.
所以只有( p)∨( q)为真.(2)因为命题p:函数f(x)=x2+mx+1的图象与x轴负半轴有两个
不同的交点,所以
∴m>2.因为命题q:方程4x2+4(m-2)x+1=0无实根,所以q:Δ=16(m-2)2-16=16(m2-4m+3)<0,
∴1
∴【想一想】在解题(2)时,对于条件是怎样处理的?从中你又得到怎样的启示?
提示:在解题(2)时,首先将条件化简,找到与之等价的结论. 从中得到的启示是:当题目的条件所反映的关系不直接时,应先将其化简找到它的等价条件,然后再求解. 含有一个量词的命题的否定
【技法点拨】
1.全称命题与特称命题真假的判断方法
(1)判断全称命题为真命题,需严格的逻辑推理证明,判断全称命题为假命题,只需举出反例.(2)判断特称命题为真命题,需要举出正例,而判断特称命题为假命题时,要有严格的逻辑证明.
2.含有一个量词的命题否定的关注点
全称命题的否定是特称命题,特称命题的否定是全称命题.否定时既要改写量词,又要否定结论.【典例4】已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx;
(1)若“存在实数x0,使得f(x0)≤0”是假命题,求实数m的取值范围;
(2)是否存在实数m,使得:对任意实数x,f(x)与g(x)至少有一个为正数?若存在,求m的取值范围;若不存在,请说明理由.【解析】(1)因为“存在实数x0,使得f(x0)≤0”是假命题,所以“对于任意实数x,使得f(x)>0”是真命题,即对于任意实数x,f(x)>0恒成立.
①当m=0时,不成立;
②当m>0时Δ=4(4-m)2-8m<0,∴2
∴0
②当m<0时,满足要求;
③当m>0时,只要Δ=4(4-m)2-8m≥0,即m≤2或m≥8,就成立.
综上所述,实数m的取值范围是m≤2或m≥8.【思考】题(1)解法的依据是什么?从中你又得到怎样的启示?
提示:题(1)解法的依据是命题“p与 p真假性相反”,从中得到的启示是:当一个问题从正面入手比较困难时,可以从问题的反面入手来解决,即“正难则反”.1.下列四个命题中,真命题个数是( )
①若“x+y=0,则x,y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1,则x2+2x+q=0有实根”的命题
④“等边三角形的三个内角相等”的逆否命题
(A)1 (B)2 (C)3 (D)4【解析】选C.①:命题“若x+y=0,则x,y互为相反数”的逆命题是“若x,y互为相反数,则x+y=0”,是真命题;②:命题“全等三角形的面积相等”的否命题是“若两个三角形不全等,则这两个三角形的面积不相等”,是假命题;③:因为q≤1,所以-q≥-1,即4-4q≥0,所以方程x2+2x+q=0有实根,是真命题;④:因为命题“等边三角形的三个内角相等”是真命题,所以它的逆否命题也是真命题.2.命题p:“对任意一个实数x,均有x2≥0”,则p为( )
(A)存在x0∈R,使得 ≤0
(B)对任意x∈R,均有x2≤0
(C)存在x0∈R,使得 <0
(D)对任意x∈R,均有x2<0
【解析】选C.因为命题p:“对任意一个实数x,均有x2≥0”是全称命题,所以它的否定是“存在x0∈R,使得 <0”.3.命题p:若x<-5,则x2+6x+5>0的否命题是________.
【解析】由否命题的定义知,命题p:若x<-5,则x2+6x+5>0的否命题是“若x≥-5,则x2+6x+5≤0”.
答案:若x≥-5,则x2+6x+5≤04.已知A和B是两个命题,如果A是B的充分条件,那么 A是 B
的________条件.
【解析】因为“A是B的充分条件”,即命题“若 A,则 B”
是真命题,由此知它的逆否命题“若 B,则 A”也是真命
题,即A是B的必要条件.
答案:必要5.设p:实数x满足x2-4ax+3a2<0,其中a>0,
命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若 p是 q的充分不必要条件,求实数a的取值范围.【解析】(1)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
又a>0,所以a
即q为真时,实数x的取值范围是2
设A={x|﹁p},B={x|﹁q},则A B.
又A={x|﹁p}={x|x≤a或x≥3a},
B={x|﹁q}={x≤2或x>3},
则0
所以实数a的取值范围是1
