数学苏教版选修1-1课件: 2.2.2 椭圆的几何性质 课件(19张)
文档属性
| 名称 | 数学苏教版选修1-1课件: 2.2.2 椭圆的几何性质 课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 243.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 00:00:00 | ||
图片预览






文档简介
课件19张PPT。A级问题1.椭圆的定义:平面内到两个定点F1、F2的距离和等于常数(大于F1F2 )的点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2温故而知新焦点在x轴上焦点在y轴上椭圆的几何性质4.本节课将从哪几个方面研究椭圆的几何性质?
A级问题分层次问题学习椭圆的范围 椭圆的对称性
椭圆的顶点 椭圆的离心率5.我们是如何探索椭圆范围的? 椭圆的范围具有什么特点? oxy由即说明:
椭圆位于矩形之中。同理可得分层次问题学习B级问题6.椭圆对称性探究把 换成 ,方程不变说明:
椭圆关于---轴对称;
椭圆关于---轴对称;
椭圆关于---点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心
小结:将对称问题转化为点的对称分层次问题学习B级问题7.椭圆顶点概念在椭圆令 x=0,得 y=?,
说明椭圆与 y轴的交点为______
令 y=0,得 x=?,说明椭圆与 x轴的交点为______顶点:
长轴:
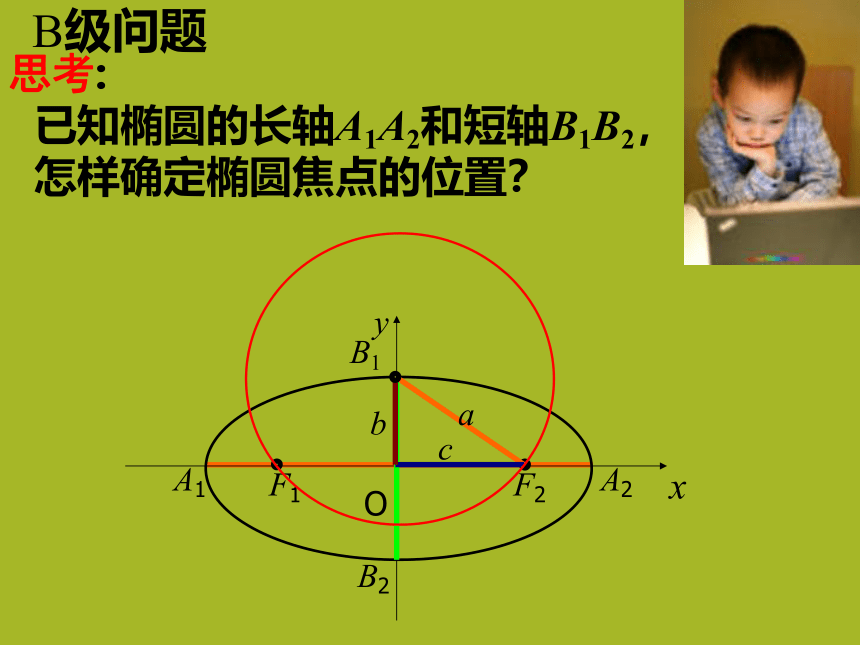
短轴:oxy中,a、b分别叫做椭圆的__________和________。线段A1A2叫做椭圆的长轴线段B1B2叫做椭圆的短轴椭圆与它的对称轴的四个交点,叫做椭圆的顶点。A级问题分层次问题学习O x F1 A2B1 B2 y A1a c b F2 B级问题思考: 已知椭圆的长轴A1A2和短轴B1B2, 怎样确定椭圆焦点的位置?四、椭圆的离心率分层次问题学习(A级问题)8.椭圆的离心率是如何定义的?记为e(C级问题)9.请谈谈你对椭圆离心率e的认识?a.离心率是刻画椭圆什么性质的量?
b.离心率与椭圆的大小有关吗?
c.椭圆中的参数a、b、c变化时对离心率e 有何影响?
d.椭圆的离心率有范围吗?在其范围内椭圆如何变化?
e.能只用椭圆中的参数a、b来刻画离心率吗?
椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率.[1]离心率的取值范围:[2]离心率对椭圆形状的影响:02)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆例1已知椭圆方程为16x2+25y2=400, 它的长轴长是: .短轴长是: .
焦距是: . 离心率等于: .
焦点坐标是: .顶点坐标是: .
外切矩形的面积等于: . 108680解题的关键:1、将椭圆方程转化为标准方程 明确a、b2、确定焦点的位置分层次问题检测A级问题根据所学知识画椭圆简图A1 B1 A2 B2 2.已知椭圆中心在原点,对称轴为坐标轴, 焦点在y轴上,长轴是短轴的2倍,焦距为2, 求椭圆的方程。B级问题分层次问题检测|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称长半轴长为a,短半轴长为b.焦距为2ca2=b2+c2小结:基本元素1.基本量:a、b、c、e2.基本点:顶点、焦点、中心(共七个点)3.基本线:对称轴2.已知椭圆的方程为x2+a2y2=a(a>0且a 1)它的长轴长是: ;
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ;
顶点坐标是: ;
外切矩形的面积等于: ; 当a>1时:
。
。
。
。
。
。
。
当0焦距是: .离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 2练习1.练习2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .敬请各位老师
批评指正!备用练习
1.椭圆过 点,离心率为 ,求椭圆的标准方程.
2.如图, , 求椭圆标准方程.
A级问题分层次问题学习椭圆的范围 椭圆的对称性
椭圆的顶点 椭圆的离心率5.我们是如何探索椭圆范围的? 椭圆的范围具有什么特点? oxy由即说明:
椭圆位于矩形之中。同理可得分层次问题学习B级问题6.椭圆对称性探究把 换成 ,方程不变说明:
椭圆关于---轴对称;
椭圆关于---轴对称;
椭圆关于---点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心
小结:将对称问题转化为点的对称分层次问题学习B级问题7.椭圆顶点概念在椭圆令 x=0,得 y=?,
说明椭圆与 y轴的交点为______
令 y=0,得 x=?,说明椭圆与 x轴的交点为______顶点:
长轴:
短轴:oxy中,a、b分别叫做椭圆的__________和________。线段A1A2叫做椭圆的长轴线段B1B2叫做椭圆的短轴椭圆与它的对称轴的四个交点,叫做椭圆的顶点。A级问题分层次问题学习O x F1 A2B1 B2 y A1a c b F2 B级问题思考: 已知椭圆的长轴A1A2和短轴B1B2, 怎样确定椭圆焦点的位置?四、椭圆的离心率分层次问题学习(A级问题)8.椭圆的离心率是如何定义的?记为e(C级问题)9.请谈谈你对椭圆离心率e的认识?a.离心率是刻画椭圆什么性质的量?
b.离心率与椭圆的大小有关吗?
c.椭圆中的参数a、b、c变化时对离心率e 有何影响?
d.椭圆的离心率有范围吗?在其范围内椭圆如何变化?
e.能只用椭圆中的参数a、b来刻画离心率吗?
椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率.[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0
焦距是: . 离心率等于: .
焦点坐标是: .顶点坐标是: .
外切矩形的面积等于: . 108680解题的关键:1、将椭圆方程转化为标准方程 明确a、b2、确定焦点的位置分层次问题检测A级问题根据所学知识画椭圆简图A1 B1 A2 B2 2.已知椭圆中心在原点,对称轴为坐标轴, 焦点在y轴上,长轴是短轴的2倍,焦距为2, 求椭圆的方程。B级问题分层次问题检测|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称长半轴长为a,短半轴长为b.焦距为2ca2=b2+c2小结:基本元素1.基本量:a、b、c、e2.基本点:顶点、焦点、中心(共七个点)3.基本线:对称轴2.已知椭圆的方程为x2+a2y2=a(a>0且a 1)它的长轴长是: ;
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ;
顶点坐标是: ;
外切矩形的面积等于: ; 当a>1时:
。
。
。
。
。
。
。
当0
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 2练习1.练习2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .敬请各位老师
批评指正!备用练习
1.椭圆过 点,离心率为 ,求椭圆的标准方程.
2.如图, , 求椭圆标准方程.
