第二章 相交线与平行线复习题---填空题(含解析)
文档属性
| 名称 | 第二章 相交线与平行线复习题---填空题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 10:29:02 | ||
图片预览




文档简介
北师大版数学七下第二章相交线与平行线复习题---填空题
一.填空题
1.(2018秋?龙岩期末)如图,直线AB,CD交于点O,我们知道∠1=∠2,那么其理由是 .
2.(2018秋?长春期末)如图,直线AB、CD相交于点O.若∠1+∠2=100°,则∠BOC的大小为 度.
3.(2018秋?香坊区期末)如图,直线AB、CD相交于点O,OE⊥CD,垂足为O,若射线OF在∠AOE的内部,∠EOF=25°,∠AOF=∠BOD,则∠BOC= °.
4.(2018秋?二道区期末)直线AB与射线OC相交于点O,OC⊥OD于O,若∠AOC=60°,则∠BOD= 度.
5.(2018春?容县期中)在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则 .
6.(2018春?江油市期末)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60°,则这两个角的度数分别为 .
7.(2018秋?平谷区期末)如图,直线AB表示某天然气的主管道,现在要从主管道引一条分管道到某村庄P,则沿图中线段 修建可使用料最省.理由是 .
8.(2018春?蔡甸区期末)在△ABC中∠B=90°,BC=5,AB=12,AC=13,则点B到斜边AC的距离是 .
9.(2018春?徐州期末)在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
10.(2018春?罗山县期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
11.(2018春?杭州期中)两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
12.(2018?湘潭)如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
13.(2017秋?孟津县期末)如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
14.(2018春?石景山区期末)如图,若满足条件 ,则有AB∥CD,理由是 .(要求:不再添加辅助线,只需填一个答案即可)
15.(2018春?永新县期末)如图∠2=∠3,∠1=60°,要使a∥b,则∠4= .
16.(2018?岳池县模拟)如图,∠1=∠2,需增加条件 可以使得AB∥CD(只写一种).
17.(2018春?琼中县期中)如图所示,点D、E、F分别是AB、BC、AC上的点,
(1)若∠2= ,则DE∥AC;
(2)若∠2= ,则DF∥BC.
18.(2018?本溪)如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为 .
19.(2018?辽阳)将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2= .
20.(2018?广元)如图,∠A=22°,∠E=30°,AC∥EF,则∠1的度数为 .
21.(2018?青海)如图,直线AB∥CD,直线EF与AB、CD相交于点E、F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= .
22.(2018?南通)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE= 度.
23.(2018?铜仁市)如图,m∥n,∠1=110°,∠2=100°,则∠3= °.
24.(2018?苏州)如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 °.
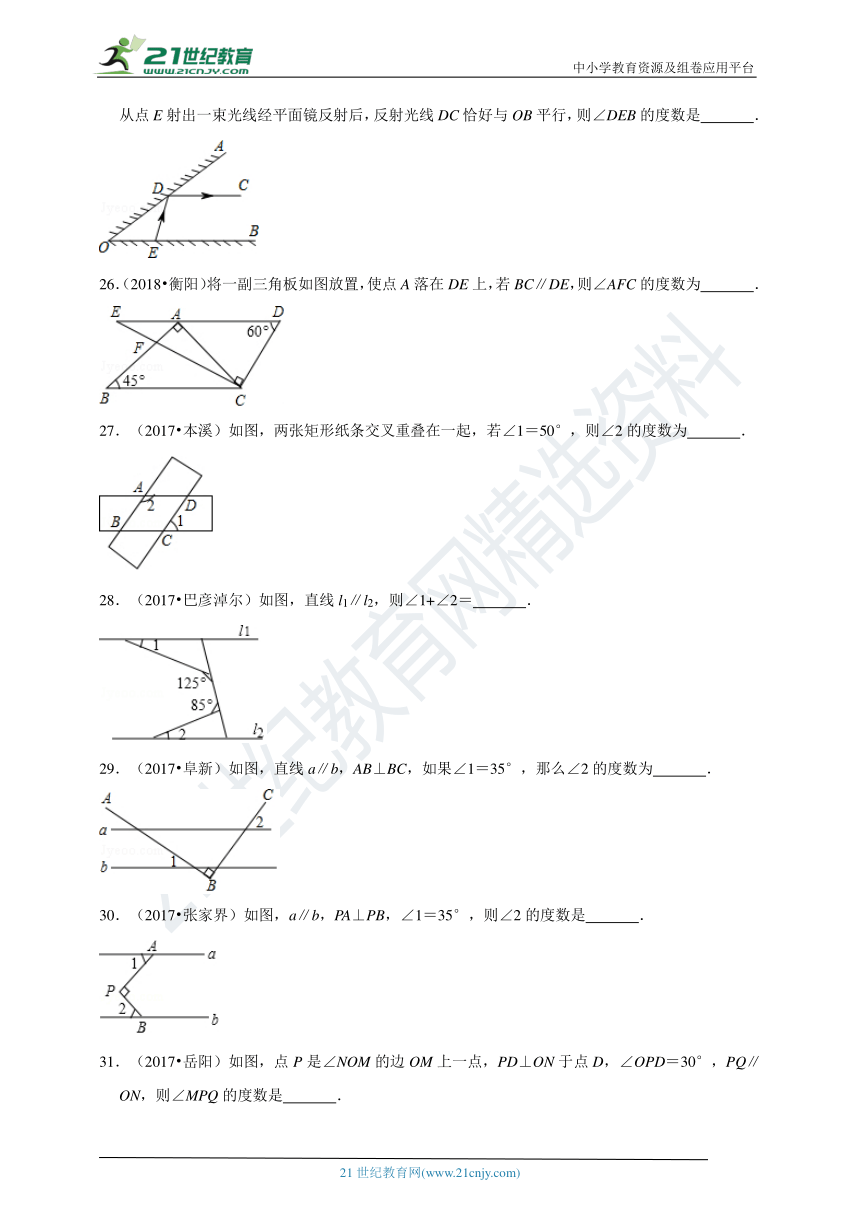
25.(2018?通辽)如图,∠AOB的一边OA为平面镜,∠AOB=37°45′,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
26.(2018?衡阳)将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 .
27.(2017?本溪)如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 .
28.(2017?巴彦淖尔)如图,直线l1∥l2,则∠1+∠2= .
29.(2017?阜新)如图,直线a∥b,AB⊥BC,如果∠1=35°,那么∠2的度数为 .
30.(2017?张家界)如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
31.(2017?岳阳)如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
32.(2017?金华)如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= .
33.(2016?镇江)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °.
北师大版数学七下第二章相交线与平行线复习题---填空题
参考答案与试题解析
一.填空题
1.(2018秋?龙岩期末)如图,直线AB,CD交于点O,我们知道∠1=∠2,那么其理由是 同角的补角相等 .
【分析】依据∠1+∠3=180°,∠2+∠3=180°,即可得到∠1=∠2,依据为同角的补角相等.
【解答】解:∵直线AB,CD交于点O,
∴∠1+∠3=180°,∠2+∠3=180°,
∴∠1=∠2(同角的补角相等),
故答案为:同角的补角相等.
2.(2018秋?长春期末)如图,直线AB、CD相交于点O.若∠1+∠2=100°,则∠BOC的大小为 130 度.
【分析】两直线相交,对顶角相等,即∠1=∠2,已知∠1+∠2=100°,可求∠1;又∠1与∠BOC互为邻补角,即∠1+∠BOC=180°,将∠1的度数代入,可求∠BOC.
【解答】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠1+∠2=100°,
∴∠1=50°.
∵∠1与∠BOC互为邻补角,
∴∠BOC=180°﹣∠1=180°﹣50°=130°.
故答案为:130.
3.(2018秋?香坊区期末)如图,直线AB、CD相交于点O,OE⊥CD,垂足为O,若射线OF在∠AOE的内部,∠EOF=25°,∠AOF=∠BOD,则∠BOC= 141 °.
【分析】直接利用已知设∠AOF=2x,则∠BOD=3x,进而利用垂直的定义得出∠AOF+∠BOD,进而得出答案.
【解答】解:∵∠AOF=∠BOD,
∴设∠AOF=2x,则∠BOD=3x,
∵OE⊥CD,∠EOF=25°,
∴∠AOF+∠BOD=90°﹣25°=65°,
∴2x+3x=65°,
解得:x=13°,
∴∠AOF=26°,
∴∠BOC=∠AOD=90°+26°+25°=141°.
故答案为:141.
4.(2018秋?二道区期末)直线AB与射线OC相交于点O,OC⊥OD于O,若∠AOC=60°,则∠BOD= 30或150 度.
【分析】根据题意画出图形,由OC⊥OD,∠AOC=60°,利用垂直的定义易得∠AOD,再利用补角的定义可得结果.
【解答】解:根据题意画图如下,
情况一:如图1,
∵OC⊥OD,∠AOC=60°,
∴∠AOD=∠COD﹣∠AOC=90﹣60°=30°,
∴∠COD=180°﹣∠AOD=180°﹣30°=150°;
情况二:如图2,
∵OC⊥OD,∠AOC=60°,
∴∠AOD=∠COD+∠AOC=90°+60°=150°,
∴∠COD=180°﹣∠AOD=180°﹣150°=30°,
故答案为:150或30.
5.(2018春?容县期中)在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则 a∥b .
【分析】根据平行线的判定解答即可.
【解答】解:在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则a∥b,
故答案为:a∥b.
6.(2018春?江油市期末)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60°,则这两个角的度数分别为 48°、132°或20°、20°. .
【分析】分两种情况进行讨论,依据两个角的两条边分别垂直画出图形,而其中一个角比另一个角的4倍少60°,即可得到这两个角的度数.
【解答】解:如图,α+β=180°,β=4α﹣60°,
解得α=48°,β=132°;
如图,α=β,β=4α﹣60°,
解得α=β=20°;
综上所述,这两个角的度数分别为48°、132°或20°、20°.
故答案为:48°、132°或20°、20°.
7.(2018秋?平谷区期末)如图,直线AB表示某天然气的主管道,现在要从主管道引一条分管道到某村庄P,则沿图中线段 PD 修建可使用料最省.理由是 垂线段最短 .
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短,根据垂线段最短即可得出结论.
【解答】解:由图可得,PD<PC<PE,
∴沿图中线段PD修建可使用料最省,理由是垂线段最短,
故答案为:PD,垂线段最短.
8.(2018春?蔡甸区期末)在△ABC中∠B=90°,BC=5,AB=12,AC=13,则点B到斜边AC的距离是 .
【分析】设AC边上的高为h,再根据三角形的面积公式即可得出结论.
【解答】解:设AC边上的高为h,
∵在Rt△ABC中,∠B=90°,AB=5,BC=12,AC=13,
∴AB?BC=AC?h,
∴h===.
故答案为:.
9.(2018春?徐州期末)在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 a∥c .
【分析】根据在同一平面内,垂直于同一条直线的两条直线互相垂直即可求解.
【解答】解:∵a⊥b,b⊥c,
∴a∥c.
故答案为a∥c.
10.(2018春?罗山县期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 ①② (填序号).
【分析】准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解答】解:①∠A与∠1是同位角,此结论正确;
②∠A与∠B是同旁内角,此结论正确;
③∠4与∠1不是内错角,此结论错误;
④∠1与∠3是内错角,此结论错误;
故答案为:①②.
11.(2018春?杭州期中)两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 20° .
【分析】设∠1=x°,则∠3=2x°,∠2=8x°,根据邻补角互补可得方程,求解即可.
【解答】解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180,
解得:x=20°,
∴∠1=20°.
故答案为:20°.
12.(2018?湘潭)如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 ∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE .(任意添加一个符合题意的条件即可)
【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断.
【解答】解:若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为:∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
13.(2017秋?孟津县期末)如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 10° .
【分析】根据平行线的性质,求得∠AOD′的度数,即可确定旋转的角度,即∠DOD′的大小.
【解答】解:∵OD′∥AC,
∴∠AOD′=180°﹣∠A=110°,
∴∠DOD′=∠AOD′﹣∠AOD=110°﹣100°=10°.
故答案为:10°.
14.(2018春?石景山区期末)如图,若满足条件 ∠A=∠3 ,则有AB∥CD,理由是 同位角相等,两直线平行 .(要求:不再添加辅助线,只需填一个答案即可)
【分析】依据平行线的判定进行添加即可,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
【解答】解:若∠A=∠3,则同位角相等,两直线平行,
故答案为:∠A=∠3,同位角相等,两直线平行.(答案不唯一)
15.(2018春?永新县期末)如图∠2=∠3,∠1=60°,要使a∥b,则∠4= 120° .
【分析】延长AE交直线b于B,依据∠2=∠3,可得AE∥CD,当a∥b时,可得∠1=∠5=60°,依据平行线的性质,即可得到∠4的度数.
【解答】解:如图,延长AE交直线b于B,
∵∠2=∠3,
∴AE∥CD,
当a∥b时,∠1=∠5=60°,
∴∠4=180°﹣∠5=180°﹣60°=120°,
故答案为:120°.
16.(2018?岳池县模拟)如图,∠1=∠2,需增加条件 ∠FAD=∠EDA(或AF∥DE) 可以使得AB∥CD(只写一种).
【分析】两条直线被第三条所截,如果内错角相等,那么这两条直线平行,据此可得添加的条件.
【解答】解:当∠FAD=∠EDA时,
∵∠1=∠2,
∴∠BAD=∠CDA,
∴AB∥CD;
当AF∥DE时,∠FAD=∠EDA,
同理可得AB∥CD.
故答案为:∠FAD=∠EDA(或AF∥DE)
17.(2018春?琼中县期中)如图所示,点D、E、F分别是AB、BC、AC上的点,
(1)若∠2= ∠1 ,则DE∥AC;
(2)若∠2= ∠DEB ,则DF∥BC.
【分析】根据平行线的判定定理:内错角相等,两直线平行,来填空.
【解答】解:(1)当∠2=∠1时,DE∥AC(内错角相等,两直线平行);
(2)当∠2=∠DEB时,DF∥BC(内错角相等,两直线平行).
故答案是:∠1;∠DEB.
18.(2018?本溪)如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为 54° .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,求出∠BCD,再根据两直线平行,内错角相等进行解答即可.
【解答】解:如图,∵∠E=34°,∠D=20°,
∴∠BCD=∠D+∠E=20°+34°=54°,
∵AB∥CD,
∴∠B=∠BCD=54°.
故答案为:54°.
19.(2018?辽阳)将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2= 126° .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3,再根据两直线平行,同位角相等可得∠2=∠3.
【解答】解:如图,由三角形的外角性质得,∠3=90°+∠1=90°+36°=126°,
∵纸条的两边互相平行,
∴∠2=∠3=126°.
故答案为:126°.
20.(2018?广元)如图,∠A=22°,∠E=30°,AC∥EF,则∠1的度数为 52° .
【分析】依据∠E=30°,AC∥EF,即可得到∠AGH=∠E=30°,再根据∠1是△AGH的外角,即可得出∠1=∠A+∠AGH=52°.
【解答】解:如图,∵∠E=30°,AC∥EF,
∴∠AGH=∠E=30°,
又∵∠1是△AGH的外角,
∴∠1=∠A+∠AGH=22°+30°=52°,
故答案为:52°.
21.(2018?青海)如图,直线AB∥CD,直线EF与AB、CD相交于点E、F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= 50° .
【分析】先根据平行线的性质求出∠BEN的度数,再由角平分线的定义得出∠BEF的度数,根据平行线的性质即可得出∠2的度数.
【解答】解:∵AB∥CD,∠1=65°,
∴∠BEN=∠1=65°.
∵EN平分∠BEF,
∴∠BEF=2∠BEN=130°,
∴∠2=180°﹣∠BEF=180°﹣130°=50°.
故答案为:50°.
22.(2018?南通)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE= 130 度.
【分析】依据∠AOB=40°,OP平分∠AOB,可得∠AOC=∠BOC=20°,再根据CD⊥OA于点D,CE∥OB,即可得出∠DCP=90°+20°=110°,∠PCE=∠POB=20°,依据∠DCE=∠DCP+∠PCE进行计算即可.
【解答】解:∵∠AOB=40°,OP平分∠AOB,
∴∠AOC=∠BOC=20°,
又∵CD⊥OA于点D,CE∥OB,
∴∠DCP=90°+20°=110°,∠PCE=∠POB=20°,
∴∠DCE=∠DCP+∠PCE=110°+20°=130°,
故答案为:130.
23.(2018?铜仁市)如图,m∥n,∠1=110°,∠2=100°,则∠3= 150 °.
【分析】两直线平行,同旁内角互补,然后根据三角形内角和为180°即可解答.
【解答】解:如图,
∵m∥n,∠1=110°,
∴∠4=70°,
∵∠2=100°,
∴∠5=80°,
∴∠6=180°﹣∠4﹣∠5=30°,
∴∠3=180°﹣∠6=150°,
故答案为:150.
24.(2018?苏州)如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 80 °.
【分析】依据DE∥AF,可得∠BED=∠BFA,再根据三角形外角性质,即可得到∠BFA=20°+60°=80°,进而得出∠BED=80°.
【解答】解:如图所示,∵DE∥AF,
∴∠BED=∠BFA,
又∵∠CAF=20°,∠C=60°,
∴∠BFA=20°+60°=80°,
∴∠BED=80°,
故答案为:80.
25.(2018?通辽)如图,∠AOB的一边OA为平面镜,∠AOB=37°45′,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 75°30′(或75.5°) .
【分析】首先证明∠EDO=∠AOB=37°45′,根据∠DEB=∠AOB+∠EDO计算即可解决问题;
【解答】解:∵CD∥OB,
∴∠ADC=∠AOB,
∵∠EDO=∠CDA,
∴∠EDO=∠AOB=37°45′,
∴∠DEB=∠AOB+∠EDO=2×37°45′=75°30′(或75.5°),
故答案为75°30′(或75.5°).
26.(2018?衡阳)将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 75° .
【分析】先根据BC∥DE及三角板的度数求出∠EAB的度数,再根据三角形内角与外角的性质即可求出∠AFC的度数.
【解答】解:∵BC∥DE,△ABC为等腰直角三角形,
∴∠FBC=∠EAB=(180°﹣90°)=45°,
∵∠AFC是△AEF的外角,
∴∠AFC=∠FAE+∠E=45°+30°=75°.
故答案为:75°.
27.(2017?本溪)如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 130° .
【分析】依据平行线的性质,即可得到∠ABC以及∠2的度数.
【解答】解:∵AD∥BC,AB∥CD,
∴∠1=∠ABC=50°,
∴∠2=180°﹣∠ABC=180°﹣50°=130°,
故答案为:130°.
28.(2017?巴彦淖尔)如图,直线l1∥l2,则∠1+∠2= 30° .
【分析】先利用三角形外角性质得∠1+∠3=125°,∠2+∠4=85°,把两式相加得到∠1+∠3+∠2+∠4=210°,再根据平行线的性质,由l1∥l2得到∠3+∠4=180°,然后通过角度的计算得到∠1+∠2的度数.
【解答】解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为:30°.
29.(2017?阜新)如图,直线a∥b,AB⊥BC,如果∠1=35°,那么∠2的度数为 55° .
【分析】平行线的性质即可得出∠BDE的度数,由垂线的性质和对顶角的定义即可得到求出∠2的度数.
【解答】解:如图,∵a∥b,
∴∠BDE=∠1=35°,
∵AB⊥BC,
∴Rt△BDE中,∠BED=90°﹣35°=55°,
∴∠2=∠BED=55°,
故答案为:55°.
30.(2017?张家界)如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 55° .
【分析】先延长AP交直线b于C,再根据平行线的性质以及三角形的外角性质进行计算即可.
【解答】解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
31.(2017?岳阳)如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 60° .
【分析】根据PQ∥ON,即可得到∠QPD=∠PDO=90°,再根据平角的定义,即可得到∠MPQ.
【解答】解:∵PD⊥ON于点D,
∴∠PDO=90°,
又∵PQ∥ON,
∴∠QPD=∠PDO=90°,
∵∠OPD=30°,
∴∠MPQ=180°﹣∠QPD﹣∠OPD=180°﹣90°﹣30°=60°.
故答案为:60°.
32.(2017?金华)如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= 20° .
【分析】先根据平行线的性质,得到∠BDC=50°,再根据∠ADB=30°,即可得出∠2=20°.
【解答】解:∵∠1=130°,
∴∠3=50°,
又∵l1∥l2,
∴∠BDC=50°,
又∵∠ADB=30°,
∴∠2=20°,
故答案为:20°.
33.(2016?镇江)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= 70 °.
【分析】根据平角等于180°列式计算得到∠3,根据两直线平行,同位角相等可得∠3=∠2.
【解答】解:∵∠1=20°,
∴∠3=90°﹣∠1=70°,
∵直线a∥b,
∴∠2=∠3=70°,
故答案是:70.
一.填空题
1.(2018秋?龙岩期末)如图,直线AB,CD交于点O,我们知道∠1=∠2,那么其理由是 .
2.(2018秋?长春期末)如图,直线AB、CD相交于点O.若∠1+∠2=100°,则∠BOC的大小为 度.
3.(2018秋?香坊区期末)如图,直线AB、CD相交于点O,OE⊥CD,垂足为O,若射线OF在∠AOE的内部,∠EOF=25°,∠AOF=∠BOD,则∠BOC= °.
4.(2018秋?二道区期末)直线AB与射线OC相交于点O,OC⊥OD于O,若∠AOC=60°,则∠BOD= 度.
5.(2018春?容县期中)在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则 .
6.(2018春?江油市期末)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60°,则这两个角的度数分别为 .
7.(2018秋?平谷区期末)如图,直线AB表示某天然气的主管道,现在要从主管道引一条分管道到某村庄P,则沿图中线段 修建可使用料最省.理由是 .
8.(2018春?蔡甸区期末)在△ABC中∠B=90°,BC=5,AB=12,AC=13,则点B到斜边AC的距离是 .
9.(2018春?徐州期末)在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
10.(2018春?罗山县期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
11.(2018春?杭州期中)两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
12.(2018?湘潭)如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
13.(2017秋?孟津县期末)如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
14.(2018春?石景山区期末)如图,若满足条件 ,则有AB∥CD,理由是 .(要求:不再添加辅助线,只需填一个答案即可)
15.(2018春?永新县期末)如图∠2=∠3,∠1=60°,要使a∥b,则∠4= .
16.(2018?岳池县模拟)如图,∠1=∠2,需增加条件 可以使得AB∥CD(只写一种).
17.(2018春?琼中县期中)如图所示,点D、E、F分别是AB、BC、AC上的点,
(1)若∠2= ,则DE∥AC;
(2)若∠2= ,则DF∥BC.
18.(2018?本溪)如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为 .
19.(2018?辽阳)将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2= .
20.(2018?广元)如图,∠A=22°,∠E=30°,AC∥EF,则∠1的度数为 .
21.(2018?青海)如图,直线AB∥CD,直线EF与AB、CD相交于点E、F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= .
22.(2018?南通)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE= 度.
23.(2018?铜仁市)如图,m∥n,∠1=110°,∠2=100°,则∠3= °.
24.(2018?苏州)如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 °.
25.(2018?通辽)如图,∠AOB的一边OA为平面镜,∠AOB=37°45′,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
26.(2018?衡阳)将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 .
27.(2017?本溪)如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 .
28.(2017?巴彦淖尔)如图,直线l1∥l2,则∠1+∠2= .
29.(2017?阜新)如图,直线a∥b,AB⊥BC,如果∠1=35°,那么∠2的度数为 .
30.(2017?张家界)如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
31.(2017?岳阳)如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
32.(2017?金华)如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= .
33.(2016?镇江)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °.
北师大版数学七下第二章相交线与平行线复习题---填空题
参考答案与试题解析
一.填空题
1.(2018秋?龙岩期末)如图,直线AB,CD交于点O,我们知道∠1=∠2,那么其理由是 同角的补角相等 .
【分析】依据∠1+∠3=180°,∠2+∠3=180°,即可得到∠1=∠2,依据为同角的补角相等.
【解答】解:∵直线AB,CD交于点O,
∴∠1+∠3=180°,∠2+∠3=180°,
∴∠1=∠2(同角的补角相等),
故答案为:同角的补角相等.
2.(2018秋?长春期末)如图,直线AB、CD相交于点O.若∠1+∠2=100°,则∠BOC的大小为 130 度.
【分析】两直线相交,对顶角相等,即∠1=∠2,已知∠1+∠2=100°,可求∠1;又∠1与∠BOC互为邻补角,即∠1+∠BOC=180°,将∠1的度数代入,可求∠BOC.
【解答】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠1+∠2=100°,
∴∠1=50°.
∵∠1与∠BOC互为邻补角,
∴∠BOC=180°﹣∠1=180°﹣50°=130°.
故答案为:130.
3.(2018秋?香坊区期末)如图,直线AB、CD相交于点O,OE⊥CD,垂足为O,若射线OF在∠AOE的内部,∠EOF=25°,∠AOF=∠BOD,则∠BOC= 141 °.
【分析】直接利用已知设∠AOF=2x,则∠BOD=3x,进而利用垂直的定义得出∠AOF+∠BOD,进而得出答案.
【解答】解:∵∠AOF=∠BOD,
∴设∠AOF=2x,则∠BOD=3x,
∵OE⊥CD,∠EOF=25°,
∴∠AOF+∠BOD=90°﹣25°=65°,
∴2x+3x=65°,
解得:x=13°,
∴∠AOF=26°,
∴∠BOC=∠AOD=90°+26°+25°=141°.
故答案为:141.
4.(2018秋?二道区期末)直线AB与射线OC相交于点O,OC⊥OD于O,若∠AOC=60°,则∠BOD= 30或150 度.
【分析】根据题意画出图形,由OC⊥OD,∠AOC=60°,利用垂直的定义易得∠AOD,再利用补角的定义可得结果.
【解答】解:根据题意画图如下,
情况一:如图1,
∵OC⊥OD,∠AOC=60°,
∴∠AOD=∠COD﹣∠AOC=90﹣60°=30°,
∴∠COD=180°﹣∠AOD=180°﹣30°=150°;
情况二:如图2,
∵OC⊥OD,∠AOC=60°,
∴∠AOD=∠COD+∠AOC=90°+60°=150°,
∴∠COD=180°﹣∠AOD=180°﹣150°=30°,
故答案为:150或30.
5.(2018春?容县期中)在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则 a∥b .
【分析】根据平行线的判定解答即可.
【解答】解:在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则a∥b,
故答案为:a∥b.
6.(2018春?江油市期末)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60°,则这两个角的度数分别为 48°、132°或20°、20°. .
【分析】分两种情况进行讨论,依据两个角的两条边分别垂直画出图形,而其中一个角比另一个角的4倍少60°,即可得到这两个角的度数.
【解答】解:如图,α+β=180°,β=4α﹣60°,
解得α=48°,β=132°;
如图,α=β,β=4α﹣60°,
解得α=β=20°;
综上所述,这两个角的度数分别为48°、132°或20°、20°.
故答案为:48°、132°或20°、20°.
7.(2018秋?平谷区期末)如图,直线AB表示某天然气的主管道,现在要从主管道引一条分管道到某村庄P,则沿图中线段 PD 修建可使用料最省.理由是 垂线段最短 .
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短,根据垂线段最短即可得出结论.
【解答】解:由图可得,PD<PC<PE,
∴沿图中线段PD修建可使用料最省,理由是垂线段最短,
故答案为:PD,垂线段最短.
8.(2018春?蔡甸区期末)在△ABC中∠B=90°,BC=5,AB=12,AC=13,则点B到斜边AC的距离是 .
【分析】设AC边上的高为h,再根据三角形的面积公式即可得出结论.
【解答】解:设AC边上的高为h,
∵在Rt△ABC中,∠B=90°,AB=5,BC=12,AC=13,
∴AB?BC=AC?h,
∴h===.
故答案为:.
9.(2018春?徐州期末)在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 a∥c .
【分析】根据在同一平面内,垂直于同一条直线的两条直线互相垂直即可求解.
【解答】解:∵a⊥b,b⊥c,
∴a∥c.
故答案为a∥c.
10.(2018春?罗山县期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 ①② (填序号).
【分析】准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解答】解:①∠A与∠1是同位角,此结论正确;
②∠A与∠B是同旁内角,此结论正确;
③∠4与∠1不是内错角,此结论错误;
④∠1与∠3是内错角,此结论错误;
故答案为:①②.
11.(2018春?杭州期中)两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 20° .
【分析】设∠1=x°,则∠3=2x°,∠2=8x°,根据邻补角互补可得方程,求解即可.
【解答】解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180,
解得:x=20°,
∴∠1=20°.
故答案为:20°.
12.(2018?湘潭)如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 ∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE .(任意添加一个符合题意的条件即可)
【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断.
【解答】解:若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为:∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
13.(2017秋?孟津县期末)如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 10° .
【分析】根据平行线的性质,求得∠AOD′的度数,即可确定旋转的角度,即∠DOD′的大小.
【解答】解:∵OD′∥AC,
∴∠AOD′=180°﹣∠A=110°,
∴∠DOD′=∠AOD′﹣∠AOD=110°﹣100°=10°.
故答案为:10°.
14.(2018春?石景山区期末)如图,若满足条件 ∠A=∠3 ,则有AB∥CD,理由是 同位角相等,两直线平行 .(要求:不再添加辅助线,只需填一个答案即可)
【分析】依据平行线的判定进行添加即可,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
【解答】解:若∠A=∠3,则同位角相等,两直线平行,
故答案为:∠A=∠3,同位角相等,两直线平行.(答案不唯一)
15.(2018春?永新县期末)如图∠2=∠3,∠1=60°,要使a∥b,则∠4= 120° .
【分析】延长AE交直线b于B,依据∠2=∠3,可得AE∥CD,当a∥b时,可得∠1=∠5=60°,依据平行线的性质,即可得到∠4的度数.
【解答】解:如图,延长AE交直线b于B,
∵∠2=∠3,
∴AE∥CD,
当a∥b时,∠1=∠5=60°,
∴∠4=180°﹣∠5=180°﹣60°=120°,
故答案为:120°.
16.(2018?岳池县模拟)如图,∠1=∠2,需增加条件 ∠FAD=∠EDA(或AF∥DE) 可以使得AB∥CD(只写一种).
【分析】两条直线被第三条所截,如果内错角相等,那么这两条直线平行,据此可得添加的条件.
【解答】解:当∠FAD=∠EDA时,
∵∠1=∠2,
∴∠BAD=∠CDA,
∴AB∥CD;
当AF∥DE时,∠FAD=∠EDA,
同理可得AB∥CD.
故答案为:∠FAD=∠EDA(或AF∥DE)
17.(2018春?琼中县期中)如图所示,点D、E、F分别是AB、BC、AC上的点,
(1)若∠2= ∠1 ,则DE∥AC;
(2)若∠2= ∠DEB ,则DF∥BC.
【分析】根据平行线的判定定理:内错角相等,两直线平行,来填空.
【解答】解:(1)当∠2=∠1时,DE∥AC(内错角相等,两直线平行);
(2)当∠2=∠DEB时,DF∥BC(内错角相等,两直线平行).
故答案是:∠1;∠DEB.
18.(2018?本溪)如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为 54° .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,求出∠BCD,再根据两直线平行,内错角相等进行解答即可.
【解答】解:如图,∵∠E=34°,∠D=20°,
∴∠BCD=∠D+∠E=20°+34°=54°,
∵AB∥CD,
∴∠B=∠BCD=54°.
故答案为:54°.
19.(2018?辽阳)将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2= 126° .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3,再根据两直线平行,同位角相等可得∠2=∠3.
【解答】解:如图,由三角形的外角性质得,∠3=90°+∠1=90°+36°=126°,
∵纸条的两边互相平行,
∴∠2=∠3=126°.
故答案为:126°.
20.(2018?广元)如图,∠A=22°,∠E=30°,AC∥EF,则∠1的度数为 52° .
【分析】依据∠E=30°,AC∥EF,即可得到∠AGH=∠E=30°,再根据∠1是△AGH的外角,即可得出∠1=∠A+∠AGH=52°.
【解答】解:如图,∵∠E=30°,AC∥EF,
∴∠AGH=∠E=30°,
又∵∠1是△AGH的外角,
∴∠1=∠A+∠AGH=22°+30°=52°,
故答案为:52°.
21.(2018?青海)如图,直线AB∥CD,直线EF与AB、CD相交于点E、F,∠BEF的平分线EN与CD相交于点N.若∠1=65°,则∠2= 50° .
【分析】先根据平行线的性质求出∠BEN的度数,再由角平分线的定义得出∠BEF的度数,根据平行线的性质即可得出∠2的度数.
【解答】解:∵AB∥CD,∠1=65°,
∴∠BEN=∠1=65°.
∵EN平分∠BEF,
∴∠BEF=2∠BEN=130°,
∴∠2=180°﹣∠BEF=180°﹣130°=50°.
故答案为:50°.
22.(2018?南通)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE= 130 度.
【分析】依据∠AOB=40°,OP平分∠AOB,可得∠AOC=∠BOC=20°,再根据CD⊥OA于点D,CE∥OB,即可得出∠DCP=90°+20°=110°,∠PCE=∠POB=20°,依据∠DCE=∠DCP+∠PCE进行计算即可.
【解答】解:∵∠AOB=40°,OP平分∠AOB,
∴∠AOC=∠BOC=20°,
又∵CD⊥OA于点D,CE∥OB,
∴∠DCP=90°+20°=110°,∠PCE=∠POB=20°,
∴∠DCE=∠DCP+∠PCE=110°+20°=130°,
故答案为:130.
23.(2018?铜仁市)如图,m∥n,∠1=110°,∠2=100°,则∠3= 150 °.
【分析】两直线平行,同旁内角互补,然后根据三角形内角和为180°即可解答.
【解答】解:如图,
∵m∥n,∠1=110°,
∴∠4=70°,
∵∠2=100°,
∴∠5=80°,
∴∠6=180°﹣∠4﹣∠5=30°,
∴∠3=180°﹣∠6=150°,
故答案为:150.
24.(2018?苏州)如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 80 °.
【分析】依据DE∥AF,可得∠BED=∠BFA,再根据三角形外角性质,即可得到∠BFA=20°+60°=80°,进而得出∠BED=80°.
【解答】解:如图所示,∵DE∥AF,
∴∠BED=∠BFA,
又∵∠CAF=20°,∠C=60°,
∴∠BFA=20°+60°=80°,
∴∠BED=80°,
故答案为:80.
25.(2018?通辽)如图,∠AOB的一边OA为平面镜,∠AOB=37°45′,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 75°30′(或75.5°) .
【分析】首先证明∠EDO=∠AOB=37°45′,根据∠DEB=∠AOB+∠EDO计算即可解决问题;
【解答】解:∵CD∥OB,
∴∠ADC=∠AOB,
∵∠EDO=∠CDA,
∴∠EDO=∠AOB=37°45′,
∴∠DEB=∠AOB+∠EDO=2×37°45′=75°30′(或75.5°),
故答案为75°30′(或75.5°).
26.(2018?衡阳)将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 75° .
【分析】先根据BC∥DE及三角板的度数求出∠EAB的度数,再根据三角形内角与外角的性质即可求出∠AFC的度数.
【解答】解:∵BC∥DE,△ABC为等腰直角三角形,
∴∠FBC=∠EAB=(180°﹣90°)=45°,
∵∠AFC是△AEF的外角,
∴∠AFC=∠FAE+∠E=45°+30°=75°.
故答案为:75°.
27.(2017?本溪)如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 130° .
【分析】依据平行线的性质,即可得到∠ABC以及∠2的度数.
【解答】解:∵AD∥BC,AB∥CD,
∴∠1=∠ABC=50°,
∴∠2=180°﹣∠ABC=180°﹣50°=130°,
故答案为:130°.
28.(2017?巴彦淖尔)如图,直线l1∥l2,则∠1+∠2= 30° .
【分析】先利用三角形外角性质得∠1+∠3=125°,∠2+∠4=85°,把两式相加得到∠1+∠3+∠2+∠4=210°,再根据平行线的性质,由l1∥l2得到∠3+∠4=180°,然后通过角度的计算得到∠1+∠2的度数.
【解答】解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为:30°.
29.(2017?阜新)如图,直线a∥b,AB⊥BC,如果∠1=35°,那么∠2的度数为 55° .
【分析】平行线的性质即可得出∠BDE的度数,由垂线的性质和对顶角的定义即可得到求出∠2的度数.
【解答】解:如图,∵a∥b,
∴∠BDE=∠1=35°,
∵AB⊥BC,
∴Rt△BDE中,∠BED=90°﹣35°=55°,
∴∠2=∠BED=55°,
故答案为:55°.
30.(2017?张家界)如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 55° .
【分析】先延长AP交直线b于C,再根据平行线的性质以及三角形的外角性质进行计算即可.
【解答】解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
31.(2017?岳阳)如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 60° .
【分析】根据PQ∥ON,即可得到∠QPD=∠PDO=90°,再根据平角的定义,即可得到∠MPQ.
【解答】解:∵PD⊥ON于点D,
∴∠PDO=90°,
又∵PQ∥ON,
∴∠QPD=∠PDO=90°,
∵∠OPD=30°,
∴∠MPQ=180°﹣∠QPD﹣∠OPD=180°﹣90°﹣30°=60°.
故答案为:60°.
32.(2017?金华)如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= 20° .
【分析】先根据平行线的性质,得到∠BDC=50°,再根据∠ADB=30°,即可得出∠2=20°.
【解答】解:∵∠1=130°,
∴∠3=50°,
又∵l1∥l2,
∴∠BDC=50°,
又∵∠ADB=30°,
∴∠2=20°,
故答案为:20°.
33.(2016?镇江)如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= 70 °.
【分析】根据平角等于180°列式计算得到∠3,根据两直线平行,同位角相等可得∠3=∠2.
【解答】解:∵∠1=20°,
∴∠3=90°﹣∠1=70°,
∵直线a∥b,
∴∠2=∠3=70°,
故答案是:70.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
