第三章 变量之间的关系复习题---填空题(含解析)
文档属性
| 名称 | 第三章 变量之间的关系复习题---填空题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 10:41:07 | ||
图片预览




文档简介
北师大版数学七下第三章变量之间的关系复习题---填空题
一.填空题
1.(2018春?青龙县期末)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
2.(2018春?灞桥区期中)某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
3.(2018春?云岩区校级期中)如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是 ,因变量是 ;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了 cm3.
4.(2018春?三亚期末)圆周长C与圆的半径r之间的关系为C=2πr,其中变量是 ,常量是 .
5.(2018春?太原期中)地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
Y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为 km.
6.(2018春?岱岳区期末)某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶 小时,油箱的余油量为0.
7.(2018春?沙坪坝区校级期中)声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖 米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
8.(2018秋?东城区期末)港珠澳大桥于2018年10月24日正式通车.大桥在设计理念、建造技术、施工组织、管理模式等方面进行一系列创新,标志着我国岛隧工程设计施工管理水平走在了世界前列.大桥全长近55km.汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为
9.(2018秋?新密市校级期中)米店买米,数量x(千克)与售价y(元)之间的关系如下表:
x/千克
0.5
1
1.5
2
…
y/元
1.3+0.1
2.6+0.1
3.9+0.1
5.2+0.1
…
则售价y与数量x之间的关系式是 .
10.(2017秋?单县期末)某工程队承建一条长为30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y= .
11.(2018春?沙坪坝区校级期末)某商场销售A,B两种足球服,成本均为60元,A球服标价100元,B球服标价120元,世界杯期间为了回馈广大球迷,A球服按八折销售,B球服每件优惠30元,已知A球服共卖出x件,B球服的销量是A球服的2倍还少3件,商场共获利y元,则化简后y与x之间的关系式为: .(不必写出x的取值范围)
12.(2018秋?锡山区校级期中)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示,秋千摆动第一个来回需 s?
13.(2018春?长清区期中)某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是 m2.
14.(2018春?沙坪坝区校级期末)某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家 米.
15.(2018春?镇平县期中)汽车开始行驶时,油箱内有油40L,油箱内的余油量Q(L)与行驶时间t(h)之间的函数关系的图象如图所示,则每小时耗油 L.
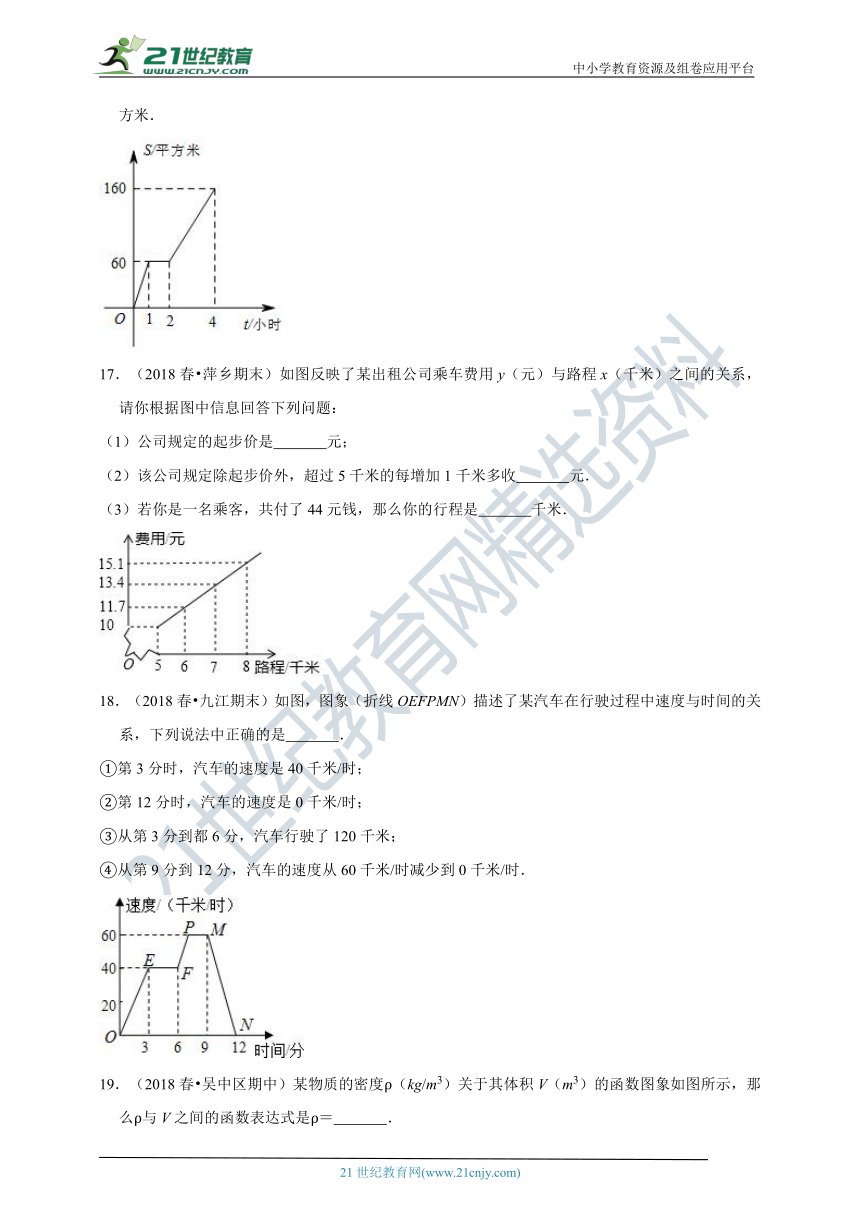
16.(2018春?成华区期末)园林队在某公司进行绿化,中间休息了一段时间,已知绿化面积S(平方米)与工作时间t(小时)的关系的图象如图所示,则休息后园林队每小时绿化面积为 平方米.
17.(2018春?萍乡期末)如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元.
(3)若你是一名乘客,共付了44元钱,那么你的行程是 千米.
18.(2018春?九江期末)如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是 .
①第3分时,汽车的速度是40千米/时;
②第12分时,汽车的速度是0千米/时;
③从第3分到都6分,汽车行驶了120千米;
④从第9分到12分,汽车的速度从60千米/时减少到0千米/时.
19.(2018春?吴中区期中)某物质的密度ρ(kg/m3)关于其体积V(m3)的函数图象如图所示,那么ρ与V之间的函数表达式是ρ= .
20.(2018春?鄄城县期中)经科学家研究,蝉在气温超过28℃时才会活跃起来,此时边吸树木的汁液边鸣叫,如图是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间是 小时.
21.(2018?上虞区模拟)如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为 cm.
22.(2018?盘锦)如图①,在矩形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图②所示,则矩形ABCD的面积为 .
23.(2018?枣庄)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
24.(2017?阜新)如图1.在四边形ABCD中,AB∥CD,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图2所示,那么AB边的长度为 .
25.(2018秋?泰兴市校级期中)如图1,在△ABC中,点P从点A出发向点C运动,在运动过程中,设x表示线段AP的长,y表示线段BP的长,y与x之间的关系如图2所示,则线段BC的长为 .
26.(2018春?嘉祥县期末)如图①,在?ABCD中,∠B=120°,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中H点的横坐标为 .
27.(2018?丹阳市模拟)在△ABC中,AH⊥BC于点H,点P从B点出发沿BC向C点运动,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q(1,)是函数图象上的最低点.当△ABP为锐角三角形时x的取值范围为 .
28.(2018?淮阳县校级一模)如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,且y与x之间的大致图象如图所示,则△APQ面积的最大值是 .
29.(2018?吉州区模拟)如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 .
北师大版数学七下第三章变量之间的关系复习题---填空题
参考答案与试题解析
一.填空题
1.(2018春?青龙县期末)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 电影票的售价 是常量, 电影票的张数,票房收入 是变量.
【分析】根据常量,变量的定义进行填空即可.
【解答】解:常量是电影票的售价,变量是电影票的张数,票房收入,
故答案为电影票的售价,电影票的张数,票房收入.
2.(2018春?灞桥区期中)某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 8 ,其中自变量是 年份 ,因变量是 分指数
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
【分析】通过所给数据应当发现:后边的每一个数据总是前面两个数据的和.
【解答】解:根据所给的具体数据发现:从第三个数据开始,每一个数据是前面两个数据的和,则第6年的时候是3+5=8个.
自变量是年份,因变量是分指数,
故答案为:8,年份,分指数.
3.(2018春?云岩区校级期中)如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是 半径 ,因变量是 体积 ;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了 297 cm3.
【分析】(1)根据常量和变量的定义来判断自变量、因变量和常量.
(2)利用圆柱的体积计算方法计算增加的体积即可.
【解答】解:(1)根据函数的定义可知,对于底面半径的每个值,体积按照一定的法则有一个确定的值与之对应,所以自变量是:半径,因变量是:体积.
(2)体积增加了(π×102﹣π×12)×3=297πcm3.
故答案为:(1)半径,体积;(2)297π.
4.(2018春?三亚期末)圆周长C与圆的半径r之间的关系为C=2πr,其中变量是 C、r ,常量是 2π .
【分析】根据函数的意义可知:变量是改变的量,常量是不变的量,据此即可确定变量与常量.
【解答】解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
故答案为:C,r;2π.
5.(2018春?太原期中)地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
Y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为 6 km.
【分析】直接利用根据题意得出函数解析式,进而得出x的值.
【解答】解:设Y=kx+b,
则把(1,55),(2,90)代入得:
,
解得:,
故Y=35k+20,
则当Y=230时,230=35x+20,
解得:x=6,
故答案为:6.
6.(2018春?岱岳区期末)某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶 12.5 小时,油箱的余油量为0.
【分析】由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少8L,据此可得y与t的关系式.
【解答】解:由题意可得:y=100﹣8t,
当y=0时,0=100﹣8t
解得:t=12.5.
故答案为:12.5.
7.(2018春?沙坪坝区校级期中)声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖 692 米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
【分析】直接利用表格得出声音在空气中传播的速度,进而得出答案.
【解答】解:由题意可得:气温为25℃,声音在空气中传播的速度为346米/秒,
∵驾驶员按响喇叭,4s后听到回声,
∴汽车距山崖346×4÷2=692(米),
故答案为:692.
8.(2018秋?东城区期末)港珠澳大桥于2018年10月24日正式通车.大桥在设计理念、建造技术、施工组织、管理模式等方面进行一系列创新,标志着我国岛隧工程设计施工管理水平走在了世界前列.大桥全长近55km.汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为
【分析】依据行程问题中的关系:时间=路程÷速度,即可得到汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式.
【解答】解:∵大桥全长近55km,
∴汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为,
故答案为:.
9.(2018秋?新密市校级期中)米店买米,数量x(千克)与售价y(元)之间的关系如下表:
x/千克
0.5
1
1.5
2
…
y/元
1.3+0.1
2.6+0.1
3.9+0.1
5.2+0.1
…
则售价y与数量x之间的关系式是 y=2.6x+0.1 .
【分析】根据观察,可发现规律:每增加0.5千克,售价增加1.3元,可得答案.
【解答】解:售价y与数量x之间的关系式是y=2.6x+0.1,
故答案为:y=2.6x+0.1.
10.(2017秋?单县期末)某工程队承建一条长为30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y= 30﹣x .
【分析】根据总工程量减去已修的工程量,可得答案.
【解答】解:由题意,得
每天修30÷120=km,
y=30﹣x,
故答案为:30﹣x.
11.(2018春?沙坪坝区校级期末)某商场销售A,B两种足球服,成本均为60元,A球服标价100元,B球服标价120元,世界杯期间为了回馈广大球迷,A球服按八折销售,B球服每件优惠30元,已知A球服共卖出x件,B球服的销量是A球服的2倍还少3件,商场共获利y元,则化简后y与x之间的关系式为: y=80x﹣90 .(不必写出x的取值范围)
【分析】根据总利润=(打折后每件A球服的售价﹣成本价)×A球服的销售数量+(优惠后每件B球服的售价﹣成本价)×B球服的销售数量,即可得出y与x之间的关系式,化简后即可得出结论.
【解答】解:根据题意得:y=(0.8×100﹣60)x+(120﹣30﹣60)(2x﹣3),
化简得:y=80x﹣90.
故答案为:y=80x﹣90.
12.(2018秋?锡山区校级期中)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示,秋千摆动第一个来回需 2.8 s?
【分析】结合荡秋千的经验,秋千先从一端的最高点下落到最低点,再荡到另一端的最高点,再返回到最低点,最后回到开始的一端,符合这一过程的即是0~2.8s,由此即可得出结论.
【解答】解:观察函数图象,可知:秋千摆动第一个来回需2.8s.
故答案为:2.8.
13.(2018春?长清区期中)某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是 150 m2.
【分析】根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
【解答】解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
故答案为:150
14.(2018春?沙坪坝区校级期末)某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家 1350 米.
【分析】先根据题意求得两人在第20分钟相遇时小明的路程为3600米,再根据小颖先到并停留了8分钟且往返速度相等得出小颖的速度及公园距离小颖家的距离,进一步求解可得.
【解答】解:由题意知,小颖去往公园耗时10分钟,且停留8分钟,
∴小颖原路返回时间为第18分钟,
∵小颖往返速度相等,
∴小颖返回到达时刻为第28分钟,
由小明的速度为180米/分钟知,两人在第20分钟相遇时,小明的路程为20×180=3600(米),
∴小颖的速度为3600÷(28﹣20)=450(米/分钟),
则公园距离小颖家的距离为450×10=4500(米),
∴小明到达公园的时刻为第4500÷180=25(分钟),
则当小明到达公园的时候小颖离家450×(28﹣25)=1350(米),
故答案为:1350.
15.(2018春?镇平县期中)汽车开始行驶时,油箱内有油40L,油箱内的余油量Q(L)与行驶时间t(h)之间的函数关系的图象如图所示,则每小时耗油 5 L.
【分析】根据函数图象得到40L油,8h后余油量为0,计算即可.
【解答】解:由函数图象可知,40L油,8h后余油量为0,
则每小时耗油:40÷8=5(L),
故答案为:5.
16.(2018春?成华区期末)园林队在某公司进行绿化,中间休息了一段时间,已知绿化面积S(平方米)与工作时间t(小时)的关系的图象如图所示,则休息后园林队每小时绿化面积为 50 平方米.
【分析】根据休息后2小时的绿化面积100平方米,即可判断;
【解答】解:休息后2小时内绿化面积为160﹣60=100平方米.
∴休息后园林队每小时绿化面积为.
故答案为:50
17.(2018春?萍乡期末)如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 10 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 1.7 元.
(3)若你是一名乘客,共付了44元钱,那么你的行程是 25 千米.
【分析】(1)根据图象的信息解答即可;
(2)根据图象信息解答即可;
(3)得出解析式后代入数值解答即可.
【解答】解:(1)由图象可得:公司规定的起步价是10元;
(2)由图象可得:该公司规定除起步价外,超过5千米的每增加1千米多收11.7﹣10=1.7元;
(3)由图象可得函数解析式为:y=10+(x﹣5)×1.7,
把y=44代入解析式可得:44=10+(x﹣5)×1.7,
解得:x=25,
故答案为:10;1.7;25.
18.(2018春?九江期末)如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是 ①②④ .
①第3分时,汽车的速度是40千米/时;
②第12分时,汽车的速度是0千米/时;
③从第3分到都6分,汽车行驶了120千米;
④从第9分到12分,汽车的速度从60千米/时减少到0千米/时.
【分析】根据图象反映的速度与时间的关系,可以计算路程,针对每一个选项,逐一判断.
【解答】解:横轴表示时间,纵轴表示速度.
当第3分的时候,对应的速度是40千米/时,故①对;
第12分的时候,对应的速度是0千米/时,故②对;
从第3分到第6分,汽车的速度保持不变,是40千米/时,行驶的路程为40×=2千米,故③错;
从第9分到第12分,汽车对应的速度分别是60千米/时,0千米/时,所以汽车的速度从60千米/时减少到0千米/时,故④对.
综上可得:正确的是①②④.
故答案为:①②④.
19.(2018春?吴中区期中)某物质的密度ρ(kg/m3)关于其体积V(m3)的函数图象如图所示,那么ρ与V之间的函数表达式是ρ= .
【分析】根据图象可得物质的密度p(kg/m3)关于其体积V(m3)的函数关系式为反比例函数形式,设p=,再把(6,2)代入函数关系式可得k的值,进而得到反比函数关系式.
【解答】解:设物质的密度p(kg/m3)关于其体积V(m3)的函数关系式为p=,
∵函数图象经过(6,2),
∴k=6×2=12,
∴p=,
故答案为:.
20.(2018春?鄄城县期中)经科学家研究,蝉在气温超过28℃时才会活跃起来,此时边吸树木的汁液边鸣叫,如图是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间是 12 小时.
【分析】根据函数图象的横坐标,可得答案.
【解答】解:图象不超过28°的时间是10﹣0=10,24﹣22=2,
10+2=12小时,
故答案为:12.
21.(2018?上虞区模拟)如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为 2 cm.
【分析】由注满相同高度的水乙容器所需的时间为甲容器的4倍,结合甲容器的底面半径即可求出乙容器的底面半径,此题得解.
【解答】解:观察函数图象可知:乙容器底面积为甲容器底面积的4倍,
∴乙容器底面半径为2cm.
故答案为:2
22.(2018?盘锦)如图①,在矩形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图②所示,则矩形ABCD的面积为 24 .
【分析】根据图象②得出AB、BC的长度,再求出面积即可.
【解答】解:从图象②和已知可知:AB=4,BC=10﹣4=6,
所以矩形ABCD的面积是4×6=24,
故答案为:24.
23.(2018?枣庄)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 12 .
【分析】根据图象可知点P在BC上运动时,此时BP不断增大,而从C向A运动时,BP先变小后变大,从而可求出BC与AC的长度.
【解答】解:根据图象可知点P在BC上运动时,此时BP不断增大,
由图象可知:点P从B向C运动时,BP的最大值为5,
即BC=5,
由于M是曲线部分的最低点,
∴此时BP最小,
即BP⊥AC,BP=4,
∴由勾股定理可知:PC=3,
由于图象的曲线部分是轴对称图形,
∴PA=3,
∴AC=6,
∴△ABC的面积为:×4×6=12
故答案为:12
24.(2017?阜新)如图1.在四边形ABCD中,AB∥CD,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图2所示,那么AB边的长度为 6 .
【分析】根据题意,分析P的运动路线,分3个阶段分别讨论,可得BC,CD,DA的值,过D作DE⊥AB于E,根据勾股定理求得AE,进而可得答案.
【解答】解:根据题意,
当P在BC上时,三角形面积增大,结合图2可得,BC=4;
当P在CD上时,三角形面积不变,结合图2可得,CD=3;
当P在DA上时,三角形面积变小,结合图2可得,DA=5;
过D作DE⊥AB于E,
∵AB∥CD,AB⊥BC,
∴四边形DEBC是矩形,
∴EB=CD=3,DE=BC=4,AE===3,
∴AB=AE+EB=3+3=6,
故答案为:6.
25.(2018秋?泰兴市校级期中)如图1,在△ABC中,点P从点A出发向点C运动,在运动过程中,设x表示线段AP的长,y表示线段BP的长,y与x之间的关系如图2所示,则线段BC的长为 .
【分析】分析当点P在点A处、点P到达AC边高(BP)的位置、AP到达点C处,P点的位置对应2个图中的位置关系,即可求解.
【解答】解:如下图所示,
①当点P在点A处时,即AP=0,对应图2的点D,即:AB=2,
②当点P到达AC边高(BP)的位置时,AP=1,对应图2的点E处,此时BP最小,即BP==,
③当AP=5时,点P对应图2点F处,即AC=5,则PC=AC﹣AP=5﹣1=4,
则:BC===,
故答案是.
26.(2018春?嘉祥县期末)如图①,在?ABCD中,∠B=120°,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中H点的横坐标为 14 .
【分析】根据图象点P到达C时,△PAB的面积为6,由BC=4,∠B=120°可求得AB=6,H横坐标表示点P从B开始运动到A的总路程,则问题可解.
【解答】解:由图象可知,当x=4时,点P到达C点,此时△PAB的面积为6
∵∠B=120°,BC=4
∴
解得AB=6
H点表示点P到达A时运动的路程为4+6+4=14
故答案为:14
27.(2018?丹阳市模拟)在△ABC中,AH⊥BC于点H,点P从B点出发沿BC向C点运动,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q(1,)是函数图象上的最低点.当△ABP为锐角三角形时x的取值范围为 1<x<4 .
【分析】根据题意得到BH、AH长度,分类讨论△ABP为直角三角形时的情况即可.
【解答】解:根据题意,AB=2,点A到BC的距离为,此时P到H,BP=1.
当点C与点H重合时,△ABP为直角三角形.则C在H右侧时,△ABP为锐角三角形.
当∠BAC=90°时,△AHB∽△CHA,则有AH2=BH?HC
∴()2=1?HC
HC=3
∴BC=4
当△ABP为锐角三角形时,1<x<4
故答案为:1<x<4
28.(2018?淮阳县校级一模)如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,且y与x之间的大致图象如图所示,则△APQ面积的最大值是 32 .
【分析】根据题意结合图象,得到AB和点Q与C重合时AP得到此时PQ长,通过锐角三角函数得到∠B=60°,表示当12≤x≤16时,△APQ面积讨论最值即可.
【解答】解:由图象可知,当点Q与点C重合时,AP=12
当点P与点B重合时,AB=16
则由射影定理可知点C到AB距离为4
由锐角三角形函数可知∴∠A=30°
则∠B=60°
当12≤x≤16时,
PB=16﹣x,QB=
△APQ的面积y=
当x=8时,y最大=32
故答案为:32
29.(2018?吉州区模拟)如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 20 .
【分析】根据图象横坐标的变化,问题可解.
【解答】解:由图象可知,x=4时,点R到达P,x=9时,点R到Q点,则PN=4,QP=5
∴矩形MNPQ的面积是20.
一.填空题
1.(2018春?青龙县期末)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
2.(2018春?灞桥区期中)某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
3.(2018春?云岩区校级期中)如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是 ,因变量是 ;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了 cm3.
4.(2018春?三亚期末)圆周长C与圆的半径r之间的关系为C=2πr,其中变量是 ,常量是 .
5.(2018春?太原期中)地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
Y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为 km.
6.(2018春?岱岳区期末)某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶 小时,油箱的余油量为0.
7.(2018春?沙坪坝区校级期中)声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖 米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
8.(2018秋?东城区期末)港珠澳大桥于2018年10月24日正式通车.大桥在设计理念、建造技术、施工组织、管理模式等方面进行一系列创新,标志着我国岛隧工程设计施工管理水平走在了世界前列.大桥全长近55km.汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为
9.(2018秋?新密市校级期中)米店买米,数量x(千克)与售价y(元)之间的关系如下表:
x/千克
0.5
1
1.5
2
…
y/元
1.3+0.1
2.6+0.1
3.9+0.1
5.2+0.1
…
则售价y与数量x之间的关系式是 .
10.(2017秋?单县期末)某工程队承建一条长为30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y= .
11.(2018春?沙坪坝区校级期末)某商场销售A,B两种足球服,成本均为60元,A球服标价100元,B球服标价120元,世界杯期间为了回馈广大球迷,A球服按八折销售,B球服每件优惠30元,已知A球服共卖出x件,B球服的销量是A球服的2倍还少3件,商场共获利y元,则化简后y与x之间的关系式为: .(不必写出x的取值范围)
12.(2018秋?锡山区校级期中)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示,秋千摆动第一个来回需 s?
13.(2018春?长清区期中)某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是 m2.
14.(2018春?沙坪坝区校级期末)某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家 米.
15.(2018春?镇平县期中)汽车开始行驶时,油箱内有油40L,油箱内的余油量Q(L)与行驶时间t(h)之间的函数关系的图象如图所示,则每小时耗油 L.
16.(2018春?成华区期末)园林队在某公司进行绿化,中间休息了一段时间,已知绿化面积S(平方米)与工作时间t(小时)的关系的图象如图所示,则休息后园林队每小时绿化面积为 平方米.
17.(2018春?萍乡期末)如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元.
(3)若你是一名乘客,共付了44元钱,那么你的行程是 千米.
18.(2018春?九江期末)如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是 .
①第3分时,汽车的速度是40千米/时;
②第12分时,汽车的速度是0千米/时;
③从第3分到都6分,汽车行驶了120千米;
④从第9分到12分,汽车的速度从60千米/时减少到0千米/时.
19.(2018春?吴中区期中)某物质的密度ρ(kg/m3)关于其体积V(m3)的函数图象如图所示,那么ρ与V之间的函数表达式是ρ= .
20.(2018春?鄄城县期中)经科学家研究,蝉在气温超过28℃时才会活跃起来,此时边吸树木的汁液边鸣叫,如图是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间是 小时.
21.(2018?上虞区模拟)如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为 cm.
22.(2018?盘锦)如图①,在矩形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图②所示,则矩形ABCD的面积为 .
23.(2018?枣庄)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
24.(2017?阜新)如图1.在四边形ABCD中,AB∥CD,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图2所示,那么AB边的长度为 .
25.(2018秋?泰兴市校级期中)如图1,在△ABC中,点P从点A出发向点C运动,在运动过程中,设x表示线段AP的长,y表示线段BP的长,y与x之间的关系如图2所示,则线段BC的长为 .
26.(2018春?嘉祥县期末)如图①,在?ABCD中,∠B=120°,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中H点的横坐标为 .
27.(2018?丹阳市模拟)在△ABC中,AH⊥BC于点H,点P从B点出发沿BC向C点运动,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q(1,)是函数图象上的最低点.当△ABP为锐角三角形时x的取值范围为 .
28.(2018?淮阳县校级一模)如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,且y与x之间的大致图象如图所示,则△APQ面积的最大值是 .
29.(2018?吉州区模拟)如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 .
北师大版数学七下第三章变量之间的关系复习题---填空题
参考答案与试题解析
一.填空题
1.(2018春?青龙县期末)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 电影票的售价 是常量, 电影票的张数,票房收入 是变量.
【分析】根据常量,变量的定义进行填空即可.
【解答】解:常量是电影票的售价,变量是电影票的张数,票房收入,
故答案为电影票的售价,电影票的张数,票房收入.
2.(2018春?灞桥区期中)某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 8 ,其中自变量是 年份 ,因变量是 分指数
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
【分析】通过所给数据应当发现:后边的每一个数据总是前面两个数据的和.
【解答】解:根据所给的具体数据发现:从第三个数据开始,每一个数据是前面两个数据的和,则第6年的时候是3+5=8个.
自变量是年份,因变量是分指数,
故答案为:8,年份,分指数.
3.(2018春?云岩区校级期中)如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是 半径 ,因变量是 体积 ;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了 297 cm3.
【分析】(1)根据常量和变量的定义来判断自变量、因变量和常量.
(2)利用圆柱的体积计算方法计算增加的体积即可.
【解答】解:(1)根据函数的定义可知,对于底面半径的每个值,体积按照一定的法则有一个确定的值与之对应,所以自变量是:半径,因变量是:体积.
(2)体积增加了(π×102﹣π×12)×3=297πcm3.
故答案为:(1)半径,体积;(2)297π.
4.(2018春?三亚期末)圆周长C与圆的半径r之间的关系为C=2πr,其中变量是 C、r ,常量是 2π .
【分析】根据函数的意义可知:变量是改变的量,常量是不变的量,据此即可确定变量与常量.
【解答】解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
故答案为:C,r;2π.
5.(2018春?太原期中)地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
Y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为 6 km.
【分析】直接利用根据题意得出函数解析式,进而得出x的值.
【解答】解:设Y=kx+b,
则把(1,55),(2,90)代入得:
,
解得:,
故Y=35k+20,
则当Y=230时,230=35x+20,
解得:x=6,
故答案为:6.
6.(2018春?岱岳区期末)某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶 12.5 小时,油箱的余油量为0.
【分析】由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少8L,据此可得y与t的关系式.
【解答】解:由题意可得:y=100﹣8t,
当y=0时,0=100﹣8t
解得:t=12.5.
故答案为:12.5.
7.(2018春?沙坪坝区校级期中)声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖 692 米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
【分析】直接利用表格得出声音在空气中传播的速度,进而得出答案.
【解答】解:由题意可得:气温为25℃,声音在空气中传播的速度为346米/秒,
∵驾驶员按响喇叭,4s后听到回声,
∴汽车距山崖346×4÷2=692(米),
故答案为:692.
8.(2018秋?东城区期末)港珠澳大桥于2018年10月24日正式通车.大桥在设计理念、建造技术、施工组织、管理模式等方面进行一系列创新,标志着我国岛隧工程设计施工管理水平走在了世界前列.大桥全长近55km.汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为
【分析】依据行程问题中的关系:时间=路程÷速度,即可得到汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式.
【解答】解:∵大桥全长近55km,
∴汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为,
故答案为:.
9.(2018秋?新密市校级期中)米店买米,数量x(千克)与售价y(元)之间的关系如下表:
x/千克
0.5
1
1.5
2
…
y/元
1.3+0.1
2.6+0.1
3.9+0.1
5.2+0.1
…
则售价y与数量x之间的关系式是 y=2.6x+0.1 .
【分析】根据观察,可发现规律:每增加0.5千克,售价增加1.3元,可得答案.
【解答】解:售价y与数量x之间的关系式是y=2.6x+0.1,
故答案为:y=2.6x+0.1.
10.(2017秋?单县期末)某工程队承建一条长为30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y= 30﹣x .
【分析】根据总工程量减去已修的工程量,可得答案.
【解答】解:由题意,得
每天修30÷120=km,
y=30﹣x,
故答案为:30﹣x.
11.(2018春?沙坪坝区校级期末)某商场销售A,B两种足球服,成本均为60元,A球服标价100元,B球服标价120元,世界杯期间为了回馈广大球迷,A球服按八折销售,B球服每件优惠30元,已知A球服共卖出x件,B球服的销量是A球服的2倍还少3件,商场共获利y元,则化简后y与x之间的关系式为: y=80x﹣90 .(不必写出x的取值范围)
【分析】根据总利润=(打折后每件A球服的售价﹣成本价)×A球服的销售数量+(优惠后每件B球服的售价﹣成本价)×B球服的销售数量,即可得出y与x之间的关系式,化简后即可得出结论.
【解答】解:根据题意得:y=(0.8×100﹣60)x+(120﹣30﹣60)(2x﹣3),
化简得:y=80x﹣90.
故答案为:y=80x﹣90.
12.(2018秋?锡山区校级期中)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示,秋千摆动第一个来回需 2.8 s?
【分析】结合荡秋千的经验,秋千先从一端的最高点下落到最低点,再荡到另一端的最高点,再返回到最低点,最后回到开始的一端,符合这一过程的即是0~2.8s,由此即可得出结论.
【解答】解:观察函数图象,可知:秋千摆动第一个来回需2.8s.
故答案为:2.8.
13.(2018春?长清区期中)某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是 150 m2.
【分析】根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
【解答】解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
故答案为:150
14.(2018春?沙坪坝区校级期末)某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家 1350 米.
【分析】先根据题意求得两人在第20分钟相遇时小明的路程为3600米,再根据小颖先到并停留了8分钟且往返速度相等得出小颖的速度及公园距离小颖家的距离,进一步求解可得.
【解答】解:由题意知,小颖去往公园耗时10分钟,且停留8分钟,
∴小颖原路返回时间为第18分钟,
∵小颖往返速度相等,
∴小颖返回到达时刻为第28分钟,
由小明的速度为180米/分钟知,两人在第20分钟相遇时,小明的路程为20×180=3600(米),
∴小颖的速度为3600÷(28﹣20)=450(米/分钟),
则公园距离小颖家的距离为450×10=4500(米),
∴小明到达公园的时刻为第4500÷180=25(分钟),
则当小明到达公园的时候小颖离家450×(28﹣25)=1350(米),
故答案为:1350.
15.(2018春?镇平县期中)汽车开始行驶时,油箱内有油40L,油箱内的余油量Q(L)与行驶时间t(h)之间的函数关系的图象如图所示,则每小时耗油 5 L.
【分析】根据函数图象得到40L油,8h后余油量为0,计算即可.
【解答】解:由函数图象可知,40L油,8h后余油量为0,
则每小时耗油:40÷8=5(L),
故答案为:5.
16.(2018春?成华区期末)园林队在某公司进行绿化,中间休息了一段时间,已知绿化面积S(平方米)与工作时间t(小时)的关系的图象如图所示,则休息后园林队每小时绿化面积为 50 平方米.
【分析】根据休息后2小时的绿化面积100平方米,即可判断;
【解答】解:休息后2小时内绿化面积为160﹣60=100平方米.
∴休息后园林队每小时绿化面积为.
故答案为:50
17.(2018春?萍乡期末)如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 10 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 1.7 元.
(3)若你是一名乘客,共付了44元钱,那么你的行程是 25 千米.
【分析】(1)根据图象的信息解答即可;
(2)根据图象信息解答即可;
(3)得出解析式后代入数值解答即可.
【解答】解:(1)由图象可得:公司规定的起步价是10元;
(2)由图象可得:该公司规定除起步价外,超过5千米的每增加1千米多收11.7﹣10=1.7元;
(3)由图象可得函数解析式为:y=10+(x﹣5)×1.7,
把y=44代入解析式可得:44=10+(x﹣5)×1.7,
解得:x=25,
故答案为:10;1.7;25.
18.(2018春?九江期末)如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是 ①②④ .
①第3分时,汽车的速度是40千米/时;
②第12分时,汽车的速度是0千米/时;
③从第3分到都6分,汽车行驶了120千米;
④从第9分到12分,汽车的速度从60千米/时减少到0千米/时.
【分析】根据图象反映的速度与时间的关系,可以计算路程,针对每一个选项,逐一判断.
【解答】解:横轴表示时间,纵轴表示速度.
当第3分的时候,对应的速度是40千米/时,故①对;
第12分的时候,对应的速度是0千米/时,故②对;
从第3分到第6分,汽车的速度保持不变,是40千米/时,行驶的路程为40×=2千米,故③错;
从第9分到第12分,汽车对应的速度分别是60千米/时,0千米/时,所以汽车的速度从60千米/时减少到0千米/时,故④对.
综上可得:正确的是①②④.
故答案为:①②④.
19.(2018春?吴中区期中)某物质的密度ρ(kg/m3)关于其体积V(m3)的函数图象如图所示,那么ρ与V之间的函数表达式是ρ= .
【分析】根据图象可得物质的密度p(kg/m3)关于其体积V(m3)的函数关系式为反比例函数形式,设p=,再把(6,2)代入函数关系式可得k的值,进而得到反比函数关系式.
【解答】解:设物质的密度p(kg/m3)关于其体积V(m3)的函数关系式为p=,
∵函数图象经过(6,2),
∴k=6×2=12,
∴p=,
故答案为:.
20.(2018春?鄄城县期中)经科学家研究,蝉在气温超过28℃时才会活跃起来,此时边吸树木的汁液边鸣叫,如图是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间是 12 小时.
【分析】根据函数图象的横坐标,可得答案.
【解答】解:图象不超过28°的时间是10﹣0=10,24﹣22=2,
10+2=12小时,
故答案为:12.
21.(2018?上虞区模拟)如图(1)是两圆柱形联通容器(联通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为 2 cm.
【分析】由注满相同高度的水乙容器所需的时间为甲容器的4倍,结合甲容器的底面半径即可求出乙容器的底面半径,此题得解.
【解答】解:观察函数图象可知:乙容器底面积为甲容器底面积的4倍,
∴乙容器底面半径为2cm.
故答案为:2
22.(2018?盘锦)如图①,在矩形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图②所示,则矩形ABCD的面积为 24 .
【分析】根据图象②得出AB、BC的长度,再求出面积即可.
【解答】解:从图象②和已知可知:AB=4,BC=10﹣4=6,
所以矩形ABCD的面积是4×6=24,
故答案为:24.
23.(2018?枣庄)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 12 .
【分析】根据图象可知点P在BC上运动时,此时BP不断增大,而从C向A运动时,BP先变小后变大,从而可求出BC与AC的长度.
【解答】解:根据图象可知点P在BC上运动时,此时BP不断增大,
由图象可知:点P从B向C运动时,BP的最大值为5,
即BC=5,
由于M是曲线部分的最低点,
∴此时BP最小,
即BP⊥AC,BP=4,
∴由勾股定理可知:PC=3,
由于图象的曲线部分是轴对称图形,
∴PA=3,
∴AC=6,
∴△ABC的面积为:×4×6=12
故答案为:12
24.(2017?阜新)如图1.在四边形ABCD中,AB∥CD,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图2所示,那么AB边的长度为 6 .
【分析】根据题意,分析P的运动路线,分3个阶段分别讨论,可得BC,CD,DA的值,过D作DE⊥AB于E,根据勾股定理求得AE,进而可得答案.
【解答】解:根据题意,
当P在BC上时,三角形面积增大,结合图2可得,BC=4;
当P在CD上时,三角形面积不变,结合图2可得,CD=3;
当P在DA上时,三角形面积变小,结合图2可得,DA=5;
过D作DE⊥AB于E,
∵AB∥CD,AB⊥BC,
∴四边形DEBC是矩形,
∴EB=CD=3,DE=BC=4,AE===3,
∴AB=AE+EB=3+3=6,
故答案为:6.
25.(2018秋?泰兴市校级期中)如图1,在△ABC中,点P从点A出发向点C运动,在运动过程中,设x表示线段AP的长,y表示线段BP的长,y与x之间的关系如图2所示,则线段BC的长为 .
【分析】分析当点P在点A处、点P到达AC边高(BP)的位置、AP到达点C处,P点的位置对应2个图中的位置关系,即可求解.
【解答】解:如下图所示,
①当点P在点A处时,即AP=0,对应图2的点D,即:AB=2,
②当点P到达AC边高(BP)的位置时,AP=1,对应图2的点E处,此时BP最小,即BP==,
③当AP=5时,点P对应图2点F处,即AC=5,则PC=AC﹣AP=5﹣1=4,
则:BC===,
故答案是.
26.(2018春?嘉祥县期末)如图①,在?ABCD中,∠B=120°,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中H点的横坐标为 14 .
【分析】根据图象点P到达C时,△PAB的面积为6,由BC=4,∠B=120°可求得AB=6,H横坐标表示点P从B开始运动到A的总路程,则问题可解.
【解答】解:由图象可知,当x=4时,点P到达C点,此时△PAB的面积为6
∵∠B=120°,BC=4
∴
解得AB=6
H点表示点P到达A时运动的路程为4+6+4=14
故答案为:14
27.(2018?丹阳市模拟)在△ABC中,AH⊥BC于点H,点P从B点出发沿BC向C点运动,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q(1,)是函数图象上的最低点.当△ABP为锐角三角形时x的取值范围为 1<x<4 .
【分析】根据题意得到BH、AH长度,分类讨论△ABP为直角三角形时的情况即可.
【解答】解:根据题意,AB=2,点A到BC的距离为,此时P到H,BP=1.
当点C与点H重合时,△ABP为直角三角形.则C在H右侧时,△ABP为锐角三角形.
当∠BAC=90°时,△AHB∽△CHA,则有AH2=BH?HC
∴()2=1?HC
HC=3
∴BC=4
当△ABP为锐角三角形时,1<x<4
故答案为:1<x<4
28.(2018?淮阳县校级一模)如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一点,过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,且y与x之间的大致图象如图所示,则△APQ面积的最大值是 32 .
【分析】根据题意结合图象,得到AB和点Q与C重合时AP得到此时PQ长,通过锐角三角函数得到∠B=60°,表示当12≤x≤16时,△APQ面积讨论最值即可.
【解答】解:由图象可知,当点Q与点C重合时,AP=12
当点P与点B重合时,AB=16
则由射影定理可知点C到AB距离为4
由锐角三角形函数可知∴∠A=30°
则∠B=60°
当12≤x≤16时,
PB=16﹣x,QB=
△APQ的面积y=
当x=8时,y最大=32
故答案为:32
29.(2018?吉州区模拟)如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 20 .
【分析】根据图象横坐标的变化,问题可解.
【解答】解:由图象可知,x=4时,点R到达P,x=9时,点R到Q点,则PN=4,QP=5
∴矩形MNPQ的面积是20.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
