第五章 生活中的轴对称复习题---选择题(含解析)
文档属性
| 名称 | 第五章 生活中的轴对称复习题---选择题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 10:59:00 | ||
图片预览




文档简介
北师大版数学七下第五章生活中的轴对称复习题---选择题
一.选择题
1.(2018?资阳)下列图形具有两条对称轴的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正方形
2.(2018?湘西州)下列四个图形中,是轴对称图形的是( )
A. B. C. D.
3.(2018?苏州)下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
4.(2018?宜昌)如下字体的四个汉字中,是轴对称图形的是( )
A. B. C. D.
5.(2018秋?新罗区校级期中)如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中,错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB,A′B′的交点不一定在直线MN上
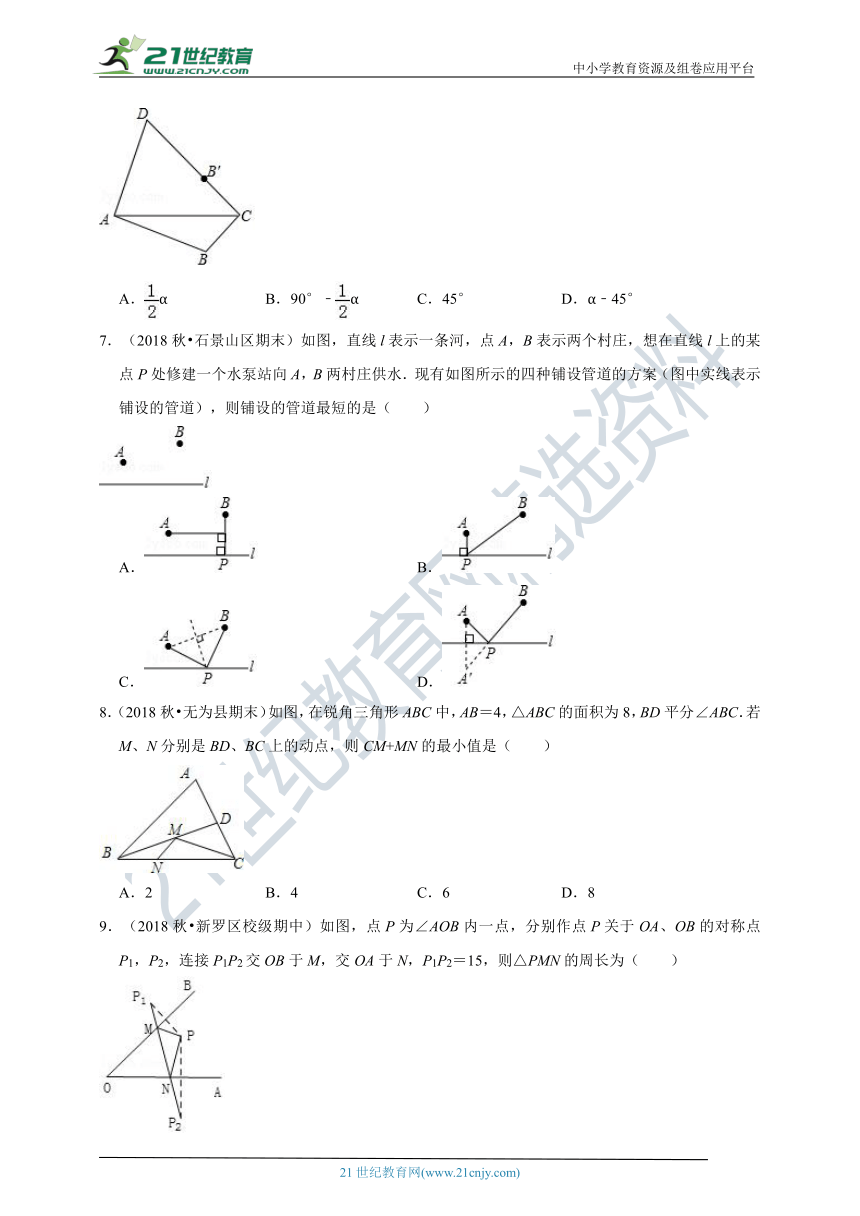
6.(2018秋?宜兴市期中)如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=α,则∠ACB的度数为( )
A.α B.90°﹣α C.45° D.α﹣45°
7.(2018秋?石景山区期末)如图,直线l表示一条河,点A,B表示两个村庄,想在直线l上的某点P处修建一个水泵站向A,B两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是( )
A. B.
C. D.
8.(2018秋?无为县期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
9.(2018秋?新罗区校级期中)如图,点P为∠AOB内一点,分别作点P关于OA、OB的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为( )
A.16 B.15 C.14 D.13
10.(2018秋?房山区期末)如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.64° C.65° D.70°
11.(2018秋?汝阳县期末)如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′=AA',则折痕DE的长为( )
A.4 B.3 C.2 D.
12.(2018?辽阳)如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5 B. C.4 D.
13.(2018?梧州)如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3 C.4 D.6
14.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
15.(2018秋?开封期中)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②AC=4BF;③DB=DC;④AD⊥BC,其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
16.(2018秋?巴南区期中)如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有( )
A.4个 B.3个 C.2个 D.1个
17.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
18.(2018秋?江门期末)如图,DE是△ABC中AC边的垂直平分线,若BC=6cm,AB=8cm,则△EBC的周长为( )
A.14cm B.18cm C.20cm D.22cm
19.(2018秋?南关区期末)如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
20.(2018秋?长春期末)如图,在△ABC中,边AC的垂直平分线交边AB于点D,连结CD.若∠A=50°,则∠BDC的大小为( )
A.90° B.100° C.120° D.130°
21.(2018秋?雨花区校级期中)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC长为12cm,BE长为8cm,则EC的长为( )
A.8cm B.6cm C.4cm D.2cm
22.(2018?兰州)如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
23.(2018?湖州)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
24.(2018秋?江门期末)等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
25.(2018秋?顺义区期末)等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
26.(2018秋?朝阳区期末)如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
A.∠ACD=2∠A B.∠A=2∠P C.BP⊥AC D.BC=CP
北师大版数学七下第五章生活中的轴对称复习题---选择题
参考答案与试题解析
一.选择题
1.(2018?资阳)下列图形具有两条对称轴的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正方形
【分析】根据轴对称及对称轴的定义,结合所给图形即可作出判断.
【解答】解:A、等边三角形由3条对称轴,故本选项错误;
B、平行四边形无对称轴,故本选项错误;
C、矩形有2条对称轴,故本选项正确;
D、正方形有4条对称轴,故本选项错误;
故选:C.
2.(2018?湘西州)下列四个图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念求解.
【解答】解:D选项的图形是轴对称图形,A,B,C选项的图形不是轴对称图形.
故选:D.
3.(2018?苏州)下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
【分析】根据轴对称的概念对各选项分析判断利用排除法求解.
【解答】解:A、是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项正确;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:B.
4.(2018?宜昌)如下字体的四个汉字中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的定义逐个判断即可.
【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意;
故选:D.
5.(2018秋?新罗区校级期中)如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中,错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB,A′B′的交点不一定在直线MN上
【分析】据对称轴的定义,△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,可以判断出图中各点或线段之间的关系.
【解答】解:∵△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,
∴△AA′P是等腰三角形,MN垂直平分AA′,CC′,这两个三角形的面积相等,故A、B、C选项正确,
直线AB,A′B′关于直线MN对称,因此交点一定在MN上,故D错误,
故选:D.
6.(2018秋?宜兴市期中)如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=α,则∠ACB的度数为( )
A.α B.90°﹣α C.45° D.α﹣45°
【分析】连接AB',BB',过A作AE⊥CD于E,依据∠BAC=∠B'AC,∠DAE=∠B'AE,即可得出∠CAE=∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=∠ACB'=90°﹣∠BAD.
【解答】解:如图,连接AB',BB',过A作AE⊥CD于E,
∵点B关于AC的对称点B'恰好落在CD上,
∴AC垂直平分BB',
∴AB=AB',
∴∠BAC=∠B'AC,
∵AB=AD,
∴AD=AB',
又∵AE⊥CD,
∴∠DAE=∠B'AE,
∴∠CAE=∠BAD=,
又∵∠AEB'=∠AOB'=90°,
∴四边形AOB'E中,∠EB'O=180°﹣,
∴∠ACB'=∠EB'O﹣∠COB'=180°﹣﹣90°=90°﹣,
∴∠ACB=∠ACB'=90°﹣,
故选:B.
7.(2018秋?石景山区期末)如图,直线l表示一条河,点A,B表示两个村庄,想在直线l上的某点P处修建一个水泵站向A,B两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是( )
A. B.
C. D.
【分析】依据轴对称的性质,通过等线段代换,将所求路线长转化为两点之间的距离即可.
【解答】解:作点A关于直线l的对称点A′,连接BA′交直线l于P.
根据两点之间,线段最短,可知选项D铺设的管道最短.
故选:D.
8.(2018秋?无为县期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
【分析】过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,再根据三角形的面积公式求出CE的长,即为CM+MN的最小值.
【解答】解:过点C作CE⊥AB于点E,交BD于点M′,过点M作MN′⊥BC于N′,
∵BD平分∠ABC,M′E⊥AB于点E,M′N′⊥BC于N
∴M′N′=M′E,
∴CE=CM′+M′E
∴当点M与M′重合,点N与N′重合时,CM+MN的最小值.
∵三角形ABC的面积为8,AB=4,
∴×4?CE=8,
∴CE=4.
即CM+MN的最小值为4.
故选:B.
9.(2018秋?新罗区校级期中)如图,点P为∠AOB内一点,分别作点P关于OA、OB的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为( )
A.16 B.15 C.14 D.13
【分析】根据轴对称的性质可得P1M=PM,P2N=PN,然后根据三角形的周长定义,求出△PMN的周长为P1P2,从而得解.
【解答】解:∵P点关于OB、OA的对称点为P1,P2,
∴P1M=PM,P2N=PN,
∴△PMN的周长=MN+PM+PN=MN+P1M+P2N=P1P2,
∵P1P2=15,
∴△PMN的周长为15.
故选:B.
10.(2018秋?房山区期末)如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.64° C.65° D.70°
【分析】由折叠的性质得到∠D=∠C,再利用外角性质即可求出所求角的度数.
【解答】解:如图,由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:B.
11.(2018秋?汝阳县期末)如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′=AA',则折痕DE的长为( )
A.4 B.3 C.2 D.
【分析】△ABC沿DE折叠,使点A落在点A′处,可得∠DEA=∠DEA′=90°,AE=A′E,所以,△ACB∽△AED,A′为CE的中点,所以,可运用相似三角形的性质求得
【解答】解:∵△ABC沿DE折叠,使点A落在点A′处,
∴∠DEA=∠DEA′=90°,AE=A′E,
∴DE∥BC
∴△ACB∽△AED,
∵CA′=AA',AE=A′E,
∴AE=AC
∵△ACB∽△AED,
∴
即
∴DE=2
故选:C.
12.(2018?辽阳)如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5 B. C.4 D.
【分析】根据题意,作出合适的辅助线,然后根据角平分线的性质、等腰三角形的性质和勾股定理可以求得点B到AC的距离,本题得以解决.
【解答】解:由题意可得,
OC为∠MON的角平分线,
∵OA=OB,OC平分∠AOB,
∴OC⊥AB,
设OC与AB交于点D,作BE⊥AC于点E,
∵AB=6,OA=5,AC=OA,OC⊥AB,
∴AC=5,∠ADC=90°,AD=3,
∴CD=4,
∵,
∴,
解得,BE=,
故选:B.
13.(2018?梧州)如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3 C.4 D.6
【分析】根据角的平分线上的点到角的两边的距离相等即可得.
【解答】解:∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,
∴DE=DF=6,
故选:D.
14.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
【分析】作MN⊥AD于N,根据平行线的性质求出∠DAB,根据角平分线的判定定理得到∠MAB=∠DAB,计算即可.
【解答】解:作MN⊥AD于N,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠DAB=180°﹣∠ADC=70°,
∵DM平分∠ADC,MN⊥AD,MC⊥CD,
∴MN=MC,
∵M是BC的中点,
∴MC=MB,
∴MN=MB,又MN⊥AD,MB⊥AB,
∴∠MAB=∠DAB=35°,
故选:B.
15.(2018秋?开封期中)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②AC=4BF;③DB=DC;④AD⊥BC,其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据等腰三角形的性质三线合一得到BD=CD,AD⊥BC,故③④正确;通过△CDE≌△DBF,得到DE=DF,CE=BF,故①正确,由AE=2BF,得到AC=3BF,故②错误.
【解答】解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故③④正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA),
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故②错误.
故选:B.
16.(2018秋?巴南区期中)如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据角平分线的判定定理解答即可.
【解答】解:根据角平分线的判定定可知,可供选择的站址分别是∠EGB和∠DNA的平分线的交点,
∠AGF和∠CME的平分线的交点,∠FMD和∠BNC的平分线的交点,∠EMD和∠ANC的平分线的交点,
∴可供选择的站址最多有4个,
故选:A.
17.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
【分析】根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质得到∠DAC=∠C,根据三角形内角和定理求出∠BAC,计算即可.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=25°,
∵∠B=60°,∠C=25°,
∴∠BAC=95°,
∴∠BAD=∠BAC﹣∠DAC=70°,
故选:B.
18.(2018秋?江门期末)如图,DE是△ABC中AC边的垂直平分线,若BC=6cm,AB=8cm,则△EBC的周长为( )
A.14cm B.18cm C.20cm D.22cm
【分析】先根据线段垂直平分线的性质得出AE=CE,故CE+BE=AB,再由△EBC的周长=BC+CE+BE=BC+AB即可得出结论.
【解答】解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴CE+BE=AB=8cm.
∵BC=6cm,
∴△EBC的周长=BC+CE+BE=BC+AB=6+8=14(cm).
故选:A.
19.(2018秋?南关区期末)如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
【分析】由直线EM为线段AB的垂直平分线,根据线段垂直平分线定理:可得AM=BM,同理可得BN=NC,然后表示出三角形BMN的三边之和,等量代换可得其周长等于AC的长;
【解答】解:∵直线ME为线段AB的垂直平分线,
∴MA=MB(线段垂直平分线上的点到线段两端点的距离相等),
又直线NF为线段BC的垂直平分线,
∴NB=NC(线段垂直平分线上的点到线段两端点的距离相等),
∴△BMN的周长=BM+MN+BN=AM+MN+NC=AC=24(等量代换),
故选:B.
20.(2018秋?长春期末)如图,在△ABC中,边AC的垂直平分线交边AB于点D,连结CD.若∠A=50°,则∠BDC的大小为( )
A.90° B.100° C.120° D.130°
【分析】根据线段垂直平分线的性质得出AD=DC,推出∠A=∠ACD=50°,根据三角形外角的性质得出即可.
【解答】解:∵△ABC的边AC的垂直平分线DE交边AB于点D,交边AC于点E,
∴AD=DC,
∴∠A=∠ACD,
∵∠A=50°,
∴∠ACD=50°,
∴∠BDC=∠A+∠ACD=50°+50°=100°,
故选:B.
21.(2018秋?雨花区校级期中)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC长为12cm,BE长为8cm,则EC的长为( )
A.8cm B.6cm C.4cm D.2cm
【分析】根据线段垂直平分线上的点到线段两端点的距离相等可以得到AE=BE,进而解答即可.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE,
∵AC=12cm,BE=8cm,
∴EC=AC﹣AE=AC﹣BE=12﹣8=4cm,
故选:C.
22.(2018?兰州)如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
【分析】直接利用平行线的性质结合等腰三角形的性质得出∠2的度数.
【解答】解:∵AB∥CD,
∴∠1=∠ACD=65°,
∵AD=CD,
∴∠DCA=∠CAD=65°,
∴∠2的度数是:180°﹣65°﹣65°=50°.
故选:A.
23.(2018?湖州)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
【分析】先根据等腰三角形的性质以及三角形内角和定理求出∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.再利用角平分线定义即可得出∠ACE=∠ACB=35°.
【解答】解:∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
故选:B.
24.(2018秋?江门期末)等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
【分析】由于长为4的边可能为腰,也可能为底边,故应分两种情况讨论.
【解答】解:当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形
∴其它两边长分别为7,7.
故选:B.
25.(2018秋?顺义区期末)等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
【分析】设顶角的度数为x,表示出底角的度数.根据三角形内角和定理列方程求解.
【解答】解:设顶角的度数为x,则底角的度数为(x﹣30°).
根据题意,得x+2(x﹣30°)=180°,
解得x=80°.
故选:C.
26.(2018秋?朝阳区期末)如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
A.∠ACD=2∠A B.∠A=2∠P C.BP⊥AC D.BC=CP
【分析】根据等腰三角形的性质得到∠ACD=∠A+∠ABC=2∠A,故A正确;根据角平分线的性质得到∠PBC=∠ABC,∠PCD=∠ACD,根据三角形的外角的性质即可得到∠A=2∠P,故B正确;由于∠A≠∠ACB,无法判断BP⊥AC,故C错误;根据等量代换得到∠P=∠PBC,根据等腰三角形的性质得到BC=CP,故D正确.
【解答】解:∵AC=BC,
∴∠A=∠ABC,
∴∠ACD=∠A+∠ABC=2∠A,故A正确;
∵∠ABC与∠ACD的平分线相交于点P,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∴∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,
∴ACD=A+∠ABC=∠P+∠PBC=∠P+PBC,
∴∠A=2∠P,故B正确;
∵∠A≠∠ACB,
∴无法判断BP⊥AC,故C错误;
∵∠PBC=∠ABC,∵∠P=∠A,
∵∠A=∠ABC,
∴∠P=∠PBC,
∴BC=CP,故D正确,
故选:C.
一.选择题
1.(2018?资阳)下列图形具有两条对称轴的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正方形
2.(2018?湘西州)下列四个图形中,是轴对称图形的是( )
A. B. C. D.
3.(2018?苏州)下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
4.(2018?宜昌)如下字体的四个汉字中,是轴对称图形的是( )
A. B. C. D.
5.(2018秋?新罗区校级期中)如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中,错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB,A′B′的交点不一定在直线MN上
6.(2018秋?宜兴市期中)如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=α,则∠ACB的度数为( )
A.α B.90°﹣α C.45° D.α﹣45°
7.(2018秋?石景山区期末)如图,直线l表示一条河,点A,B表示两个村庄,想在直线l上的某点P处修建一个水泵站向A,B两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是( )
A. B.
C. D.
8.(2018秋?无为县期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
9.(2018秋?新罗区校级期中)如图,点P为∠AOB内一点,分别作点P关于OA、OB的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为( )
A.16 B.15 C.14 D.13
10.(2018秋?房山区期末)如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.64° C.65° D.70°
11.(2018秋?汝阳县期末)如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′=AA',则折痕DE的长为( )
A.4 B.3 C.2 D.
12.(2018?辽阳)如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5 B. C.4 D.
13.(2018?梧州)如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3 C.4 D.6
14.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
15.(2018秋?开封期中)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②AC=4BF;③DB=DC;④AD⊥BC,其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
16.(2018秋?巴南区期中)如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有( )
A.4个 B.3个 C.2个 D.1个
17.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
18.(2018秋?江门期末)如图,DE是△ABC中AC边的垂直平分线,若BC=6cm,AB=8cm,则△EBC的周长为( )
A.14cm B.18cm C.20cm D.22cm
19.(2018秋?南关区期末)如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
20.(2018秋?长春期末)如图,在△ABC中,边AC的垂直平分线交边AB于点D,连结CD.若∠A=50°,则∠BDC的大小为( )
A.90° B.100° C.120° D.130°
21.(2018秋?雨花区校级期中)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC长为12cm,BE长为8cm,则EC的长为( )
A.8cm B.6cm C.4cm D.2cm
22.(2018?兰州)如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
23.(2018?湖州)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
24.(2018秋?江门期末)等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
25.(2018秋?顺义区期末)等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
26.(2018秋?朝阳区期末)如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
A.∠ACD=2∠A B.∠A=2∠P C.BP⊥AC D.BC=CP
北师大版数学七下第五章生活中的轴对称复习题---选择题
参考答案与试题解析
一.选择题
1.(2018?资阳)下列图形具有两条对称轴的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正方形
【分析】根据轴对称及对称轴的定义,结合所给图形即可作出判断.
【解答】解:A、等边三角形由3条对称轴,故本选项错误;
B、平行四边形无对称轴,故本选项错误;
C、矩形有2条对称轴,故本选项正确;
D、正方形有4条对称轴,故本选项错误;
故选:C.
2.(2018?湘西州)下列四个图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念求解.
【解答】解:D选项的图形是轴对称图形,A,B,C选项的图形不是轴对称图形.
故选:D.
3.(2018?苏州)下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
【分析】根据轴对称的概念对各选项分析判断利用排除法求解.
【解答】解:A、是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项正确;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:B.
4.(2018?宜昌)如下字体的四个汉字中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的定义逐个判断即可.
【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意;
故选:D.
5.(2018秋?新罗区校级期中)如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中,错误的是( )
A.△AA′P是等腰三角形
B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等
D.直线AB,A′B′的交点不一定在直线MN上
【分析】据对称轴的定义,△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,可以判断出图中各点或线段之间的关系.
【解答】解:∵△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,
∴△AA′P是等腰三角形,MN垂直平分AA′,CC′,这两个三角形的面积相等,故A、B、C选项正确,
直线AB,A′B′关于直线MN对称,因此交点一定在MN上,故D错误,
故选:D.
6.(2018秋?宜兴市期中)如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=α,则∠ACB的度数为( )
A.α B.90°﹣α C.45° D.α﹣45°
【分析】连接AB',BB',过A作AE⊥CD于E,依据∠BAC=∠B'AC,∠DAE=∠B'AE,即可得出∠CAE=∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=∠ACB'=90°﹣∠BAD.
【解答】解:如图,连接AB',BB',过A作AE⊥CD于E,
∵点B关于AC的对称点B'恰好落在CD上,
∴AC垂直平分BB',
∴AB=AB',
∴∠BAC=∠B'AC,
∵AB=AD,
∴AD=AB',
又∵AE⊥CD,
∴∠DAE=∠B'AE,
∴∠CAE=∠BAD=,
又∵∠AEB'=∠AOB'=90°,
∴四边形AOB'E中,∠EB'O=180°﹣,
∴∠ACB'=∠EB'O﹣∠COB'=180°﹣﹣90°=90°﹣,
∴∠ACB=∠ACB'=90°﹣,
故选:B.
7.(2018秋?石景山区期末)如图,直线l表示一条河,点A,B表示两个村庄,想在直线l上的某点P处修建一个水泵站向A,B两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是( )
A. B.
C. D.
【分析】依据轴对称的性质,通过等线段代换,将所求路线长转化为两点之间的距离即可.
【解答】解:作点A关于直线l的对称点A′,连接BA′交直线l于P.
根据两点之间,线段最短,可知选项D铺设的管道最短.
故选:D.
8.(2018秋?无为县期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
【分析】过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,再根据三角形的面积公式求出CE的长,即为CM+MN的最小值.
【解答】解:过点C作CE⊥AB于点E,交BD于点M′,过点M作MN′⊥BC于N′,
∵BD平分∠ABC,M′E⊥AB于点E,M′N′⊥BC于N
∴M′N′=M′E,
∴CE=CM′+M′E
∴当点M与M′重合,点N与N′重合时,CM+MN的最小值.
∵三角形ABC的面积为8,AB=4,
∴×4?CE=8,
∴CE=4.
即CM+MN的最小值为4.
故选:B.
9.(2018秋?新罗区校级期中)如图,点P为∠AOB内一点,分别作点P关于OA、OB的对称点P1,P2,连接P1P2交OB于M,交OA于N,P1P2=15,则△PMN的周长为( )
A.16 B.15 C.14 D.13
【分析】根据轴对称的性质可得P1M=PM,P2N=PN,然后根据三角形的周长定义,求出△PMN的周长为P1P2,从而得解.
【解答】解:∵P点关于OB、OA的对称点为P1,P2,
∴P1M=PM,P2N=PN,
∴△PMN的周长=MN+PM+PN=MN+P1M+P2N=P1P2,
∵P1P2=15,
∴△PMN的周长为15.
故选:B.
10.(2018秋?房山区期末)如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.64° C.65° D.70°
【分析】由折叠的性质得到∠D=∠C,再利用外角性质即可求出所求角的度数.
【解答】解:如图,由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:B.
11.(2018秋?汝阳县期末)如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′=AA',则折痕DE的长为( )
A.4 B.3 C.2 D.
【分析】△ABC沿DE折叠,使点A落在点A′处,可得∠DEA=∠DEA′=90°,AE=A′E,所以,△ACB∽△AED,A′为CE的中点,所以,可运用相似三角形的性质求得
【解答】解:∵△ABC沿DE折叠,使点A落在点A′处,
∴∠DEA=∠DEA′=90°,AE=A′E,
∴DE∥BC
∴△ACB∽△AED,
∵CA′=AA',AE=A′E,
∴AE=AC
∵△ACB∽△AED,
∴
即
∴DE=2
故选:C.
12.(2018?辽阳)如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A.5 B. C.4 D.
【分析】根据题意,作出合适的辅助线,然后根据角平分线的性质、等腰三角形的性质和勾股定理可以求得点B到AC的距离,本题得以解决.
【解答】解:由题意可得,
OC为∠MON的角平分线,
∵OA=OB,OC平分∠AOB,
∴OC⊥AB,
设OC与AB交于点D,作BE⊥AC于点E,
∵AB=6,OA=5,AC=OA,OC⊥AB,
∴AC=5,∠ADC=90°,AD=3,
∴CD=4,
∵,
∴,
解得,BE=,
故选:B.
13.(2018?梧州)如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3 C.4 D.6
【分析】根据角的平分线上的点到角的两边的距离相等即可得.
【解答】解:∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,
∴DE=DF=6,
故选:D.
14.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
【分析】作MN⊥AD于N,根据平行线的性质求出∠DAB,根据角平分线的判定定理得到∠MAB=∠DAB,计算即可.
【解答】解:作MN⊥AD于N,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠DAB=180°﹣∠ADC=70°,
∵DM平分∠ADC,MN⊥AD,MC⊥CD,
∴MN=MC,
∵M是BC的中点,
∴MC=MB,
∴MN=MB,又MN⊥AD,MB⊥AB,
∴∠MAB=∠DAB=35°,
故选:B.
15.(2018秋?开封期中)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②AC=4BF;③DB=DC;④AD⊥BC,其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据等腰三角形的性质三线合一得到BD=CD,AD⊥BC,故③④正确;通过△CDE≌△DBF,得到DE=DF,CE=BF,故①正确,由AE=2BF,得到AC=3BF,故②错误.
【解答】解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故③④正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA),
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故②错误.
故选:B.
16.(2018秋?巴南区期中)如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据角平分线的判定定理解答即可.
【解答】解:根据角平分线的判定定可知,可供选择的站址分别是∠EGB和∠DNA的平分线的交点,
∠AGF和∠CME的平分线的交点,∠FMD和∠BNC的平分线的交点,∠EMD和∠ANC的平分线的交点,
∴可供选择的站址最多有4个,
故选:A.
17.(2018?黄冈)如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
【分析】根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质得到∠DAC=∠C,根据三角形内角和定理求出∠BAC,计算即可.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=25°,
∵∠B=60°,∠C=25°,
∴∠BAC=95°,
∴∠BAD=∠BAC﹣∠DAC=70°,
故选:B.
18.(2018秋?江门期末)如图,DE是△ABC中AC边的垂直平分线,若BC=6cm,AB=8cm,则△EBC的周长为( )
A.14cm B.18cm C.20cm D.22cm
【分析】先根据线段垂直平分线的性质得出AE=CE,故CE+BE=AB,再由△EBC的周长=BC+CE+BE=BC+AB即可得出结论.
【解答】解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴CE+BE=AB=8cm.
∵BC=6cm,
∴△EBC的周长=BC+CE+BE=BC+AB=6+8=14(cm).
故选:A.
19.(2018秋?南关区期末)如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
【分析】由直线EM为线段AB的垂直平分线,根据线段垂直平分线定理:可得AM=BM,同理可得BN=NC,然后表示出三角形BMN的三边之和,等量代换可得其周长等于AC的长;
【解答】解:∵直线ME为线段AB的垂直平分线,
∴MA=MB(线段垂直平分线上的点到线段两端点的距离相等),
又直线NF为线段BC的垂直平分线,
∴NB=NC(线段垂直平分线上的点到线段两端点的距离相等),
∴△BMN的周长=BM+MN+BN=AM+MN+NC=AC=24(等量代换),
故选:B.
20.(2018秋?长春期末)如图,在△ABC中,边AC的垂直平分线交边AB于点D,连结CD.若∠A=50°,则∠BDC的大小为( )
A.90° B.100° C.120° D.130°
【分析】根据线段垂直平分线的性质得出AD=DC,推出∠A=∠ACD=50°,根据三角形外角的性质得出即可.
【解答】解:∵△ABC的边AC的垂直平分线DE交边AB于点D,交边AC于点E,
∴AD=DC,
∴∠A=∠ACD,
∵∠A=50°,
∴∠ACD=50°,
∴∠BDC=∠A+∠ACD=50°+50°=100°,
故选:B.
21.(2018秋?雨花区校级期中)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC长为12cm,BE长为8cm,则EC的长为( )
A.8cm B.6cm C.4cm D.2cm
【分析】根据线段垂直平分线上的点到线段两端点的距离相等可以得到AE=BE,进而解答即可.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE,
∵AC=12cm,BE=8cm,
∴EC=AC﹣AE=AC﹣BE=12﹣8=4cm,
故选:C.
22.(2018?兰州)如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
【分析】直接利用平行线的性质结合等腰三角形的性质得出∠2的度数.
【解答】解:∵AB∥CD,
∴∠1=∠ACD=65°,
∵AD=CD,
∴∠DCA=∠CAD=65°,
∴∠2的度数是:180°﹣65°﹣65°=50°.
故选:A.
23.(2018?湖州)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
【分析】先根据等腰三角形的性质以及三角形内角和定理求出∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.再利用角平分线定义即可得出∠ACE=∠ACB=35°.
【解答】解:∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
故选:B.
24.(2018秋?江门期末)等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
【分析】由于长为4的边可能为腰,也可能为底边,故应分两种情况讨论.
【解答】解:当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形
∴其它两边长分别为7,7.
故选:B.
25.(2018秋?顺义区期末)等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
【分析】设顶角的度数为x,表示出底角的度数.根据三角形内角和定理列方程求解.
【解答】解:设顶角的度数为x,则底角的度数为(x﹣30°).
根据题意,得x+2(x﹣30°)=180°,
解得x=80°.
故选:C.
26.(2018秋?朝阳区期末)如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
A.∠ACD=2∠A B.∠A=2∠P C.BP⊥AC D.BC=CP
【分析】根据等腰三角形的性质得到∠ACD=∠A+∠ABC=2∠A,故A正确;根据角平分线的性质得到∠PBC=∠ABC,∠PCD=∠ACD,根据三角形的外角的性质即可得到∠A=2∠P,故B正确;由于∠A≠∠ACB,无法判断BP⊥AC,故C错误;根据等量代换得到∠P=∠PBC,根据等腰三角形的性质得到BC=CP,故D正确.
【解答】解:∵AC=BC,
∴∠A=∠ABC,
∴∠ACD=∠A+∠ABC=2∠A,故A正确;
∵∠ABC与∠ACD的平分线相交于点P,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∴∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,
∴ACD=A+∠ABC=∠P+∠PBC=∠P+PBC,
∴∠A=2∠P,故B正确;
∵∠A≠∠ACB,
∴无法判断BP⊥AC,故C错误;
∵∠PBC=∠ABC,∵∠P=∠A,
∵∠A=∠ABC,
∴∠P=∠PBC,
∴BC=CP,故D正确,
故选:C.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
