六年级下册数学课件总复习 1.13 练习二十比和比例 西师大版(共16张PPT)
文档属性
| 名称 | 六年级下册数学课件总复习 1.13 练习二十比和比例 西师大版(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 12:17:12 | ||
图片预览




文档简介
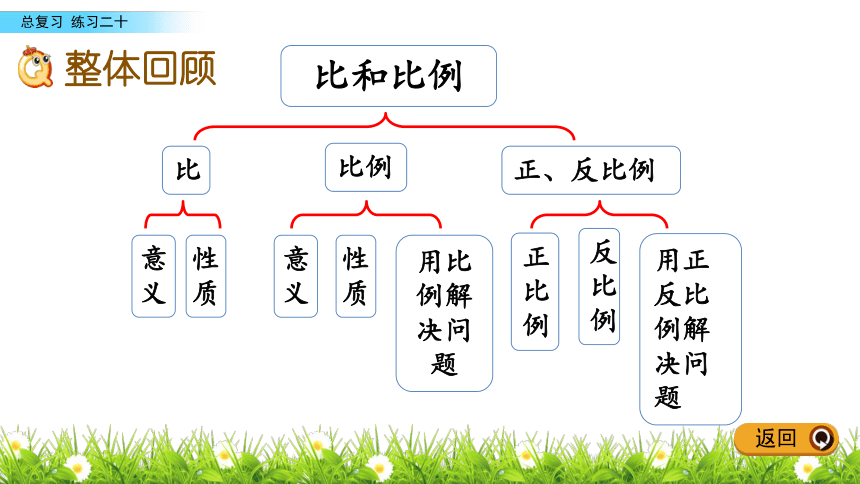
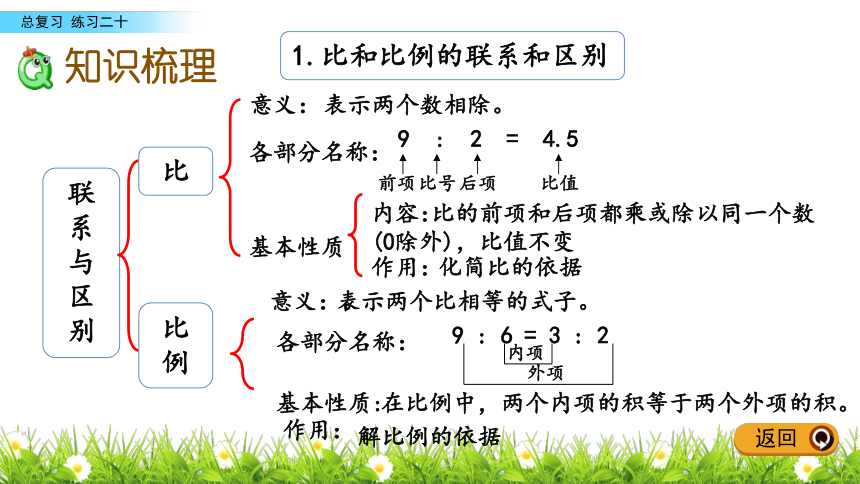
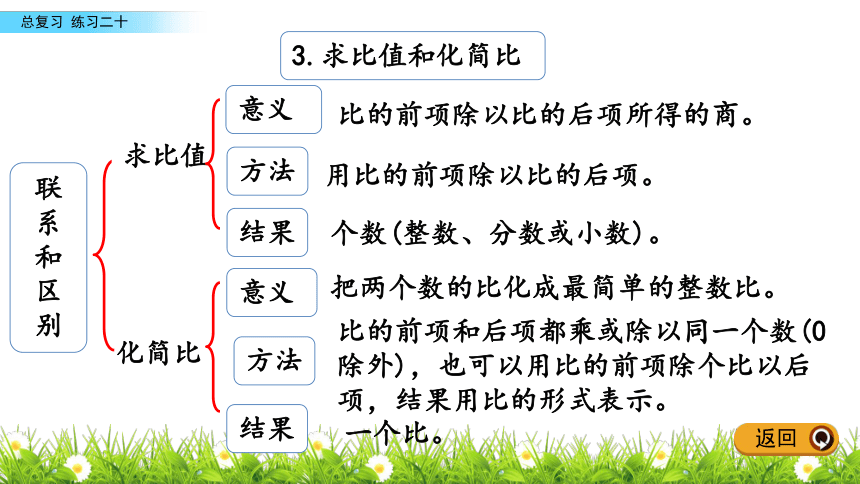
课件16张PPT。练习二十整体回顾综合运用课后作业总复习知识梳理5比和比例比意义性质正比例反比例比例用比例解决问题正、反比例意义性质用正反比例解决问题整体回顾返回意义:1.比和比例的联系和区别联系与区别比比例表示两个比相等的式子。各部分名称:9 : 2 = 4.5基本性质内容:作用:在比例中,两个内项的积等于两个外项的积。作用:表示两个数相除。 比的前项和后项都乘或除以同一个数(0除外),比值不变化简比的依据意义:。各部分名称:基本性质:解比例的依据前项外项比号后项比值9 : 6 = 3 : 2内项知识梳理返回2.比、分数、除法的联系和区别联系和区别联系前项 比分数除法分子被除数比号分数线除号后项分母比值除数分数值商表示数量间的一种关系 比分数除法一种数一种运算区别返回比的前项除以比的后项所得的商。3.求比值和化简比联系和区别求比值意义方法结果化简比意义方法结果用比的前项除以比的后项。个数(整数、分数或小数)。把两个数的比化成最简单的整数比。比的前项和后项都乘或除以同一个数(0除外),也可以用比的前项除个比以后项,结果用比的形式表示。一个比。返回在工农业生产和日常生活中,常常需要把一个数量按4.用比例知识解决问题按比例分配照一定的比进行分配,这种分配通常叫做按比例分配。返回4.用比例知识解决问题(1)已知总数和各部分量的比,求各部分量:①先求出总份数,再求各部分量占总数的几分之几,然②先求出每份是多少,再用每份数乘各部分量所占的份后用总数乘各部分量占总数的几分之几,求出各部分量。数,求出各部分量。返回份数求出其余各部分量。4.用比例知识解决问题(2)已知各部分量的比和某个部分量,求其余各部分量:①设未知的部分量为x,根据各部分量的比列方程解答③求出未知量占已知量的几分之几,用已知量乘未知量占④求出已知量占未知量的几分之几,用已知量除以已知量②先求出每份是多少,再用每份数乘其余各部分量所占的已知量的几分之几,求出未知量。占未知量的几分之几,求出未知量。返回两种相关联的量,一种量变化,
另一种量也随着变化5.正比例和反比例联系相同点正比例反比例两种量中相对应的两个数的比值一定两种量中相对应的两个数的乘积一定一种量扩大(或缩小),另一种量也随着扩大
(或缩小)。一种量变化,量也随着扩大(或缩小)。 =k(一定)不同点正比例反比例变化方向正比例反比例关系式正比例反比例χy=k(一定)返回7.判断正、反比例的方法找,二看,三判断。(1)找变量:分析数量关系,确定哪两种量是相关联的量。(2)看定量:分析这两种相关联的量,它们之间的关系是比值一定还是积一定。(3)判断:如果比值一定,就成正比例;如果积一定,就成反比例;如果比值和积都不是定量,就不成比例返回8.用正、反比例知识解决问题(1)分析数量关系,判断成什么比例。(2)找等量关系。如果是成正比例,则按“等比”找等量
关系;如果是成反比例,则按“等积”找等量关系。(3)列比例。设未知数为x,根据等量关系列出比例。解答
比例应用题的关键。(4)解比例。(5)检验并写出答语。返回判断。(正确的在括号里画“√”,错误的画“×”。)⑴3χ+2>5是方程( )⑵在一个比例中,如果两个内项的积是1,那么两个外项一定互为倒数。( )⑶广州到北京的航线长一定,飞机飞行的速度和时间成反比例。( )⑷每天劳动报酬一定,总收入与工作时间成正比例。( )⑸订阅某一种杂志的数量和金额成反比例。( )×√√××综合运用返回解比例。9:8=x:12 = :=x :解:8x=12×9x=108÷8x=13.5解:0.1x=0.4×35x=14÷0.1x=140解: x= × x= ×8x=5返回机器上有一对互相咬合的齿轮,大齿轮有200个齿每分转20转;小齿轮有50个齿,每分转80转。⑴大、小齿轮齿数比是( ):( )⑵大、小齿轮每分转数的比是( ):( )⑶这两个比能组成比例吗?200502080能组成比例。因为:大齿轮每分转过的齿数:200×20=4000(个) (一定)小齿轮每分转过的齿数:50×80=4000(个) (一定)返回用水泥、河砂和石子按2:3:5的比例配制240吨混凝土,需水泥、河砂和石子各多少吨?240×=240× =96(吨)240×=240× =72(吨)240×=240× =120(吨)答:需水泥、河砂和石子各96吨、72吨、120吨。返回课本:
第80页第2、11、12题课后作业返回
另一种量也随着变化5.正比例和反比例联系相同点正比例反比例两种量中相对应的两个数的比值一定两种量中相对应的两个数的乘积一定一种量扩大(或缩小),另一种量也随着扩大
(或缩小)。一种量变化,量也随着扩大(或缩小)。 =k(一定)不同点正比例反比例变化方向正比例反比例关系式正比例反比例χy=k(一定)返回7.判断正、反比例的方法找,二看,三判断。(1)找变量:分析数量关系,确定哪两种量是相关联的量。(2)看定量:分析这两种相关联的量,它们之间的关系是比值一定还是积一定。(3)判断:如果比值一定,就成正比例;如果积一定,就成反比例;如果比值和积都不是定量,就不成比例返回8.用正、反比例知识解决问题(1)分析数量关系,判断成什么比例。(2)找等量关系。如果是成正比例,则按“等比”找等量
关系;如果是成反比例,则按“等积”找等量关系。(3)列比例。设未知数为x,根据等量关系列出比例。解答
比例应用题的关键。(4)解比例。(5)检验并写出答语。返回判断。(正确的在括号里画“√”,错误的画“×”。)⑴3χ+2>5是方程( )⑵在一个比例中,如果两个内项的积是1,那么两个外项一定互为倒数。( )⑶广州到北京的航线长一定,飞机飞行的速度和时间成反比例。( )⑷每天劳动报酬一定,总收入与工作时间成正比例。( )⑸订阅某一种杂志的数量和金额成反比例。( )×√√××综合运用返回解比例。9:8=x:12 = :=x :解:8x=12×9x=108÷8x=13.5解:0.1x=0.4×35x=14÷0.1x=140解: x= × x= ×8x=5返回机器上有一对互相咬合的齿轮,大齿轮有200个齿每分转20转;小齿轮有50个齿,每分转80转。⑴大、小齿轮齿数比是( ):( )⑵大、小齿轮每分转数的比是( ):( )⑶这两个比能组成比例吗?200502080能组成比例。因为:大齿轮每分转过的齿数:200×20=4000(个) (一定)小齿轮每分转过的齿数:50×80=4000(个) (一定)返回用水泥、河砂和石子按2:3:5的比例配制240吨混凝土,需水泥、河砂和石子各多少吨?240×=240× =96(吨)240×=240× =72(吨)240×=240× =120(吨)答:需水泥、河砂和石子各96吨、72吨、120吨。返回课本:
第80页第2、11、12题课后作业返回
