探索图形(11张PPT)
图片预览



文档简介
长方体和正方体
探索图形
学习目标
1.根据正方体的特征,利用学具找到每种涂色情况的小正方体的数量,确定每种涂色情况的小正方体的位置规律。
2.在探究体验的过程中发现图形的规律。
重点
找出并发现图形中蕴涵的规律。
难点
正确数出每种涂色的小正方体的个数。
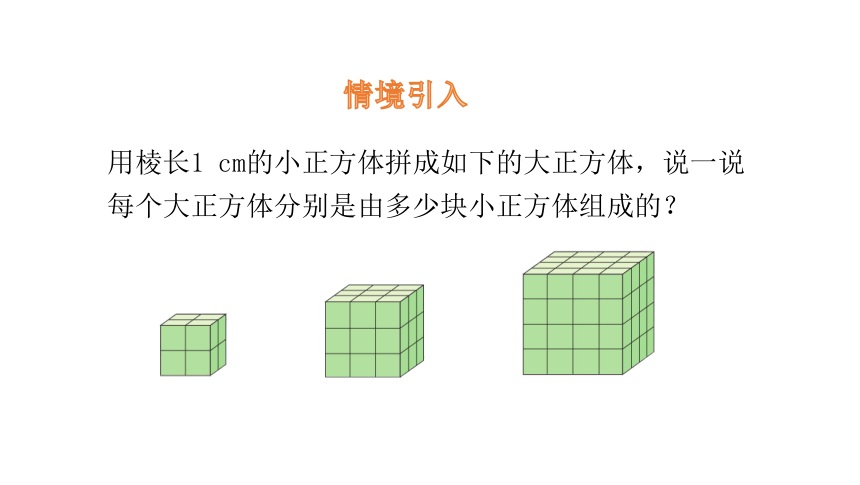
情境引入
用棱长1 cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
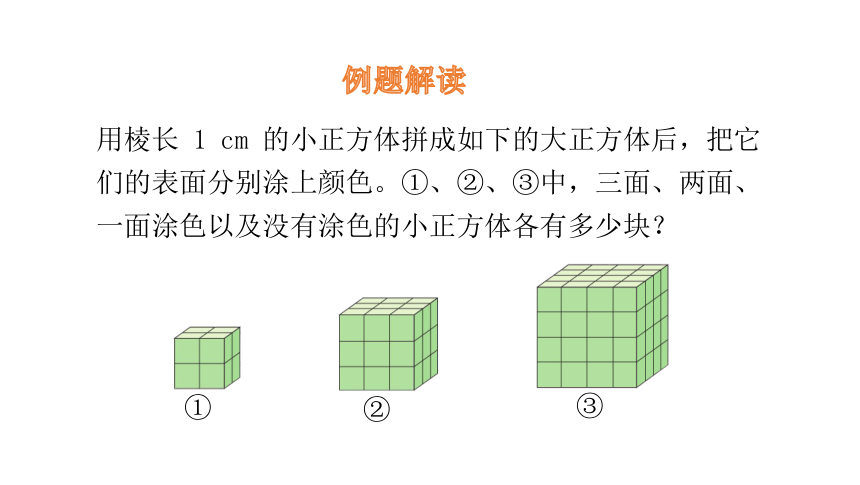
例题解读
用棱长 1 cm 的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
? 8 0 0 0
? 8 12 6 1
? 8 24
?
?
24
8
8
36
54
27
8
48
96
64
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
①
②
③
④
⑤
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
? 8 0 0 0
? 8 12 6 1
? 8 24
?
?
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
观察上表,你能发现什么?
在顶点位置的正方体露出 3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
?
?
?
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8 0 0 0
8 12 6 1
8 24
24
8
8
36
54
27
8
48
96
64
8
60
150
125
8
72
216
216
8
84
294
343
①
②
③
④
⑤
⑥
⑦
⑧
4
10
20
如果摆成下面的几何体,你会数吗?
绿卡图书—走向成功的通行证
探索图形
学习目标
1.根据正方体的特征,利用学具找到每种涂色情况的小正方体的数量,确定每种涂色情况的小正方体的位置规律。
2.在探究体验的过程中发现图形的规律。
重点
找出并发现图形中蕴涵的规律。
难点
正确数出每种涂色的小正方体的个数。
情境引入
用棱长1 cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
例题解读
用棱长 1 cm 的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
? 8 0 0 0
? 8 12 6 1
? 8 24
?
?
24
8
8
36
54
27
8
48
96
64
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
①
②
③
④
⑤
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
? 8 0 0 0
? 8 12 6 1
? 8 24
?
?
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
观察上表,你能发现什么?
在顶点位置的正方体露出 3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
?
?
?
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8 0 0 0
8 12 6 1
8 24
24
8
8
36
54
27
8
48
96
64
8
60
150
125
8
72
216
216
8
84
294
343
①
②
③
④
⑤
⑥
⑦
⑧
4
10
20
如果摆成下面的几何体,你会数吗?
绿卡图书—走向成功的通行证
