六年级上册数学第三单元一课一练-3.3探索规律 西师大版(2014秋)(含答案)
文档属性
| 名称 | 六年级上册数学第三单元一课一练-3.3探索规律 西师大版(2014秋)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 21:05:51 | ||
图片预览



文档简介
六年级上册数学一课一练-3.3探索规律
一、单选题
1.5÷7的商用循环小数表示,这个小数的小数点后面第150位数字是( )
A.?1 ???????????????????????????????????????B.?2 ???????????????????????????????????????C.?5 ???????????????????????????????????????D.?7
2.如果37037×3=111111
37037×6=222222
37037×9=333333,
那么37037×12=(??? )。
A.?444444??????????????????????????????B.?666666??????????????????????????????C.?888888??????????????????????????????D.?999999
3.4÷11商的小数点后面第100位数字是( )
A.?0 ???????????????????????????????????????B.?3 ???????????????????????????????????????C.?7 ???????????????????????????????????????D.?6
4.5÷7的商用循环小数表示,这个小数的小数点后面第200位数字是( )
A.?7???? ?????????????????????????????????????B.?1 ?????????????????????????????????????C.?2?? ?????????????????????????????????????D.?5
5.3.40. 小数点后的第30位上的数字是( )
A.?1 ???????????????????????????????????????B.?4 ???????????????????????????????????????C.?2 ???????????????????????????????????????D.?0
6.一组数1,3,4,7,11,18,从第三个数起后面一个数是前面两个数的和,那么第5555个数除以5,余数是几?( )
A.?2 ???????????????????????????????????????B.?3 ???????????????????????????????????????C.?4 ???????????????????????????????????????D.?5
7.加法算式1+2,2+5,3+8,1+11,2+14,3+17,……是按一定规律排列的,则第40个加法算式是(??? )。
A.?1+120????????????????????????????????B.?2+119????????????????????????????????C.?1+199????????????????????????????????D.?2+120
二、填空题
8.将 化为小数,小数点后第100个数字是________.
9.9876-6789=3087;
6543-3456=3087;
3210-123=3087;
7654-4567=________
10.已知1+3=22=4;1+3+5=32=9;那么1+3+5+7+9+11+……+99=________。
11.2003名学生从前往后排成一列,按下面的规则报数,如果某个同学报的数是一位数,后面的同学就在报出这个数与9的和,如果某个同学报的数是二位数,后面的同学就要报出这个数的个位数与6的和,现让第一个同学报2,那么最后一个同学所报的数是________?.
12.循环小数0.285714,它的小数点后的第2001位数字是________?.
13.现在1克、2克、4克、8克、16克砝码各一个,称东西时,砝码只能放在天平的一边,可以称出________种不同的重量。
14.要使算式+++++++++□=1成立,则□中的数等于________?.
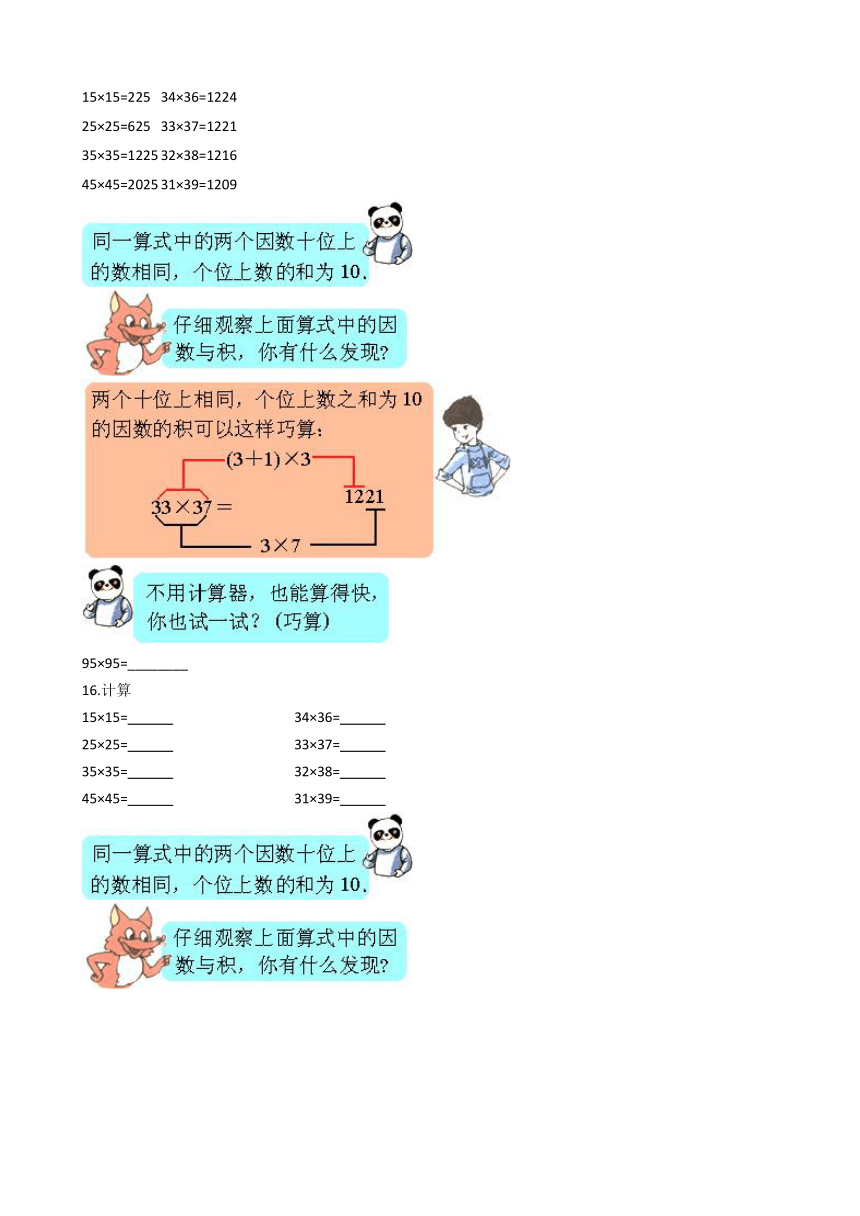
15.计算
15×15=225
34×36=1224
25×25=625
33×37=1221
35×35=1225
32×38=1216
45×45=2025
31×39=1209
95×95=________
16.计算
15×15= 34×36=
25×25= 33×37=
35×35= 32×38=
45×45= 31×39=
65×65=________
三、计算题
17.化为小数后,小数点后面第2013位上的数字是几?这2013个数字的和是多少?
18.把分数化成小数后,小数点后面第2005位上的数字是多少?
四、解答题
19.数一数,填一填 ??? 想一想,每次少几个?
20.先找出下面各式的规律,再按规律写等式。
? ÷3= -3?????????? ÷4= -4
÷5= -5 ?????? ÷6= -6
五、综合题
21.按规律填数。
(1)2,5,8,11,________,________。
(2), , , ,________,________。
六、应用题
22.数一数,填一填,想一想 每次增加多少个?
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】解:5÷7=0.1428,
循环节是714285六个数字;
150÷6=25(个),
所以第150位数字是第25个循环节的最后一个数字,是5.
故选:5.
【分析】把5÷7=0.1428, 这个小数的循环节是714285,有6位数,150÷6=25(个,所以小数部分的第150位数字是25的最后一个数字是5,据此解答.
2.【答案】A
【解析】【解答】解:根据规律可知,37037×12=444444 故答案为:A
【分析】根据前面三题找出计算规律,第一个因数不变,第二个因数依次增加3,积是六位数,每个数字都相同,由此根据规律直接写出得数即可.
3.【答案】D
【解析】【解答】解:4÷11=0., 因为循环节2位,所以100÷2=50,因此小数点右边第100位上的数字是6.
故选:D.
【分析】先计算4÷11=0., 因为循环节2位,所以100÷2=50,没有余数,因此小数点右边第100位上的数字是6.
4.【答案】B
【解析】【解答】解:5÷7=0.1428,
循环节是714285六个数字;
200÷6=33…2,
所以小数部分的第200位数字是与第2个数字相同,都是1,
故选:B.
【分析】把5÷7=这个小数的循环节是714285,有6位数,200÷6=33…2,所以小数部分的第200位数字是34的第二个数字是1,据此解答.
5.【答案】B
【解析】【解答】解:30÷4=7…2,
循环节第二个数字是4,所以小数点后的第30位上的数字就是4.
故选:B.
【分析】3.40的循环节是1402,有4位数字,用30除以4,余数是几,就是循环节的第几个数字,没有余数就是循环节的最后一个数字,据此解答.
6.【答案】C
【解析】【解答】解:一串数是:1,3,4,7,11,18,29、47、76、123、199、…
这此数除以5的余数是:1、3、4、2;1、3、4、2;1、3、4、2、…
余数中每4个数为一循环,循环1、3、4、2,
5555÷4=1388…3,
所以第5555个数除以5余数为4.
故选:C.
【分析】由题意知:这串数的规律是1,3,4,7,11,18,…从第三个数是前面两个数的和,计算这些数除以5的余数,找出规律:每4个为一循环,用5555除以5,看看有多少个循环,余数是几则看循环数里第几个数,是几就余几.
7.【答案】C
【解析】【解答】解:40÷3=13……1,第一个加数是“1、2、3”中的第一个是1; 第二个加数: 2+(40-1)×3 =2+117 =119 所以第40个加法算式是1+119 故答案为:C
【分析】第一个加数是“1、2、3”三个数字循环,用40除以3求出商和余数,余数是几就说明第40个算式中的第一个加数与“1、2、3”中的第几个数字相同;第二个加数依次多3,第40个算式中第二个加数比2多(40-1)个3,由此计算出第二个加数即可。
二、填空题
8.【答案】8
【解析】【解答】解: =0. 4285?, 100÷6=16…4,根据余数推断小数点后第100位上的数字是8. 故答案为:8. 【分析】?用分子除以分母得循环小数商为0. 4285 ,循环节为6位数,要看小数点后第一百位上的数字是几,就看100除以6的余数是几.据此解答.
9.【答案】3087
【解析】【解答】7654-4567=3087 故答案为:3087
【分析】观察所给算式可以看出:被减数和减数是由四个连续自然数组成的最大数和最小数,不管这几个数字是多少,它们的差都是3087。
10.【答案】502=2500
【解析】【解答】解:1到99共有50个数字,所以算式的得数就是502=2500. 故答案为:502;2500 【分析】规律:算式中都是相邻的奇数,得数=数字个数×数字个数,按照这个规律计算即可,注意要判断出1到99中共有几个奇数.
11.【答案】15
【解析】【解答】解:因为从第二名开始循环,每一个循环占13名同学,报数分别为11、7、16、12、8、17、13、9、18、14、10、6、15, 所以 ÷13=154, 对应的一个循环中的第13个数是15, 故答案为:15. 【分 析】只分析前几位同学报的数就可以发现规律:第一名同学报2,第二名同学报2+9=11,第三名同学报1+6=7,第四名同学报7+9=16,第五名同学 报6+6=12,第六名同学报2+6=8,第七名同学报8+9=17,第八名同学报7+6=13,第九名同学报3+6=9,第十名同学报9+9=18,第 十一名同学报8+6=14,第十二名同学报4+6=10,第十三名同学报0+6=6,第十四名同学报6+9=15,第十五名同学报5+6=11,第十六名 同学报1+6=7…依次算下去,分别报数为2、11、7、16、12、8、17、13、9、18、14、10、6、15、11、7…其实我们不难发现除了 第一个数2外,是11、7、16、12、8、17、13、9、18、14、10、6、15这13个数为一个循环,即从第二名开始循环,每一个循环占13名 同学,所以 ÷13看余数是几就是对应的一个循环中的第几个数.
12.【答案】5
【解析】【解答】解:0.8571是按照285714六位进行循环的; 2001÷6=333…3; 余数是3,第2001位就和第3位相同是5. 故答案为:5. 【分析】0.8571是按照285714六位进行循环的,求出2001里面有多少个这样的循环节,还余几个数字,再根据余数判断即可.
13.【答案】31
【解析】【解答】31种, 可称1克~31克中的任何一个重量, 此题为组合题, 5个砝码选1个有5种, 5选2有10种, 5选3有10种, 5选4有4种, 5选5有1种, 合计31种。 故答案为: 31。 【分析】这是组合题目,分别找出选1到5个砝码各有几种组合,然后相加即可。
14.【答案】
【解析】【解答】解:++++++++, =+-+-+···+-, =1﹣, =. □=1﹣, =. 【分析】因为++++++++□=1,所以□=1﹣(+-+-+···+-),括号内的分数可以简算.
15.【答案】9025
【解析】【解答】解:95×95=9025 故答案为:9025 【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
16.【答案】4225
【解析】【解答】解:65×65=4225 故答案为:4225
【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
三、计算题
17.【答案】解:=2÷7=0.285714275714… 2013÷6=335…3, 循环节中第三个数是5, (2+7+5+7+1+4)×335+2+7+5 =26×335+14 =8710+14 =8724 答:小数点后面第2013位上的数字是5; 这2013个数字的和是8724.
【解析】【分析】2÷7是一个循环小数,循环节是285714,看2013由多少个循环节零几个数即可判断. 一组的和是2+7+5+7+1+4=26,共几组,就用几乘26,最后再加2加7加5即可.
18.【答案】解:=0.9230, 循环节是692307有6个数字, 2005÷6=334(个)…1, 所以第2005位上是第335个循环节的第1位数字,是6. 答:小数点后面第2005位上的数字是6.
【解析】【分析】因为=0.9230该结果是循环小数,它的循环节是692307,是6位数,2005÷6=334(个)…1,所以小数部分的第2005位数字是334个循环节后的335个循环节上的第1个数字,循环节692307的第1个数字是6,据此解答.
四、解答题
19.【答案】每次少2个。
【解析】【解答】由图数得从左到右依次是6、4、2个西瓜,因为6-4=2,4-2=2,所以每次少2个西瓜。 【分析】考查十以内的减法计算以及读图做题的能力。
20.【答案】÷7= -7??? ÷8= -8
【解析】【分析】先观察四个算式的特征,然后判断规律,被除数是分数,除数是整数,分母比除数小1,分子是除数与除数的乘积,得数是这个分数减去这个整数,按照这样的规律写出两个算式即可。
五、综合题
21.【答案】(1)14;17 (2);
【解析】【解答】(1)2+3=5,5+3=8,8+3=11,11+3=14,14+3=17 (2)=, =, =, =, =, = 故答案为:14;17; ? ;
【分析】(1)根据观察可知,前一项+3=后一项,代入计算即可得出答案。 (2)分母:n2 , 分子:n2-1(n从2开始到7),将对应数字代入即可求出结果。
六、应用题
22.【答案】解:通过数数的方法,在括号中填上相应小象的个数,分别是1、4、7,将中间一组的小象排除一个,数一数剩下的个数,就为增加的个数,由图知,增加了3个;以 相同的方法,将第三组小象排除4个,数剩下的个数,为3个,也是增加了3个。所以每次增加了3个小象。也可通过1+3=4,4+3=7,计算出每次增加3 个。
【解析】【分析】考查读图能力和十以内的加法计算。
一、单选题
1.5÷7的商用循环小数表示,这个小数的小数点后面第150位数字是( )
A.?1 ???????????????????????????????????????B.?2 ???????????????????????????????????????C.?5 ???????????????????????????????????????D.?7
2.如果37037×3=111111
37037×6=222222
37037×9=333333,
那么37037×12=(??? )。
A.?444444??????????????????????????????B.?666666??????????????????????????????C.?888888??????????????????????????????D.?999999
3.4÷11商的小数点后面第100位数字是( )
A.?0 ???????????????????????????????????????B.?3 ???????????????????????????????????????C.?7 ???????????????????????????????????????D.?6
4.5÷7的商用循环小数表示,这个小数的小数点后面第200位数字是( )
A.?7???? ?????????????????????????????????????B.?1 ?????????????????????????????????????C.?2?? ?????????????????????????????????????D.?5
5.3.40. 小数点后的第30位上的数字是( )
A.?1 ???????????????????????????????????????B.?4 ???????????????????????????????????????C.?2 ???????????????????????????????????????D.?0
6.一组数1,3,4,7,11,18,从第三个数起后面一个数是前面两个数的和,那么第5555个数除以5,余数是几?( )
A.?2 ???????????????????????????????????????B.?3 ???????????????????????????????????????C.?4 ???????????????????????????????????????D.?5
7.加法算式1+2,2+5,3+8,1+11,2+14,3+17,……是按一定规律排列的,则第40个加法算式是(??? )。
A.?1+120????????????????????????????????B.?2+119????????????????????????????????C.?1+199????????????????????????????????D.?2+120
二、填空题
8.将 化为小数,小数点后第100个数字是________.
9.9876-6789=3087;
6543-3456=3087;
3210-123=3087;
7654-4567=________
10.已知1+3=22=4;1+3+5=32=9;那么1+3+5+7+9+11+……+99=________。
11.2003名学生从前往后排成一列,按下面的规则报数,如果某个同学报的数是一位数,后面的同学就在报出这个数与9的和,如果某个同学报的数是二位数,后面的同学就要报出这个数的个位数与6的和,现让第一个同学报2,那么最后一个同学所报的数是________?.
12.循环小数0.285714,它的小数点后的第2001位数字是________?.
13.现在1克、2克、4克、8克、16克砝码各一个,称东西时,砝码只能放在天平的一边,可以称出________种不同的重量。
14.要使算式+++++++++□=1成立,则□中的数等于________?.
15.计算
15×15=225
34×36=1224
25×25=625
33×37=1221
35×35=1225
32×38=1216
45×45=2025
31×39=1209
95×95=________
16.计算
15×15= 34×36=
25×25= 33×37=
35×35= 32×38=
45×45= 31×39=
65×65=________
三、计算题
17.化为小数后,小数点后面第2013位上的数字是几?这2013个数字的和是多少?
18.把分数化成小数后,小数点后面第2005位上的数字是多少?
四、解答题
19.数一数,填一填 ??? 想一想,每次少几个?
20.先找出下面各式的规律,再按规律写等式。
? ÷3= -3?????????? ÷4= -4
÷5= -5 ?????? ÷6= -6
五、综合题
21.按规律填数。
(1)2,5,8,11,________,________。
(2), , , ,________,________。
六、应用题
22.数一数,填一填,想一想 每次增加多少个?
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】解:5÷7=0.1428,
循环节是714285六个数字;
150÷6=25(个),
所以第150位数字是第25个循环节的最后一个数字,是5.
故选:5.
【分析】把5÷7=0.1428, 这个小数的循环节是714285,有6位数,150÷6=25(个,所以小数部分的第150位数字是25的最后一个数字是5,据此解答.
2.【答案】A
【解析】【解答】解:根据规律可知,37037×12=444444 故答案为:A
【分析】根据前面三题找出计算规律,第一个因数不变,第二个因数依次增加3,积是六位数,每个数字都相同,由此根据规律直接写出得数即可.
3.【答案】D
【解析】【解答】解:4÷11=0., 因为循环节2位,所以100÷2=50,因此小数点右边第100位上的数字是6.
故选:D.
【分析】先计算4÷11=0., 因为循环节2位,所以100÷2=50,没有余数,因此小数点右边第100位上的数字是6.
4.【答案】B
【解析】【解答】解:5÷7=0.1428,
循环节是714285六个数字;
200÷6=33…2,
所以小数部分的第200位数字是与第2个数字相同,都是1,
故选:B.
【分析】把5÷7=这个小数的循环节是714285,有6位数,200÷6=33…2,所以小数部分的第200位数字是34的第二个数字是1,据此解答.
5.【答案】B
【解析】【解答】解:30÷4=7…2,
循环节第二个数字是4,所以小数点后的第30位上的数字就是4.
故选:B.
【分析】3.40的循环节是1402,有4位数字,用30除以4,余数是几,就是循环节的第几个数字,没有余数就是循环节的最后一个数字,据此解答.
6.【答案】C
【解析】【解答】解:一串数是:1,3,4,7,11,18,29、47、76、123、199、…
这此数除以5的余数是:1、3、4、2;1、3、4、2;1、3、4、2、…
余数中每4个数为一循环,循环1、3、4、2,
5555÷4=1388…3,
所以第5555个数除以5余数为4.
故选:C.
【分析】由题意知:这串数的规律是1,3,4,7,11,18,…从第三个数是前面两个数的和,计算这些数除以5的余数,找出规律:每4个为一循环,用5555除以5,看看有多少个循环,余数是几则看循环数里第几个数,是几就余几.
7.【答案】C
【解析】【解答】解:40÷3=13……1,第一个加数是“1、2、3”中的第一个是1; 第二个加数: 2+(40-1)×3 =2+117 =119 所以第40个加法算式是1+119 故答案为:C
【分析】第一个加数是“1、2、3”三个数字循环,用40除以3求出商和余数,余数是几就说明第40个算式中的第一个加数与“1、2、3”中的第几个数字相同;第二个加数依次多3,第40个算式中第二个加数比2多(40-1)个3,由此计算出第二个加数即可。
二、填空题
8.【答案】8
【解析】【解答】解: =0. 4285?, 100÷6=16…4,根据余数推断小数点后第100位上的数字是8. 故答案为:8. 【分析】?用分子除以分母得循环小数商为0. 4285 ,循环节为6位数,要看小数点后第一百位上的数字是几,就看100除以6的余数是几.据此解答.
9.【答案】3087
【解析】【解答】7654-4567=3087 故答案为:3087
【分析】观察所给算式可以看出:被减数和减数是由四个连续自然数组成的最大数和最小数,不管这几个数字是多少,它们的差都是3087。
10.【答案】502=2500
【解析】【解答】解:1到99共有50个数字,所以算式的得数就是502=2500. 故答案为:502;2500 【分析】规律:算式中都是相邻的奇数,得数=数字个数×数字个数,按照这个规律计算即可,注意要判断出1到99中共有几个奇数.
11.【答案】15
【解析】【解答】解:因为从第二名开始循环,每一个循环占13名同学,报数分别为11、7、16、12、8、17、13、9、18、14、10、6、15, 所以 ÷13=154, 对应的一个循环中的第13个数是15, 故答案为:15. 【分 析】只分析前几位同学报的数就可以发现规律:第一名同学报2,第二名同学报2+9=11,第三名同学报1+6=7,第四名同学报7+9=16,第五名同学 报6+6=12,第六名同学报2+6=8,第七名同学报8+9=17,第八名同学报7+6=13,第九名同学报3+6=9,第十名同学报9+9=18,第 十一名同学报8+6=14,第十二名同学报4+6=10,第十三名同学报0+6=6,第十四名同学报6+9=15,第十五名同学报5+6=11,第十六名 同学报1+6=7…依次算下去,分别报数为2、11、7、16、12、8、17、13、9、18、14、10、6、15、11、7…其实我们不难发现除了 第一个数2外,是11、7、16、12、8、17、13、9、18、14、10、6、15这13个数为一个循环,即从第二名开始循环,每一个循环占13名 同学,所以 ÷13看余数是几就是对应的一个循环中的第几个数.
12.【答案】5
【解析】【解答】解:0.8571是按照285714六位进行循环的; 2001÷6=333…3; 余数是3,第2001位就和第3位相同是5. 故答案为:5. 【分析】0.8571是按照285714六位进行循环的,求出2001里面有多少个这样的循环节,还余几个数字,再根据余数判断即可.
13.【答案】31
【解析】【解答】31种, 可称1克~31克中的任何一个重量, 此题为组合题, 5个砝码选1个有5种, 5选2有10种, 5选3有10种, 5选4有4种, 5选5有1种, 合计31种。 故答案为: 31。 【分析】这是组合题目,分别找出选1到5个砝码各有几种组合,然后相加即可。
14.【答案】
【解析】【解答】解:++++++++, =+-+-+···+-, =1﹣, =. □=1﹣, =. 【分析】因为++++++++□=1,所以□=1﹣(+-+-+···+-),括号内的分数可以简算.
15.【答案】9025
【解析】【解答】解:95×95=9025 故答案为:9025 【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
16.【答案】4225
【解析】【解答】解:65×65=4225 故答案为:4225
【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
三、计算题
17.【答案】解:=2÷7=0.285714275714… 2013÷6=335…3, 循环节中第三个数是5, (2+7+5+7+1+4)×335+2+7+5 =26×335+14 =8710+14 =8724 答:小数点后面第2013位上的数字是5; 这2013个数字的和是8724.
【解析】【分析】2÷7是一个循环小数,循环节是285714,看2013由多少个循环节零几个数即可判断. 一组的和是2+7+5+7+1+4=26,共几组,就用几乘26,最后再加2加7加5即可.
18.【答案】解:=0.9230, 循环节是692307有6个数字, 2005÷6=334(个)…1, 所以第2005位上是第335个循环节的第1位数字,是6. 答:小数点后面第2005位上的数字是6.
【解析】【分析】因为=0.9230该结果是循环小数,它的循环节是692307,是6位数,2005÷6=334(个)…1,所以小数部分的第2005位数字是334个循环节后的335个循环节上的第1个数字,循环节692307的第1个数字是6,据此解答.
四、解答题
19.【答案】每次少2个。
【解析】【解答】由图数得从左到右依次是6、4、2个西瓜,因为6-4=2,4-2=2,所以每次少2个西瓜。 【分析】考查十以内的减法计算以及读图做题的能力。
20.【答案】÷7= -7??? ÷8= -8
【解析】【分析】先观察四个算式的特征,然后判断规律,被除数是分数,除数是整数,分母比除数小1,分子是除数与除数的乘积,得数是这个分数减去这个整数,按照这样的规律写出两个算式即可。
五、综合题
21.【答案】(1)14;17 (2);
【解析】【解答】(1)2+3=5,5+3=8,8+3=11,11+3=14,14+3=17 (2)=, =, =, =, =, = 故答案为:14;17; ? ;
【分析】(1)根据观察可知,前一项+3=后一项,代入计算即可得出答案。 (2)分母:n2 , 分子:n2-1(n从2开始到7),将对应数字代入即可求出结果。
六、应用题
22.【答案】解:通过数数的方法,在括号中填上相应小象的个数,分别是1、4、7,将中间一组的小象排除一个,数一数剩下的个数,就为增加的个数,由图知,增加了3个;以 相同的方法,将第三组小象排除4个,数剩下的个数,为3个,也是增加了3个。所以每次增加了3个小象。也可通过1+3=4,4+3=7,计算出每次增加3 个。
【解析】【分析】考查读图能力和十以内的加法计算。
