17.2勾股定理的逆定理(2)课件
图片预览


文档简介
人教版数学八年级下册
17.2勾股定理的逆定理(2)
2.什么是互逆命题、互逆定理?
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
1.勾股定理的逆定理的内容是什么?
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,这两个定理称为互逆定理。
3.如何判断一个三角形是否是直角三角形?
(1)有一个直角(垂直);
(2)勾股定理的逆定理.
25
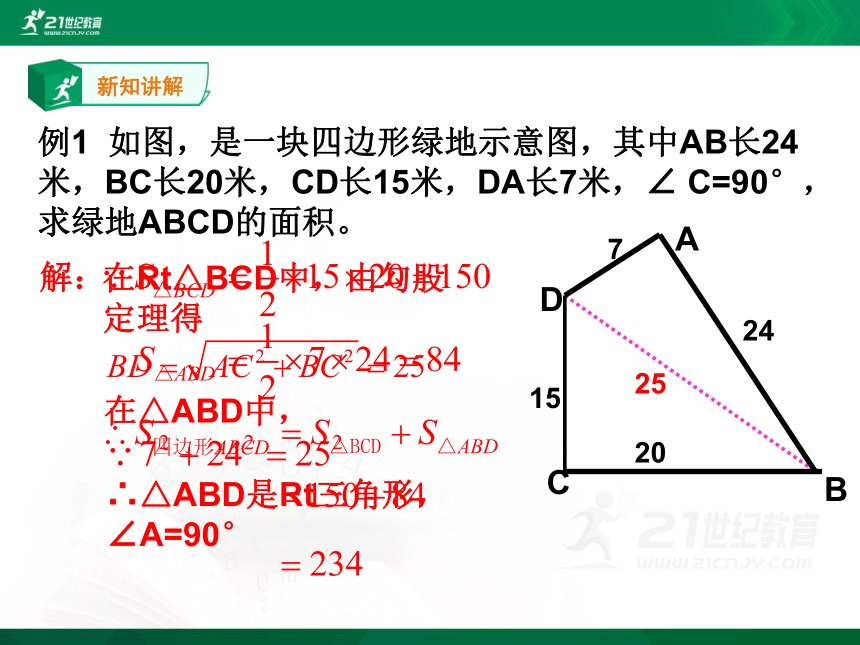
例1 如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90°,
求绿地ABCD的面积。
解:
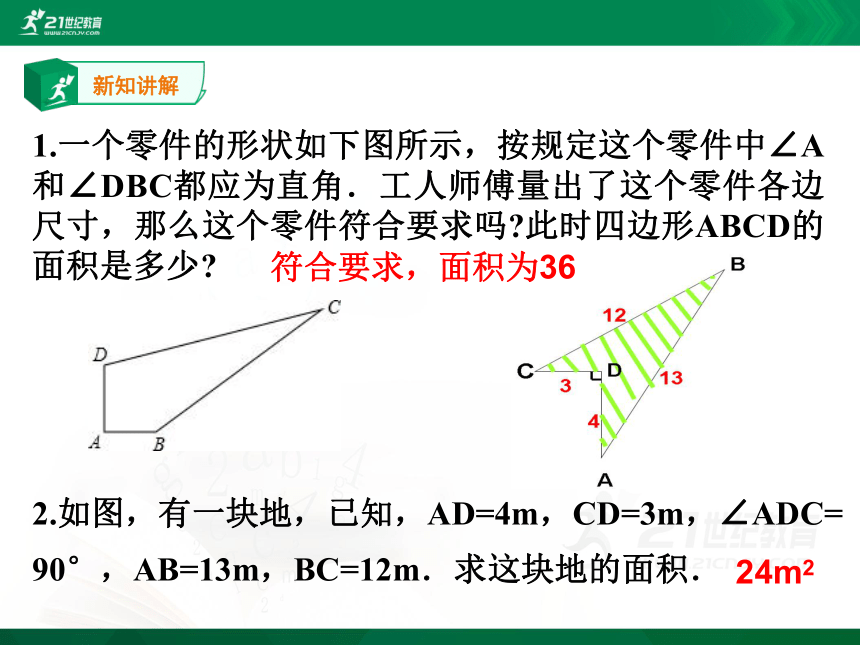
1.一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?此时四边形ABCD的面积是多少?
符合要求,面积为36
2.如图,有一块地,已知,AD=4m,CD=3m,∠ADC=
90°,AB=13m,BC=12m.求这块地的面积.
24m2
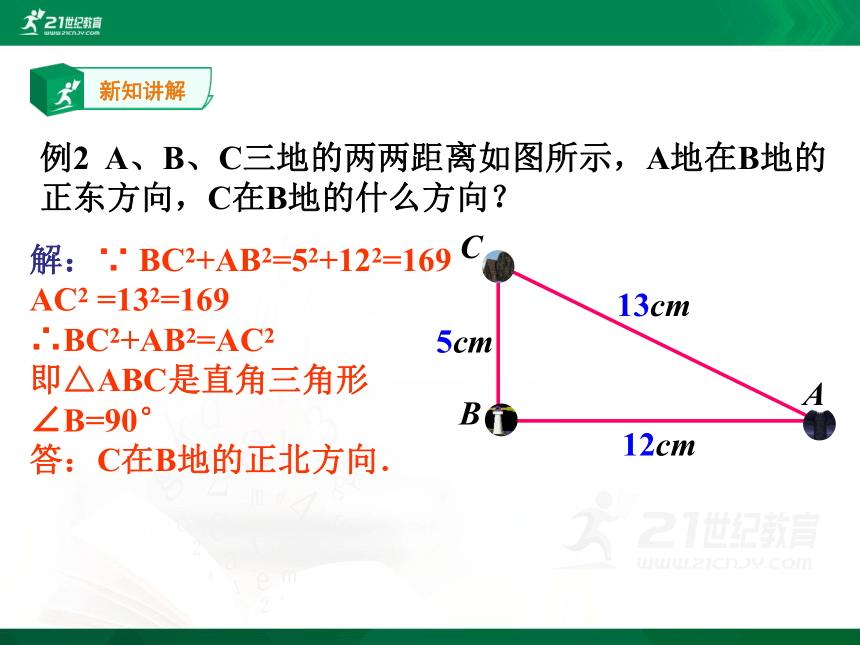
例2 A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?
解:∵ BC2+AB2=52+122=169
AC2 =132=169
∴BC2+AB2=AC2
即△ABC是直角三角形
∠B=90°
答:C在B地的正北方向.
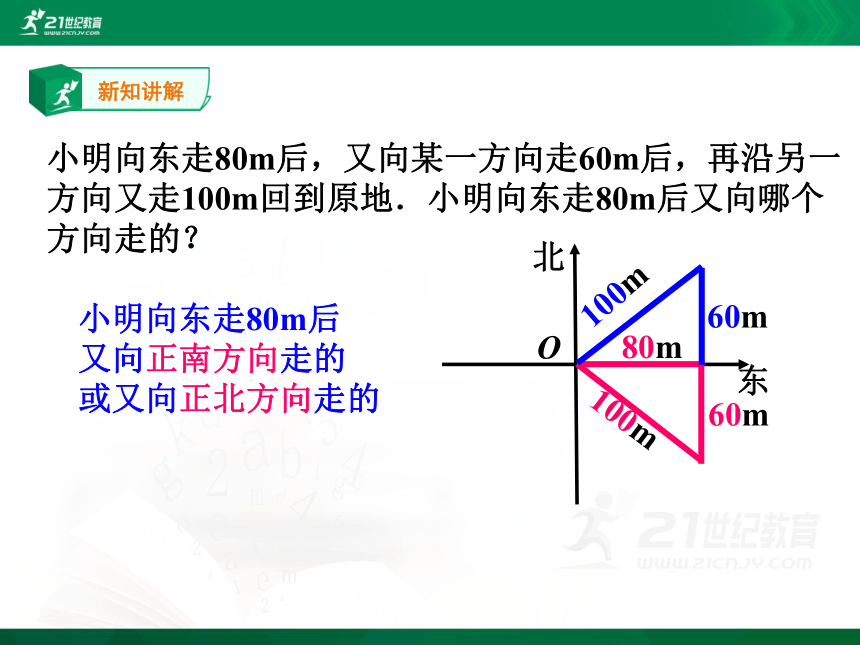
小明向东走80m后,又向某一方向走60m后,再沿另一方向又走100m回到原地.小明向东走80m后又向哪个方向走的?
80m
60m
100m
60m
100m
小明向东走80m后
又向正南方向走的
或又向正北方向走的
港口
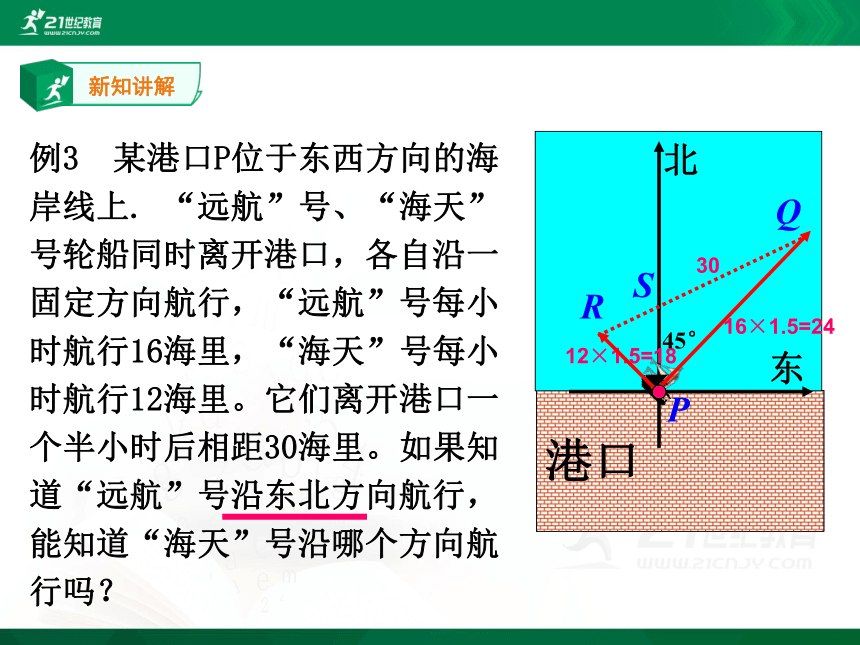
例3 某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
16×1.5=24
12×1.5=18
30
45°
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=90°
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
45°
45°
即“海天”号沿西北方向航行.
在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处,求:
(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
1000
A
B
60°
45°
C
500
例4 国家规定:小汽车在城市街道上行驶的速度不得超过70千米/时。一辆小汽车在一条城市街路的直道上行驶,某一时刻刚好行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时测得小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向?这辆小汽车超速了吗?
车速检测仪
小汽车
30米
50米
2秒后
30°
40米
60°
小汽车在车速检测仪的北偏西60°方向
25米/秒=90千米/时
>70千米/时∴小汽车超速了
你觉的此题解对了吗?
60°
45°
75°
B
15°
30°
30°
C
30
30
30°
60
乙船
甲船
甲船
如图,在我国沿海有一艘不明国际的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°.那么甲巡逻艇的航向是怎样的?
北偏东50°
通过本节课的学习,我们更加明确了勾股定理及其逆定理的用途及用法,你能说说吗?
1.必做题:教材习题17.2第4题.
2.选做题:
已知:如下图,梯形ABCD中,AD∥BC,AD=1,AB=BC=4,CD=5.求梯形ABCD的面积. Zx``````x``k
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.2勾股定理的逆定理(2)
2.什么是互逆命题、互逆定理?
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
1.勾股定理的逆定理的内容是什么?
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形,且边C所对的角为直角。
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,这两个定理称为互逆定理。
3.如何判断一个三角形是否是直角三角形?
(1)有一个直角(垂直);
(2)勾股定理的逆定理.
25
例1 如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90°,
求绿地ABCD的面积。
解:
1.一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?此时四边形ABCD的面积是多少?
符合要求,面积为36
2.如图,有一块地,已知,AD=4m,CD=3m,∠ADC=
90°,AB=13m,BC=12m.求这块地的面积.
24m2
例2 A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?
解:∵ BC2+AB2=52+122=169
AC2 =132=169
∴BC2+AB2=AC2
即△ABC是直角三角形
∠B=90°
答:C在B地的正北方向.
小明向东走80m后,又向某一方向走60m后,再沿另一方向又走100m回到原地.小明向东走80m后又向哪个方向走的?
80m
60m
100m
60m
100m
小明向东走80m后
又向正南方向走的
或又向正北方向走的
港口
例3 某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
16×1.5=24
12×1.5=18
30
45°
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=90°
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
45°
45°
即“海天”号沿西北方向航行.
在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处,求:
(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
1000
A
B
60°
45°
C
500
例4 国家规定:小汽车在城市街道上行驶的速度不得超过70千米/时。一辆小汽车在一条城市街路的直道上行驶,某一时刻刚好行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时测得小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向?这辆小汽车超速了吗?
车速检测仪
小汽车
30米
50米
2秒后
30°
40米
60°
小汽车在车速检测仪的北偏西60°方向
25米/秒=90千米/时
>70千米/时∴小汽车超速了
你觉的此题解对了吗?
60°
45°
75°
B
15°
30°
30°
C
30
30
30°
60
乙船
甲船
甲船
如图,在我国沿海有一艘不明国际的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°.那么甲巡逻艇的航向是怎样的?
北偏东50°
通过本节课的学习,我们更加明确了勾股定理及其逆定理的用途及用法,你能说说吗?
1.必做题:教材习题17.2第4题.
2.选做题:
已知:如下图,梯形ABCD中,AD∥BC,AD=1,AB=BC=4,CD=5.求梯形ABCD的面积. Zx``````x``k
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
