(苏教版) 选修2-1第3章空间向量与立体几何3.1.5空间向量的数量积课件(27张)
文档属性
| 名称 | (苏教版) 选修2-1第3章空间向量与立体几何3.1.5空间向量的数量积课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-14 12:43:55 | ||
图片预览







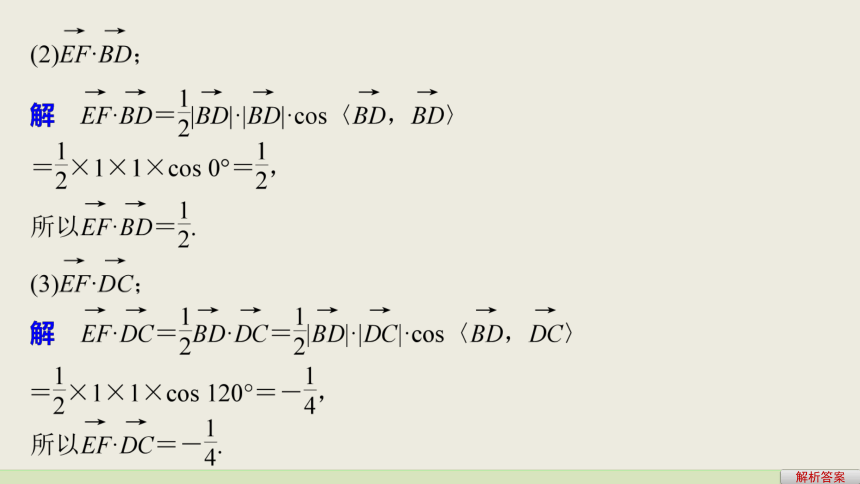
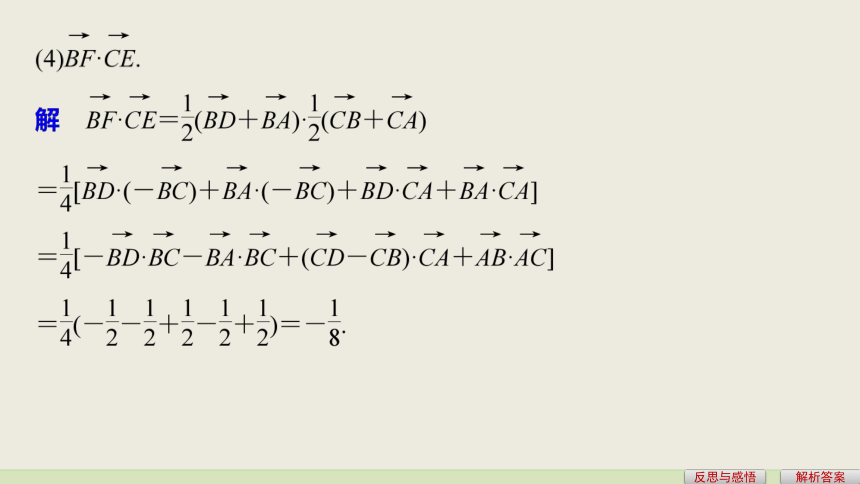
文档简介
课件27张PPT。3.1.5 空间向量的数量积1.掌握空间向量夹角的概念及表示方法,掌握两个向量的数量积的概念、性质和计算方法及运算规律.
2.掌握两个向量的数量积的主要用途,会用它解决立体几何中一些简单的问题.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 空间向量的夹角答案〈a,b〉[0,π]⊥(2)数量积的运算律知识点二 空间向量的数量积(1)定义
已知两个非零向量a,b,________________叫做a,b的数量积,记作___则|a||b|cos〈a,b〉答案a·b.(3)数量积的性质返回例1 如图所示,已知空间四边形ABCD的
每条边和对角线长都等于1,点E,F分别是
AB,AD的中点,计算: 题型探究 重点突破题型一 空间向量的数量积运算解析答案解析答案解析答案反思与感悟由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.跟踪训练1 已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为________.解析答案解析 ∵a+b+c=0,∴(a+b+c)2=0,
∴a2+b2+c2+2(a·b+b·c+c·a)=0,-13例2 如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,题型二 利用数量积求夹角解析答案反思与感悟求OA与BC所成角的余弦值.反思与感悟利用向量的数量积,求异面直线所成的角的方法:(1)根据题设条件在所求的异面直线上取两个向量;(2)将求异面直线所成角的问题转化为求向量夹角问题;(3)利用向量的数量积求角的大小;(4)证明两向量垂直可转化为数量积为零.跟踪训练2 如图所示,正四面体ABCD
的每条棱长都等于a,点M,N分别是
AB,CD的中点,
求证:MN⊥AB,MN⊥CD.解析答案例3 正三棱柱ABCA1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.题型三 利用数量积求距离解析答案反思与感悟解析答案由题意知|a|=|b|=|c|=2,
且〈a,b〉=60°,〈a,c〉=〈b,c〉=90°.反思与感悟=1+1+4-1=5,反思与感悟利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量两两之间的夹角以及它们的模,利用公式|a|= 求解即可.跟踪训练3 如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.解析答案返回返回 当堂检测123451.若a,b均为非零向量,则a·b=|a||b|是a与b共线的____________条件.解析答案解析 a·b=|a||b|cos〈a,b〉=|a||b|?cos〈a,b〉=1?〈a,b〉=0,当a与b反向时,不能成立.充分不必要123452.已知a,b均为单位向量,它们的夹角为60°,那么|a-3b|=________.解析 ∵|a-3b|2=(a-3b)2=a2-6a·b+9b2解析答案123453.对于向量a、b、c和实数λ,下列命题中的真命题是________.(填序号)
①若a·b=0,则a=0或b=0;
②若λa=0,则λ=0或a=0;
③若a2=b2,则a=b或a=-b;
④若a·b=a·c,则b=c.解析 对于①,可举反例:当a⊥b时,a·b=0;
对于③,a2=b2,只能推得|a|=|b|,而不能推出a=±b;
对于④,a·b=a·c可以移项整理得a·(b-c)=0.②解析答案12345解析答案解析 |a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,
将上面两式左、右两边分别相减,得4a·b=4,
∴a·b=1.112345解析答案5.若向量a,b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=________.将①×2-②得,2a2-b2=0,
∴b2=|b|2=2a2=2|a|2=2,课堂小结求空间向量的数量积要找到两个向量的模和夹角;利用数量积求两异面直线所成的角,关键在于在异面直线上构造向量,找出两向量的关系;证明两向量垂直可转化为证明两个向量的数量积为零,求线段长度转化为求向量的模.返回
2.掌握两个向量的数量积的主要用途,会用它解决立体几何中一些简单的问题.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 空间向量的夹角答案〈a,b〉[0,π]⊥(2)数量积的运算律知识点二 空间向量的数量积(1)定义
已知两个非零向量a,b,________________叫做a,b的数量积,记作___则|a||b|cos〈a,b〉答案a·b.(3)数量积的性质返回例1 如图所示,已知空间四边形ABCD的
每条边和对角线长都等于1,点E,F分别是
AB,AD的中点,计算: 题型探究 重点突破题型一 空间向量的数量积运算解析答案解析答案解析答案反思与感悟由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.跟踪训练1 已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为________.解析答案解析 ∵a+b+c=0,∴(a+b+c)2=0,
∴a2+b2+c2+2(a·b+b·c+c·a)=0,-13例2 如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,题型二 利用数量积求夹角解析答案反思与感悟求OA与BC所成角的余弦值.反思与感悟利用向量的数量积,求异面直线所成的角的方法:(1)根据题设条件在所求的异面直线上取两个向量;(2)将求异面直线所成角的问题转化为求向量夹角问题;(3)利用向量的数量积求角的大小;(4)证明两向量垂直可转化为数量积为零.跟踪训练2 如图所示,正四面体ABCD
的每条棱长都等于a,点M,N分别是
AB,CD的中点,
求证:MN⊥AB,MN⊥CD.解析答案例3 正三棱柱ABCA1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.题型三 利用数量积求距离解析答案反思与感悟解析答案由题意知|a|=|b|=|c|=2,
且〈a,b〉=60°,〈a,c〉=〈b,c〉=90°.反思与感悟=1+1+4-1=5,反思与感悟利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量两两之间的夹角以及它们的模,利用公式|a|= 求解即可.跟踪训练3 如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.解析答案返回返回 当堂检测123451.若a,b均为非零向量,则a·b=|a||b|是a与b共线的____________条件.解析答案解析 a·b=|a||b|cos〈a,b〉=|a||b|?cos〈a,b〉=1?〈a,b〉=0,当a与b反向时,不能成立.充分不必要123452.已知a,b均为单位向量,它们的夹角为60°,那么|a-3b|=________.解析 ∵|a-3b|2=(a-3b)2=a2-6a·b+9b2解析答案123453.对于向量a、b、c和实数λ,下列命题中的真命题是________.(填序号)
①若a·b=0,则a=0或b=0;
②若λa=0,则λ=0或a=0;
③若a2=b2,则a=b或a=-b;
④若a·b=a·c,则b=c.解析 对于①,可举反例:当a⊥b时,a·b=0;
对于③,a2=b2,只能推得|a|=|b|,而不能推出a=±b;
对于④,a·b=a·c可以移项整理得a·(b-c)=0.②解析答案12345解析答案解析 |a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,
将上面两式左、右两边分别相减,得4a·b=4,
∴a·b=1.112345解析答案5.若向量a,b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=________.将①×2-②得,2a2-b2=0,
∴b2=|b|2=2a2=2|a|2=2,课堂小结求空间向量的数量积要找到两个向量的模和夹角;利用数量积求两异面直线所成的角,关键在于在异面直线上构造向量,找出两向量的关系;证明两向量垂直可转化为证明两个向量的数量积为零,求线段长度转化为求向量的模.返回
