八年级下册数学18.1平行四边形助学案(5课时 无答案)
文档属性
| 名称 | 八年级下册数学18.1平行四边形助学案(5课时 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-14 20:05:01 | ||
图片预览




文档简介
课题 平行四边形的性质(1) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1.理解并掌握平行四边形的概念和平行四边形的性质. 2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
重点 平行四边形的定义,平行四边形的性质及其应用.
难点 运用平行四边形的性质进行有关的论证和计算.
学习过程 学(教)记录
【自助学习·我尝试自学】 (自学课本41页至42页并回答问题) 1、定义:有两组对边__________________的四边形叫平形四边形, 请你用数学几何语言给平行四边形下个定义: ∵ ∥ , ∥ ∴四边形ABCD是平行四边形 2、表示:平行四边形用“____”表示,平行四边形ABCD记作_______。 注意:表示一般按一定的方向依次写出各顶点字母 3、对角线的定义:平行四边形 两个顶点连成的 叫做它的对角线。 4、如图□ABCD中,对边有___组,分别是_________,对角有___组,分别是_____________,对角线有______条,它们是________。 【互助探究·我参与互研】 观察:请你剪两个一样的口ABCD,作出两条对角线交于点O,将其中一个旋转180°,然后重合在一起,仔细观察完成下列各题: (1)∠A与∠ 重合,∠B与∠ 重合,因此:∠A=∠ ,∠B=∠ 。 猜想: 平行四边形的 相等 (2)AB与 重合,BC与 重合,因此:AB= ,BC= 。 猜想:平行四边形的 相等 验证:已知:如图ABCD,求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD. 归纳出平行四边形的性质: 文字叙述几何表示边两组对边平行AB∥CD AD∥BC角
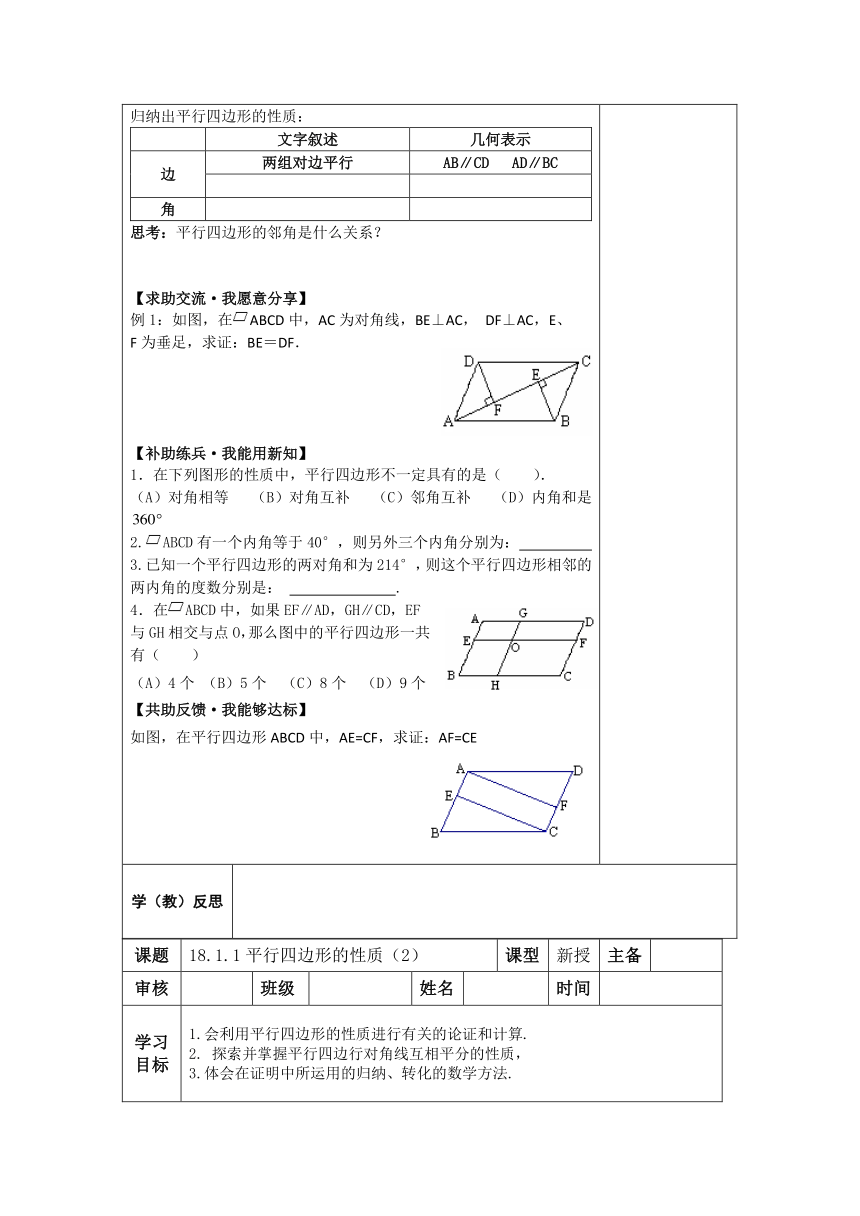
思考:平行四边形的邻角是什么关系? 【求助交流·我愿意分享】 例1:如图,在ABCD中,AC为对角线,BE⊥AC, DF⊥AC,E、F为垂足,求证:BE=DF. 【补助练兵·我能用新知】 1.在下列图形的性质中,平行四边形不一定具有的是( ). (A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是 2.ABCD有一个内角等于40°,则另外三个内角分别为: 3.已知一个平行四边形的两对角和为214°,则这个平行四边形相邻的两内角的度数分别是: . 4.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( ) (A)4个 (B)5个 (C)8个 (D)9个 【共助反馈·我能够达标】 如图,在平行四边形ABCD中,AE=CF,求证:AF=CE
学(教)反思
课题 18.1.1平行四边形的性质(2) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1.会利用平行四边形的性质进行有关的论证和计算. 2. 探索并掌握平行四边行对角线互相平分的性质, 3.体会在证明中所运用的归纳、转化的数学方法.
重点 使学生掌握平行四边行对角线互相平分的性质.
难点 平行四边行性质的综合应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 1、什么样的四边形是平行四边形?四边形与平行四边形的关系是: 2、平行四边形的性质: 【互助探究·我参与互研】 请学生在纸上画两个全等的ABCD和EFGH,并连接对角线AC、BD和EG、HF,设它们分别交于点O.把这两个平行四边形落在一起,在点O处钉一个图钉,将ABCD绕点O旋转,观察它还和EFGH重合吗?你能从子中看出前面所得到的平行四边形的边、角关系吗?进一步,你还能发现平行四边形的什么性质吗? 由上面的探究你能得到什么【结论】: 2、用以前学过的知识证明性质定理3: 3、性质定理3的数学语言: 【求助交流·我愿意分享】 已知:如图ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F. 求证:OE=OF,AE=CF,BE=DF. 【补助练兵·我能用新知】 1.在平行四边形中,周长等于48, 已知一边长12,求各边的长: ; 已知AB=2BC,求各边的长: ; 已知对角线AC、BD交于点O,△AOD与△AOB的周长的差是10,求各边的长: 。 2.如图,ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,求△OBC的周长。 【共助反馈·我能够达标】 已知:ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F. 求证:OE=OF,AE=CF,BE=DF.
学(教)反思
课题 18.1.2平行四边形判定(1) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握用“对角线互相平分的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算; 2、理解“两组对角(对边)分别相等的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算;
重点 平行四边形的判定方法及应用.
难点 平行四边形的判定定理与性质定理的灵活应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 1.用定义法证明一个四边形是平行四边形时,要什么条件? 2.用所学的判定方法判定一个四边形是平行四边形的条件是什么? 3.平行四边形的对角线互相平分的逆命题如何表达?是否是真命题? 【互助探究·我参与互研】 小明的父亲手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗? 让学生利用手中的学具——硬纸板条通过观察、测量、猜想、验证、探索构成平行四边形的条件,思考并探讨: (1)你能适当选择手中的硬纸板条搭建一个平行四边形吗? (2)你怎样验证你搭建的四边形一定是平行四边形? (3)你能说出你的做法及其道理吗? (4)能否将你的探索结论作为平行四边形的一种判别方法?你能用文字语言表述出来吗? (5)你还能找出其他方法吗? 从探究中得到:平行四边形判定方法1 平行四边形判定方法2 【求助交流·我愿意分享】 1.如图,在四边形ABCD中,AC、BD相交于点O, (1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形; (2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形. 2.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O. 求证:EO=OF. 【补助练兵·我能用新知】 1.下列条件中能判断四边形是平行四边形的是( ). (A)对角线互相垂直 (B)对角线相等 (C)对角线互相垂直且相等 (D)对角线互相平分 2.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC,求证:BE=CF 【共助反馈·我能够达标】 小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由.
学(教)反思
课题 18.1.2平行四边形判定(2) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握用一组对边平行且相等来判定平行四边形的方法 2、熟练掌握平行四边形判定的五种方法,并通过定理、习题的证明提高逻辑思维能力; 3、进一步掌握平行四边形性质与判定之间的区别与联系
重点 平行四边形各种判定方法及应用,尤其是根据不同条件能正确地选择判定方法.
难点 平行四边形的判定定理与性质定理的综合应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 我们已学过的平行四边形的判定方法有哪些? 1、从边看:(1) 是平行四边形 (2) 是平行四边形 2、从对角线看: 是平行四边形 3、从角看: 是平行四边形 【互助探究·我参与互研】 想一想1、如图,四边形ABCD中,AB∥CD,AB=CD。四边形ABCD是平行四边形吗? 2、归纳: 的四边形是平行四边形 3、小结:平行四边形判定的五种方法 【新知运用】 如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF. 【求助交流·我愿意分享】 1.(选择)在下列给出的条件中,能判定四边形ABCD为平行四边形的是( ). (A)AB∥CD,AD=BC (B)∠A=∠B,∠C=∠D (C)AB=CD,AD=BC (D)AB=AD,CB=CD 2.已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由. 【补助练兵·我能用新知】 1.判断题: (1)相邻的两个角都互补的四边形是平行四边形( ); (2)两组对角分别相等的四边形是平行四边形( ); (3)一组对边平行,另一组对边相等的四边形是平行四边形( ); (4)一组对边平行且相等的四边形是平行四边形( ); (5)对角线相等的四边形是平行四边形( ); (6)对角线互相平分的四边形是平行四边形( ). 2.已知:ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形。 【共助反馈·我能够达标】 如图,中,、分别在、上,与交于点,与交于点,猜想与间的关系,并证明你的猜想。
学(教)反思
课题 18.1.2平行四边形判定-三角形的中位线 课型 新授 主备
审核 班级 姓名 时间
学习 目标 理解三角形中位线的概念,掌握它的性质. 能较熟练地应用三角形中位线性质进行有关的证明和计算. 3.能运用综合法证明有关三角形中位线性质的结论.理解在证明过程中所运用的归纳、类比、转化等思想方法.
重点 掌握和运用三角形中位线的性质.
难点 三角形中位线性质的证明(辅助线的添加方法)
学习过程 学(教)记录
【自助学习·我尝试自学】 平行四边形的性质和平行四边形的判定之间有什么联系? 你能说说平行四边形性质与判定的用途吗? 【互助探究·我参与互研】 (1)、将任意一个三角形分成四个全等的三角形,你是如何切割的? (2)、图中有几个平行四边形?你是如何判断的? (3)、 叫做三角形的中位线. (4)、想一想:①、一个三角形的中位线共有几条?②、三角形的中位线与中线有什么区别? (5)、三角形的中位线与第三边有怎样的关系? 【新知运用】 如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=BC. 结论:三角形中位线的性质 【求助交流·我愿意分享】 1.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20 m,那么A、B两点的距离是 m,理由是 . 2.已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长. 3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点,(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm; (2)中线AF与DE中位线有什么特殊的关系?证明你的猜想. 【补助练兵·我能用新知】 1.一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是 cm. 2.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm. 3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 【共助反馈·我能够达标】 如图,E、F、G、H分别是四边形ABCD的中点.求证:四边形EFGH是平行四边形.
学(教)反思
审核 班级 姓名 时间
学习 目标 1.理解并掌握平行四边形的概念和平行四边形的性质. 2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
重点 平行四边形的定义,平行四边形的性质及其应用.
难点 运用平行四边形的性质进行有关的论证和计算.
学习过程 学(教)记录
【自助学习·我尝试自学】 (自学课本41页至42页并回答问题) 1、定义:有两组对边__________________的四边形叫平形四边形, 请你用数学几何语言给平行四边形下个定义: ∵ ∥ , ∥ ∴四边形ABCD是平行四边形 2、表示:平行四边形用“____”表示,平行四边形ABCD记作_______。 注意:表示一般按一定的方向依次写出各顶点字母 3、对角线的定义:平行四边形 两个顶点连成的 叫做它的对角线。 4、如图□ABCD中,对边有___组,分别是_________,对角有___组,分别是_____________,对角线有______条,它们是________。 【互助探究·我参与互研】 观察:请你剪两个一样的口ABCD,作出两条对角线交于点O,将其中一个旋转180°,然后重合在一起,仔细观察完成下列各题: (1)∠A与∠ 重合,∠B与∠ 重合,因此:∠A=∠ ,∠B=∠ 。 猜想: 平行四边形的 相等 (2)AB与 重合,BC与 重合,因此:AB= ,BC= 。 猜想:平行四边形的 相等 验证:已知:如图ABCD,求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD. 归纳出平行四边形的性质: 文字叙述几何表示边两组对边平行AB∥CD AD∥BC角
思考:平行四边形的邻角是什么关系? 【求助交流·我愿意分享】 例1:如图,在ABCD中,AC为对角线,BE⊥AC, DF⊥AC,E、F为垂足,求证:BE=DF. 【补助练兵·我能用新知】 1.在下列图形的性质中,平行四边形不一定具有的是( ). (A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是 2.ABCD有一个内角等于40°,则另外三个内角分别为: 3.已知一个平行四边形的两对角和为214°,则这个平行四边形相邻的两内角的度数分别是: . 4.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( ) (A)4个 (B)5个 (C)8个 (D)9个 【共助反馈·我能够达标】 如图,在平行四边形ABCD中,AE=CF,求证:AF=CE
学(教)反思
课题 18.1.1平行四边形的性质(2) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1.会利用平行四边形的性质进行有关的论证和计算. 2. 探索并掌握平行四边行对角线互相平分的性质, 3.体会在证明中所运用的归纳、转化的数学方法.
重点 使学生掌握平行四边行对角线互相平分的性质.
难点 平行四边行性质的综合应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 1、什么样的四边形是平行四边形?四边形与平行四边形的关系是: 2、平行四边形的性质: 【互助探究·我参与互研】 请学生在纸上画两个全等的ABCD和EFGH,并连接对角线AC、BD和EG、HF,设它们分别交于点O.把这两个平行四边形落在一起,在点O处钉一个图钉,将ABCD绕点O旋转,观察它还和EFGH重合吗?你能从子中看出前面所得到的平行四边形的边、角关系吗?进一步,你还能发现平行四边形的什么性质吗? 由上面的探究你能得到什么【结论】: 2、用以前学过的知识证明性质定理3: 3、性质定理3的数学语言: 【求助交流·我愿意分享】 已知:如图ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F. 求证:OE=OF,AE=CF,BE=DF. 【补助练兵·我能用新知】 1.在平行四边形中,周长等于48, 已知一边长12,求各边的长: ; 已知AB=2BC,求各边的长: ; 已知对角线AC、BD交于点O,△AOD与△AOB的周长的差是10,求各边的长: 。 2.如图,ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,求△OBC的周长。 【共助反馈·我能够达标】 已知:ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F. 求证:OE=OF,AE=CF,BE=DF.
学(教)反思
课题 18.1.2平行四边形判定(1) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握用“对角线互相平分的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算; 2、理解“两组对角(对边)分别相等的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算;
重点 平行四边形的判定方法及应用.
难点 平行四边形的判定定理与性质定理的灵活应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 1.用定义法证明一个四边形是平行四边形时,要什么条件? 2.用所学的判定方法判定一个四边形是平行四边形的条件是什么? 3.平行四边形的对角线互相平分的逆命题如何表达?是否是真命题? 【互助探究·我参与互研】 小明的父亲手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗? 让学生利用手中的学具——硬纸板条通过观察、测量、猜想、验证、探索构成平行四边形的条件,思考并探讨: (1)你能适当选择手中的硬纸板条搭建一个平行四边形吗? (2)你怎样验证你搭建的四边形一定是平行四边形? (3)你能说出你的做法及其道理吗? (4)能否将你的探索结论作为平行四边形的一种判别方法?你能用文字语言表述出来吗? (5)你还能找出其他方法吗? 从探究中得到:平行四边形判定方法1 平行四边形判定方法2 【求助交流·我愿意分享】 1.如图,在四边形ABCD中,AC、BD相交于点O, (1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形; (2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形. 2.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O. 求证:EO=OF. 【补助练兵·我能用新知】 1.下列条件中能判断四边形是平行四边形的是( ). (A)对角线互相垂直 (B)对角线相等 (C)对角线互相垂直且相等 (D)对角线互相平分 2.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC,求证:BE=CF 【共助反馈·我能够达标】 小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由.
学(教)反思
课题 18.1.2平行四边形判定(2) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握用一组对边平行且相等来判定平行四边形的方法 2、熟练掌握平行四边形判定的五种方法,并通过定理、习题的证明提高逻辑思维能力; 3、进一步掌握平行四边形性质与判定之间的区别与联系
重点 平行四边形各种判定方法及应用,尤其是根据不同条件能正确地选择判定方法.
难点 平行四边形的判定定理与性质定理的综合应用.
学习过程 学(教)记录
【自助学习·我尝试自学】 我们已学过的平行四边形的判定方法有哪些? 1、从边看:(1) 是平行四边形 (2) 是平行四边形 2、从对角线看: 是平行四边形 3、从角看: 是平行四边形 【互助探究·我参与互研】 想一想1、如图,四边形ABCD中,AB∥CD,AB=CD。四边形ABCD是平行四边形吗? 2、归纳: 的四边形是平行四边形 3、小结:平行四边形判定的五种方法 【新知运用】 如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF. 【求助交流·我愿意分享】 1.(选择)在下列给出的条件中,能判定四边形ABCD为平行四边形的是( ). (A)AB∥CD,AD=BC (B)∠A=∠B,∠C=∠D (C)AB=CD,AD=BC (D)AB=AD,CB=CD 2.已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由. 【补助练兵·我能用新知】 1.判断题: (1)相邻的两个角都互补的四边形是平行四边形( ); (2)两组对角分别相等的四边形是平行四边形( ); (3)一组对边平行,另一组对边相等的四边形是平行四边形( ); (4)一组对边平行且相等的四边形是平行四边形( ); (5)对角线相等的四边形是平行四边形( ); (6)对角线互相平分的四边形是平行四边形( ). 2.已知:ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形。 【共助反馈·我能够达标】 如图,中,、分别在、上,与交于点,与交于点,猜想与间的关系,并证明你的猜想。
学(教)反思
课题 18.1.2平行四边形判定-三角形的中位线 课型 新授 主备
审核 班级 姓名 时间
学习 目标 理解三角形中位线的概念,掌握它的性质. 能较熟练地应用三角形中位线性质进行有关的证明和计算. 3.能运用综合法证明有关三角形中位线性质的结论.理解在证明过程中所运用的归纳、类比、转化等思想方法.
重点 掌握和运用三角形中位线的性质.
难点 三角形中位线性质的证明(辅助线的添加方法)
学习过程 学(教)记录
【自助学习·我尝试自学】 平行四边形的性质和平行四边形的判定之间有什么联系? 你能说说平行四边形性质与判定的用途吗? 【互助探究·我参与互研】 (1)、将任意一个三角形分成四个全等的三角形,你是如何切割的? (2)、图中有几个平行四边形?你是如何判断的? (3)、 叫做三角形的中位线. (4)、想一想:①、一个三角形的中位线共有几条?②、三角形的中位线与中线有什么区别? (5)、三角形的中位线与第三边有怎样的关系? 【新知运用】 如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=BC. 结论:三角形中位线的性质 【求助交流·我愿意分享】 1.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20 m,那么A、B两点的距离是 m,理由是 . 2.已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长. 3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点,(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm; (2)中线AF与DE中位线有什么特殊的关系?证明你的猜想. 【补助练兵·我能用新知】 1.一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是 cm. 2.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm. 3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 【共助反馈·我能够达标】 如图,E、F、G、H分别是四边形ABCD的中点.求证:四边形EFGH是平行四边形.
学(教)反思
