六年级下册数学一课一练-2.圆柱和圆锥 青岛版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-2.圆柱和圆锥 青岛版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 55.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-16 00:00:00 | ||
图片预览


文档简介
六年级下册数学一课一练-2.圆柱和圆锥
一、单选题
1.一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是()立方厘米。
A.? n?????????????????????????????????????????/B.?2n?????????????????????????????????????????/C.?3n?????????????????????????????????????????/D.?4n
2.用一张长6.28分米,宽4分米的长方形苇席围成一个圆柱体的粮囤(接头部分不计).用(?? )做底面周长,围成的粮囤容积大.
A.?长????????????????????????????????????????????????B.?宽
3.把棱长是2分米的正方体木块,削成一个最大的圆柱,这个圆柱的体积是(?? )立方分米.
A.?6.28???????????????????????????????????/B.?12.56???????????????????????????????????/C.?28.26???????????????????????????????????/D.?3.14
4.高12厘米的圆锥形容器里装满了水,把这些水全部倒入与它等底等高的圆柱形量杯内,水面高( )厘米.(容器厚度忽略不计)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?12
5.一块圆柱形橡皮泥,能捏成( )个和它等底等高的圆锥形橡皮泥.
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
6.一个圆柱的高是底面直径的π倍,这个圆柱侧面的展开图是一个( )
A.?平行四边形???????????????????????????????/B.?正方形???????????????????????????????/C.?长方形???????????????????????????????/D.?圆形
7.一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是(? )立方分米.
A.?50.24????????????????????????????????????????/B.?100.48????????????????????????????????????????/C.?64
二、判断题
8.一个圆柱与一个圆锥,它们的底面积和体积都相等.那么圆锥的高是圆柱高的 /.
9.把一个圆柱体削成一个与它等底等高的圆锥体,这个圆锥体的体积是削去部分的50%。
10.如果圆锥的底面积是圆柱底面积的3倍,则圆锥和圆柱的体积相等.
11.圆锥的底面积越大,它的体积一定就越大.
12.两个圆锥的底和高各不相等,则两个圆锥的体积也一定不相等。
三、填空题
13.一根圆柱形钢材,长1米,横截面直径1厘米,这根钢材的体积是________立方厘米?如果每立方厘米钢重7.8克,这根钢材重________克?(得数保留整数)
14.体育馆里的圆柱形状的柱子,底面周长2.5米,高5.2米.如果在柱子的侧面涂上油漆,每根柱子涂油漆的面积是________平方米?
15.一个圆柱体的底面直径4分米,高0.5分米,它的侧面积是________平方分米;它的表面积是________平方分米;它的体积是________立方分米.
16.圆柱的两个底面是两个大小________的圆,如果一个圆柱的底面周长和高相等,那么它的侧面展开是一个________。
17.一个圆柱和一个圆锥等底等高,它们的体积之和是48立方分米,那么圆锥的体积是________立方分米,圆柱的体积是________立方分米。
18.把一个圆柱削成一个最大的圆锥,那么圆锥的体积是削去部分体积的________。
四、计算题
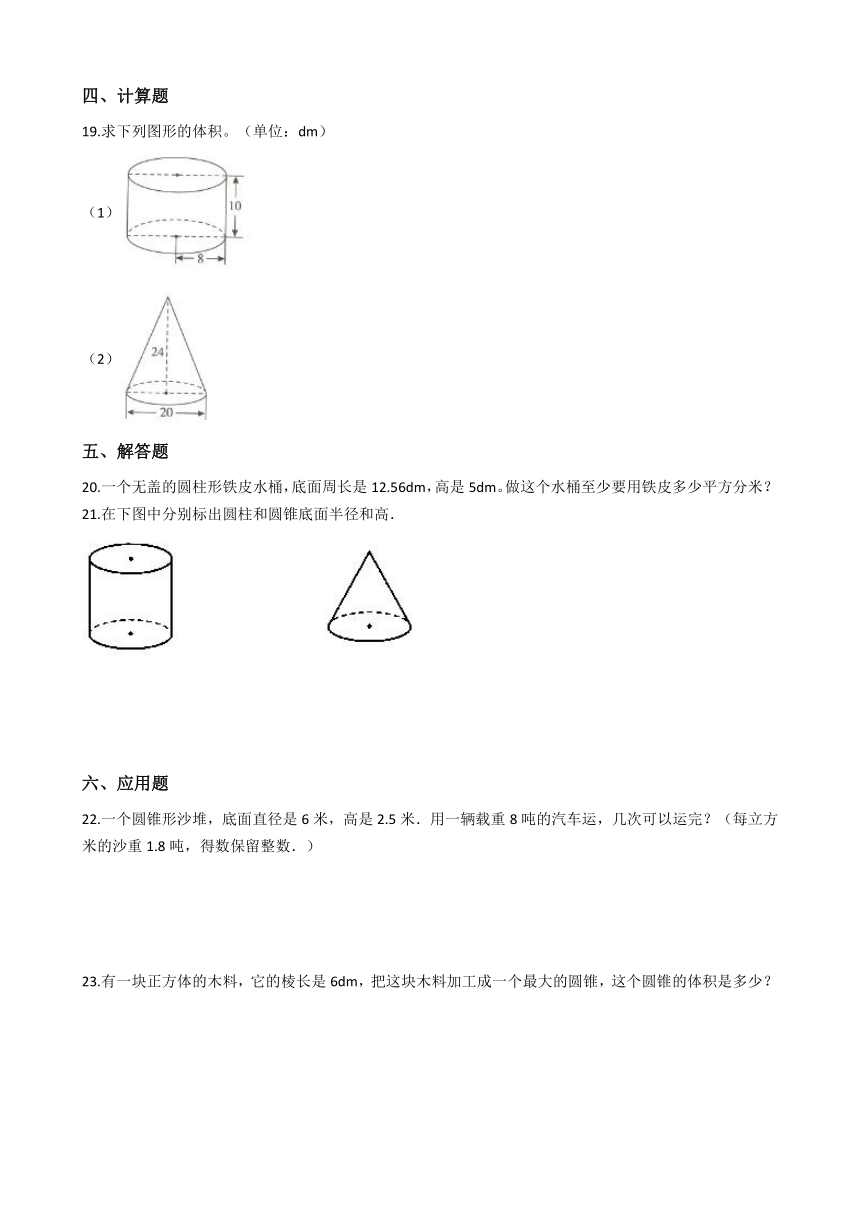
19.求下列图形的体积。(单位:dm)
(1)/
(2)/
五、解答题
20.一个无盖的圆柱形铁皮水桶,底面周长是12.56dm,高是5dm。做这个水桶至少要用铁皮多少平方分米?
21.在下图中分别标出圆柱和圆锥底面半径和高.
/
六、应用题
22.一个圆锥形沙堆,底面直径是6米,高是2.5米.用一辆载重8吨的汽车运,几次可以运完?(每立方米的沙重1.8吨,得数保留整数.)
23.有一块正方体的木料,它的棱长是6dm,把这块木料加工成一个最大的圆锥,这个圆锥的体积是多少?
答案解析部分
一、单选题
1.【答案】C
【解析】解答:由题意可知,设圆柱的体积、圆锥的体积分别是 /,由题意可知: /
分析:圆锥的体积公式和圆柱的体积公式。
2.【答案】A
【解析】【解答】圆柱的底面周长越长,这个圆柱的底面半径就越长,体积就越大。 故答案为:A。 【分析】根据题干分析可得,有两种不同的围法:一种是以6.28分米为底面周长,4分米为高,另一种是以4分米为底面周长,6.28分米为高,据此利用圆柱的容积公式求出它们的容积即可解答。
3.【答案】A
【解析】【解答】解:根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,
圆柱的体积是:
3.14×(2÷2)2×2
=3.14×1×2
=6.28(立方分米).
答:这个圆柱的体积是6.28立方分米.
故选:A.
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的体积公式计算即可.
4.【答案】B
【解析】【解答】解:倒入前后的水体积相同,等底等高的圆柱的体积是圆锥的体积的3倍,
所以把水全部倒入圆柱形量杯内,水的体积只占了圆柱形量杯的 /,所以水的高度也是占了整个量杯高度的 /;
已知量杯的高度为12厘米,所以水的高度是:12× /=4(厘米).
故选:B.
【分析】倒入前后的水体积相同,等底等高的圆柱的体积是圆锥的体积的3倍,所以把水全部倒入圆柱形量杯内,水的体积只占了圆柱形量杯的 /,所以水的高度也是占了整个量杯高度的 /,已知量杯的高度为12厘米,由此即可求得水的高度.
5.【答案】C
【解析】【解答】解:根据等底等高的圆锥形的体积是圆柱形体积的 /,
又因为,在捏橡皮泥的过程中,它的总体积不变,
所以能捏成3个和它等底等高的圆锥形橡皮泥,
故选:C.
【分析】根据题意知道,在捏橡皮泥的过程中,它的总体积不变,再根据等底等高的圆锥形和圆柱形的关系,即可得到答案.
6.【答案】B
【解析】【解答】解:因为圆柱的底面周长C=πd,圆柱的高h=πd,
则这个圆柱的底面周长和高相等,即展开后的长方形的长和宽相等,
所以说这个圆柱侧面的展开图是一个正方形;
故选:B.
【分析】根据“圆柱的侧面展开后是长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高”可知:圆柱的底面周长C=πd,由“一个圆柱的高是底面直径的π倍”可得:圆柱的高h=πd,则这个圆柱的底面周长和高相等,即展开后的长方形的长和宽相等,所以说这个圆柱侧面的展开图是一个正方形.
7.【答案】A
【解析】【解答】解:3.14×(4÷2)2×4,
=3.14×22×4,
=3.14×4×4,
=50.24(立方分米);
答:体积是50.24立方分米.
故答案为50.24.
【分析】要求圆柱体的体积,须知道圆柱的底面半径和圆柱的高,从一个棱长4分米的正方体木块削成一个最大的圆柱体,可知圆柱的高和底面直径都是4分米,由此问题得解.此题主要考查圆柱体的体积计算公式:V=πr2h,解答时一定要注意分清题目中条件,灵活解答.
二、判断题
8.【答案】错误
【解析】【解答】设圆柱和圆锥的体积都是V,底面积都是S,则 圆柱的高是:V÷S=/, 圆锥的高是:3V÷S=/, /÷/=3,原题说法错误. 故答案为:错误.
【分析】根据题意,设圆柱和圆锥的体积都是V,底面积都是S,分别表示出圆柱和圆锥的高,然后相除即可解答.
9.【答案】正确
【解析】解答:设圆柱的体积、圆锥的体积和削去部分的体积分别是 /,因为削出的圆锥与圆柱等底等高,所以 /。
分析:等底等高的圆柱的体积、圆锥的体积及削去部分的体积之间的关系。
10.【答案】错误
【解析】【解答】圆柱和圆锥的高不确定,无法确定圆柱和圆锥的体积,原题说法错误. 故答案为:错误 【分析】圆柱和圆锥的体积与底面积和高的大小有关,只确定底面积,不确定高,就无法确定体积的大小.
11.【答案】错误
【解析】【解答】圆锥的高不确定,无法确定体积的大小;原题说法错误. 故答案为:错误 【分析】圆锥的体积与底面积和高的大小有关,只确定底面积,不确定高,就无法确定体积的大小.
12.【答案】错误
【解析】【解答】解:例如:一个圆锥底面积是10高是3,体积是10;另一个圆锥底面积是5,高是6,体积也是10;原题说法错误. 故答案为:错误
【分析】圆锥的体积=底面积×高×/,圆锥的底面积和高不相等,并不能说明两个圆锥的体积不相等.
三、填空题
13.【答案】79;612
【解析】【解答】1米=100厘米 3.14×(1÷2)2×100 =3.14×0.25×100 ≈79(立方厘米) 78.5×7.8≈612(克) 【分析】首先统一单位把1米化成100厘米,然后根据圆柱的体积=底面积×高求出钢材的体积,再用钢材的体积乘每立方厘米钢重量即可。
14.【答案】13
【解析】【解答】2.5×5.2=13(平方米) 【分析】此题重点考查圆柱体的侧面积公式s=ch的掌握与运用情况,解答此题应注意分清求的是几个面的面积,据此列式计算即可。
15.【答案】6.28;31.4;6.28
【解析】【解答】解:(1)圆柱的侧面积为:3.14×4×0.5 =12.56×0.5, =6.28(平方分米);(2)圆柱的底面半径为:4÷2=2(分米), 圆柱的表面积为:3.14×22×2+6.28 =12.56×2+6.28, =25.12+6.28, =31.4(平方分米);(3)圆柱的体积为:3.14×22×0.5 =12.56×0.5, =6.28(立方分米); 答:圆柱的侧面积是6.28平方分米,表面积为31.4平方分米,圆柱的体积是6.28立方分米. 故答案为:6.28,31.4,6.28. 【分析】根据题意,可利用圆柱体的侧面积=底面周长×高,圆柱的表面积=侧面积+两个底面的面积,圆柱的体积=底面积×高进行计算即可得到答案.
16.【答案】相等;正方形
【解析】【解答】解:根据圆柱的特征可知,圆柱的两个底面是两个大小相等的圆,如果一个圆柱的底面周长和高相等,那么它的侧面展开是一个正方形. 故答案为:相等;正方形 【分析】圆柱的上下两个底面大小相等,侧面是一个曲面,侧面展开后是一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,另一条边与高相等;如果底面周长和高相等,侧面展开就是一个正方形.
17.【答案】12 ;36
【解析】【解答】解:48÷(3+1)=12(立方分米),圆锥体积是12立方分米,圆柱体积为:12×3=36(立方分米). 故答案为:12;36.
【分析】等底等高的圆柱体积是圆锥体积的3倍,再用体积和除以(3+1)求出一份是多少,再用3乘12求出圆柱体积.
18.【答案】/
【解析】【解答】解:削成的圆锥体积是1,圆柱的体积是3,圆锥的体积是削去部分体积的:1÷(3-1)=/. 故答案为:/
【分析】等底等高的圆柱体积是圆锥体积的3倍,因此削成的最大圆锥体积是1,圆柱的体积就是3,削去的部分是(3-1);用圆锥的体积除以削去部分的体积即可.
四、计算题
19.【答案】(1)πr2h=3.14×82×10=2009.6(dm3) (2)/πr2h=/×3.14× 2×24=2512(dm3)
【解析】【分析】根据圆柱的体积公式V=sh=πr2h,圆锥的体积公式V=?/sh=/πr2h,代入数据即可求解。
五、解答题
20.【答案】解:(12.56÷3.14÷2)2×3.14+12.56×5 =4×3.14+62.8 =12.56+62.8 =75.36(dm2)
答:做这个水桶至少要用铁皮75.36平方分米.
【解析】【分析】用底面周长除以3.14再除以2求出底面半径,然后用底面积加上侧面积即可求出需要铁皮的面积,圆柱的侧面积=底面周长×高.
21.【答案】/
【解析】【分析】圆柱的上下两个面叫做底面,它们是完全相同的两个圆,两个底之间的距离是圆柱的高,可以将两个圆的圆心相连即可得到高,底面圆的半径是圆柱的底面半径,连接圆锥的顶点和底面圆心的线段是圆锥的高,底面圆的半径是圆锥的底面半径,据此解答.
六、应用题
22.【答案】解: /×3.14×(6÷2)2×2.5×1.8÷8, =9.42×2.5×1.8÷8, =23.55×1.8÷8, =42.39÷8, ≈6(次), 答:6次可以运完
【解析】【分析】根据圆锥的体积公式V= /sh,求出圆锥形沙堆的体积,进而求出沙堆的重量,最后用沙堆的重量除以8吨就是要求的答案.
23.【答案】解: /
= /
=56.52(立方分米),
答:这个圆锥的体积是56.52立方分米
【解析】【分析】根据题意可知:把棱长是6分米的正方体木料加工成一个最大的圆锥,这个圆锥的底面直径和高都等于正方体的棱长,根据圆锥的体积公式:v= /,把数据代入公式解答.
一、单选题
1.一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是()立方厘米。
A.? n?????????????????????????????????????????/B.?2n?????????????????????????????????????????/C.?3n?????????????????????????????????????????/D.?4n
2.用一张长6.28分米,宽4分米的长方形苇席围成一个圆柱体的粮囤(接头部分不计).用(?? )做底面周长,围成的粮囤容积大.
A.?长????????????????????????????????????????????????B.?宽
3.把棱长是2分米的正方体木块,削成一个最大的圆柱,这个圆柱的体积是(?? )立方分米.
A.?6.28???????????????????????????????????/B.?12.56???????????????????????????????????/C.?28.26???????????????????????????????????/D.?3.14
4.高12厘米的圆锥形容器里装满了水,把这些水全部倒入与它等底等高的圆柱形量杯内,水面高( )厘米.(容器厚度忽略不计)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?12
5.一块圆柱形橡皮泥,能捏成( )个和它等底等高的圆锥形橡皮泥.
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
6.一个圆柱的高是底面直径的π倍,这个圆柱侧面的展开图是一个( )
A.?平行四边形???????????????????????????????/B.?正方形???????????????????????????????/C.?长方形???????????????????????????????/D.?圆形
7.一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是(? )立方分米.
A.?50.24????????????????????????????????????????/B.?100.48????????????????????????????????????????/C.?64
二、判断题
8.一个圆柱与一个圆锥,它们的底面积和体积都相等.那么圆锥的高是圆柱高的 /.
9.把一个圆柱体削成一个与它等底等高的圆锥体,这个圆锥体的体积是削去部分的50%。
10.如果圆锥的底面积是圆柱底面积的3倍,则圆锥和圆柱的体积相等.
11.圆锥的底面积越大,它的体积一定就越大.
12.两个圆锥的底和高各不相等,则两个圆锥的体积也一定不相等。
三、填空题
13.一根圆柱形钢材,长1米,横截面直径1厘米,这根钢材的体积是________立方厘米?如果每立方厘米钢重7.8克,这根钢材重________克?(得数保留整数)
14.体育馆里的圆柱形状的柱子,底面周长2.5米,高5.2米.如果在柱子的侧面涂上油漆,每根柱子涂油漆的面积是________平方米?
15.一个圆柱体的底面直径4分米,高0.5分米,它的侧面积是________平方分米;它的表面积是________平方分米;它的体积是________立方分米.
16.圆柱的两个底面是两个大小________的圆,如果一个圆柱的底面周长和高相等,那么它的侧面展开是一个________。
17.一个圆柱和一个圆锥等底等高,它们的体积之和是48立方分米,那么圆锥的体积是________立方分米,圆柱的体积是________立方分米。
18.把一个圆柱削成一个最大的圆锥,那么圆锥的体积是削去部分体积的________。
四、计算题
19.求下列图形的体积。(单位:dm)
(1)/
(2)/
五、解答题
20.一个无盖的圆柱形铁皮水桶,底面周长是12.56dm,高是5dm。做这个水桶至少要用铁皮多少平方分米?
21.在下图中分别标出圆柱和圆锥底面半径和高.
/
六、应用题
22.一个圆锥形沙堆,底面直径是6米,高是2.5米.用一辆载重8吨的汽车运,几次可以运完?(每立方米的沙重1.8吨,得数保留整数.)
23.有一块正方体的木料,它的棱长是6dm,把这块木料加工成一个最大的圆锥,这个圆锥的体积是多少?
答案解析部分
一、单选题
1.【答案】C
【解析】解答:由题意可知,设圆柱的体积、圆锥的体积分别是 /,由题意可知: /
分析:圆锥的体积公式和圆柱的体积公式。
2.【答案】A
【解析】【解答】圆柱的底面周长越长,这个圆柱的底面半径就越长,体积就越大。 故答案为:A。 【分析】根据题干分析可得,有两种不同的围法:一种是以6.28分米为底面周长,4分米为高,另一种是以4分米为底面周长,6.28分米为高,据此利用圆柱的容积公式求出它们的容积即可解答。
3.【答案】A
【解析】【解答】解:根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,
圆柱的体积是:
3.14×(2÷2)2×2
=3.14×1×2
=6.28(立方分米).
答:这个圆柱的体积是6.28立方分米.
故选:A.
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的体积公式计算即可.
4.【答案】B
【解析】【解答】解:倒入前后的水体积相同,等底等高的圆柱的体积是圆锥的体积的3倍,
所以把水全部倒入圆柱形量杯内,水的体积只占了圆柱形量杯的 /,所以水的高度也是占了整个量杯高度的 /;
已知量杯的高度为12厘米,所以水的高度是:12× /=4(厘米).
故选:B.
【分析】倒入前后的水体积相同,等底等高的圆柱的体积是圆锥的体积的3倍,所以把水全部倒入圆柱形量杯内,水的体积只占了圆柱形量杯的 /,所以水的高度也是占了整个量杯高度的 /,已知量杯的高度为12厘米,由此即可求得水的高度.
5.【答案】C
【解析】【解答】解:根据等底等高的圆锥形的体积是圆柱形体积的 /,
又因为,在捏橡皮泥的过程中,它的总体积不变,
所以能捏成3个和它等底等高的圆锥形橡皮泥,
故选:C.
【分析】根据题意知道,在捏橡皮泥的过程中,它的总体积不变,再根据等底等高的圆锥形和圆柱形的关系,即可得到答案.
6.【答案】B
【解析】【解答】解:因为圆柱的底面周长C=πd,圆柱的高h=πd,
则这个圆柱的底面周长和高相等,即展开后的长方形的长和宽相等,
所以说这个圆柱侧面的展开图是一个正方形;
故选:B.
【分析】根据“圆柱的侧面展开后是长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高”可知:圆柱的底面周长C=πd,由“一个圆柱的高是底面直径的π倍”可得:圆柱的高h=πd,则这个圆柱的底面周长和高相等,即展开后的长方形的长和宽相等,所以说这个圆柱侧面的展开图是一个正方形.
7.【答案】A
【解析】【解答】解:3.14×(4÷2)2×4,
=3.14×22×4,
=3.14×4×4,
=50.24(立方分米);
答:体积是50.24立方分米.
故答案为50.24.
【分析】要求圆柱体的体积,须知道圆柱的底面半径和圆柱的高,从一个棱长4分米的正方体木块削成一个最大的圆柱体,可知圆柱的高和底面直径都是4分米,由此问题得解.此题主要考查圆柱体的体积计算公式:V=πr2h,解答时一定要注意分清题目中条件,灵活解答.
二、判断题
8.【答案】错误
【解析】【解答】设圆柱和圆锥的体积都是V,底面积都是S,则 圆柱的高是:V÷S=/, 圆锥的高是:3V÷S=/, /÷/=3,原题说法错误. 故答案为:错误.
【分析】根据题意,设圆柱和圆锥的体积都是V,底面积都是S,分别表示出圆柱和圆锥的高,然后相除即可解答.
9.【答案】正确
【解析】解答:设圆柱的体积、圆锥的体积和削去部分的体积分别是 /,因为削出的圆锥与圆柱等底等高,所以 /。
分析:等底等高的圆柱的体积、圆锥的体积及削去部分的体积之间的关系。
10.【答案】错误
【解析】【解答】圆柱和圆锥的高不确定,无法确定圆柱和圆锥的体积,原题说法错误. 故答案为:错误 【分析】圆柱和圆锥的体积与底面积和高的大小有关,只确定底面积,不确定高,就无法确定体积的大小.
11.【答案】错误
【解析】【解答】圆锥的高不确定,无法确定体积的大小;原题说法错误. 故答案为:错误 【分析】圆锥的体积与底面积和高的大小有关,只确定底面积,不确定高,就无法确定体积的大小.
12.【答案】错误
【解析】【解答】解:例如:一个圆锥底面积是10高是3,体积是10;另一个圆锥底面积是5,高是6,体积也是10;原题说法错误. 故答案为:错误
【分析】圆锥的体积=底面积×高×/,圆锥的底面积和高不相等,并不能说明两个圆锥的体积不相等.
三、填空题
13.【答案】79;612
【解析】【解答】1米=100厘米 3.14×(1÷2)2×100 =3.14×0.25×100 ≈79(立方厘米) 78.5×7.8≈612(克) 【分析】首先统一单位把1米化成100厘米,然后根据圆柱的体积=底面积×高求出钢材的体积,再用钢材的体积乘每立方厘米钢重量即可。
14.【答案】13
【解析】【解答】2.5×5.2=13(平方米) 【分析】此题重点考查圆柱体的侧面积公式s=ch的掌握与运用情况,解答此题应注意分清求的是几个面的面积,据此列式计算即可。
15.【答案】6.28;31.4;6.28
【解析】【解答】解:(1)圆柱的侧面积为:3.14×4×0.5 =12.56×0.5, =6.28(平方分米);(2)圆柱的底面半径为:4÷2=2(分米), 圆柱的表面积为:3.14×22×2+6.28 =12.56×2+6.28, =25.12+6.28, =31.4(平方分米);(3)圆柱的体积为:3.14×22×0.5 =12.56×0.5, =6.28(立方分米); 答:圆柱的侧面积是6.28平方分米,表面积为31.4平方分米,圆柱的体积是6.28立方分米. 故答案为:6.28,31.4,6.28. 【分析】根据题意,可利用圆柱体的侧面积=底面周长×高,圆柱的表面积=侧面积+两个底面的面积,圆柱的体积=底面积×高进行计算即可得到答案.
16.【答案】相等;正方形
【解析】【解答】解:根据圆柱的特征可知,圆柱的两个底面是两个大小相等的圆,如果一个圆柱的底面周长和高相等,那么它的侧面展开是一个正方形. 故答案为:相等;正方形 【分析】圆柱的上下两个底面大小相等,侧面是一个曲面,侧面展开后是一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,另一条边与高相等;如果底面周长和高相等,侧面展开就是一个正方形.
17.【答案】12 ;36
【解析】【解答】解:48÷(3+1)=12(立方分米),圆锥体积是12立方分米,圆柱体积为:12×3=36(立方分米). 故答案为:12;36.
【分析】等底等高的圆柱体积是圆锥体积的3倍,再用体积和除以(3+1)求出一份是多少,再用3乘12求出圆柱体积.
18.【答案】/
【解析】【解答】解:削成的圆锥体积是1,圆柱的体积是3,圆锥的体积是削去部分体积的:1÷(3-1)=/. 故答案为:/
【分析】等底等高的圆柱体积是圆锥体积的3倍,因此削成的最大圆锥体积是1,圆柱的体积就是3,削去的部分是(3-1);用圆锥的体积除以削去部分的体积即可.
四、计算题
19.【答案】(1)πr2h=3.14×82×10=2009.6(dm3) (2)/πr2h=/×3.14× 2×24=2512(dm3)
【解析】【分析】根据圆柱的体积公式V=sh=πr2h,圆锥的体积公式V=?/sh=/πr2h,代入数据即可求解。
五、解答题
20.【答案】解:(12.56÷3.14÷2)2×3.14+12.56×5 =4×3.14+62.8 =12.56+62.8 =75.36(dm2)
答:做这个水桶至少要用铁皮75.36平方分米.
【解析】【分析】用底面周长除以3.14再除以2求出底面半径,然后用底面积加上侧面积即可求出需要铁皮的面积,圆柱的侧面积=底面周长×高.
21.【答案】/
【解析】【分析】圆柱的上下两个面叫做底面,它们是完全相同的两个圆,两个底之间的距离是圆柱的高,可以将两个圆的圆心相连即可得到高,底面圆的半径是圆柱的底面半径,连接圆锥的顶点和底面圆心的线段是圆锥的高,底面圆的半径是圆锥的底面半径,据此解答.
六、应用题
22.【答案】解: /×3.14×(6÷2)2×2.5×1.8÷8, =9.42×2.5×1.8÷8, =23.55×1.8÷8, =42.39÷8, ≈6(次), 答:6次可以运完
【解析】【分析】根据圆锥的体积公式V= /sh,求出圆锥形沙堆的体积,进而求出沙堆的重量,最后用沙堆的重量除以8吨就是要求的答案.
23.【答案】解: /
= /
=56.52(立方分米),
答:这个圆锥的体积是56.52立方分米
【解析】【分析】根据题意可知:把棱长是6分米的正方体木料加工成一个最大的圆锥,这个圆锥的底面直径和高都等于正方体的棱长,根据圆锥的体积公式:v= /,把数据代入公式解答.
