三 解决问题的策略 课件(36张PPT)
文档属性
| 名称 | 三 解决问题的策略 课件(36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-16 00:00:00 | ||
图片预览







文档简介
解决问题的策略
教学目标
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。
教学重、难点
教学重点:感受“转化”策略的价值,会用“转化”的策略解决问题,丰富学生的策略意识。
教学难点:掌握转化的方法和技巧,会用“转化”的策略解决问题。
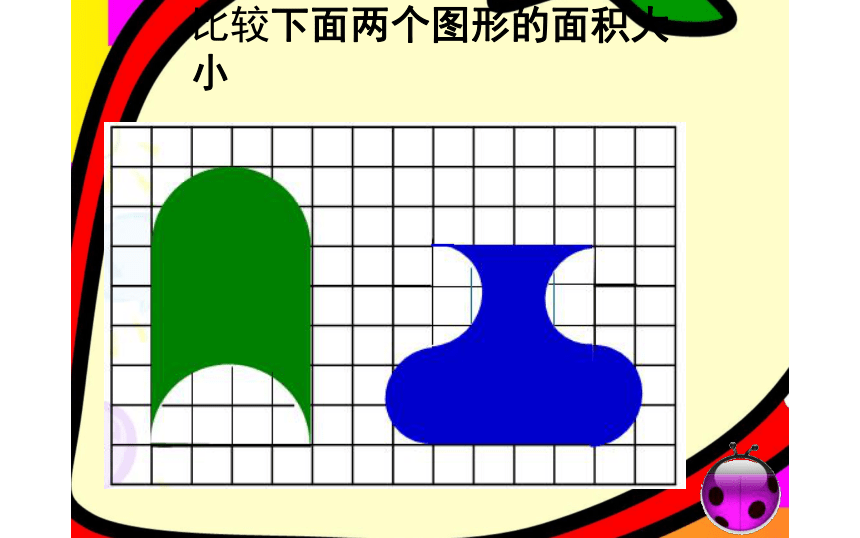
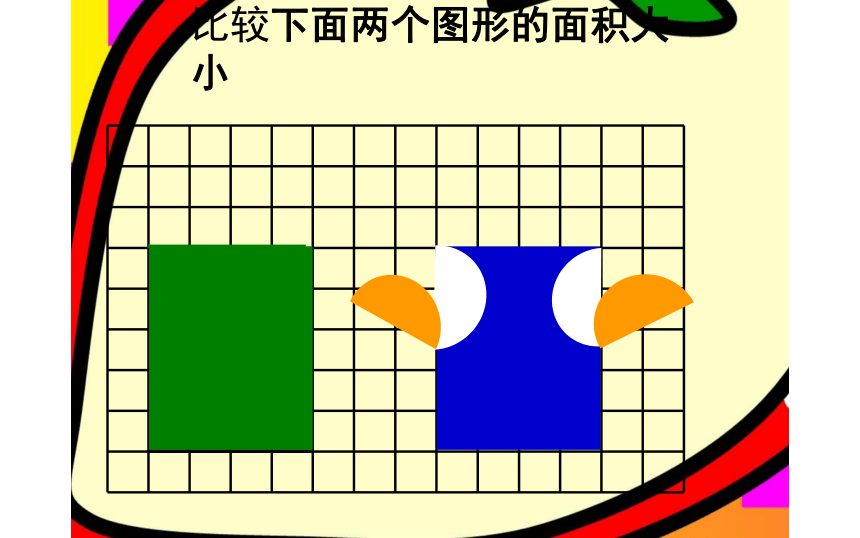
观察与思考:
比较下面两个图形的面积大小
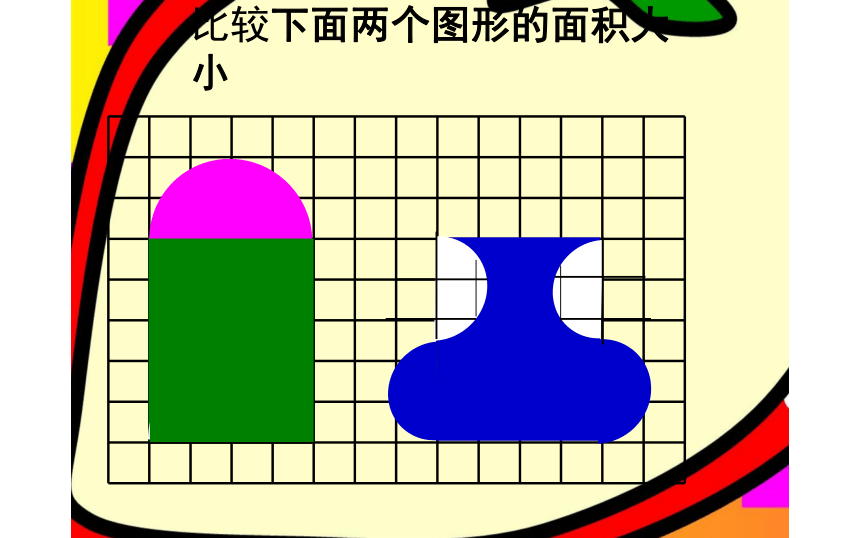
观察与思考:
比较下面两个图形的面积大小
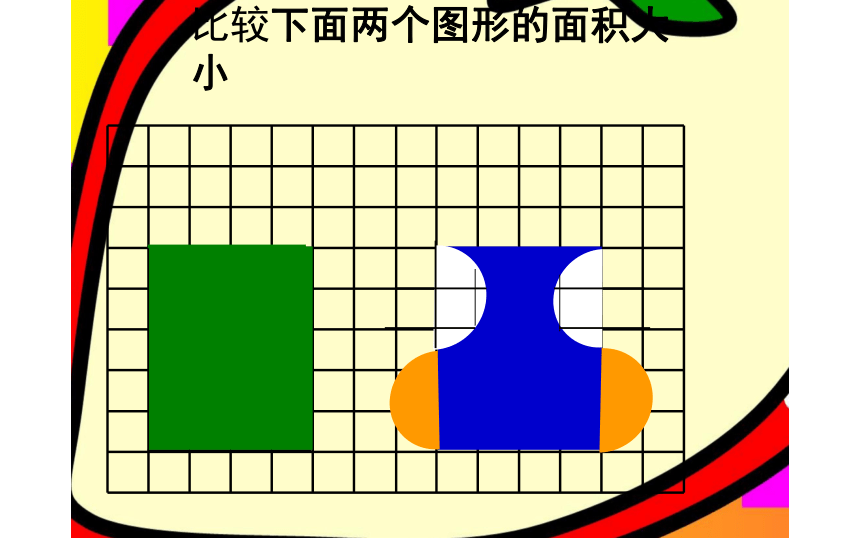
观察与思考:
比较下面两个图形的面积大小
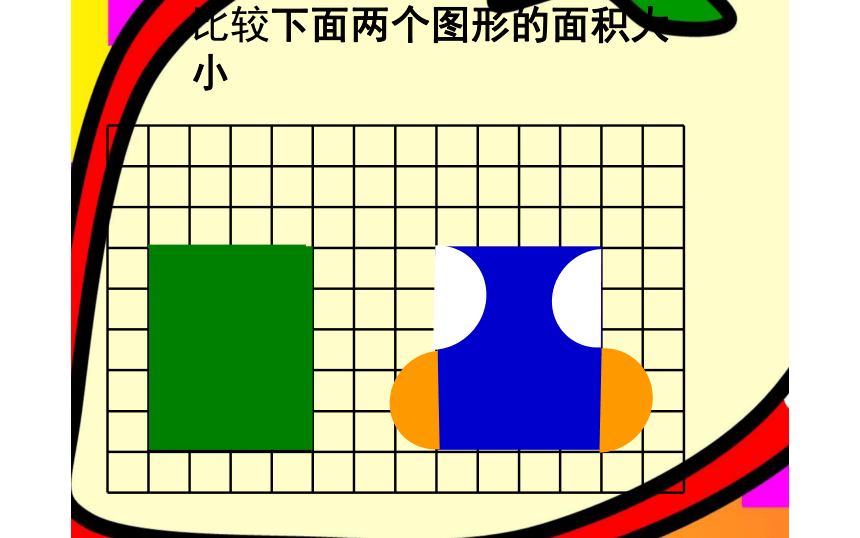
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
回顾一下,我们曾经运用转化的策略解决过哪些问题?
三化平
异化同
除化乘
策略一
柱化长
圆化长
推导平行四边形的面积公式时,把平行四边形转化成长方形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
计算圆的面积时,把圆转化成长方形。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9
10
11
12
13
14
15
16
计算圆柱的体积时,把圆柱转化成长方体。
平化长
三化平
异化同
除化乘
柱化长
圆化长
计算异分母分数加减法时,把异分母分数转化成同分母分数。
平化长
三化平
异化同
除化乘
柱化长
圆化长
计算分数除法时,把分数除法转化成分数乘法。
3
2
7
2
×
÷
=
3
2
2
7
5
2
4
1
×
÷
=
5
2
4
平化长
三化平
异化同
除化乘
柱化长
圆化长
策略一
可以把原式转化成怎样的算式计算?
2
1
4
1
+
+
+
8
1
计算
16
1
2
1
4
1
8
1
1--=-
16
1
16
15
2
1
4
1
+
+
+
8
1
计算
16
1
策略一
2
1
4
1
8
1
应用一
计算:1+3+5+7+9+11+13=
46
应用二
19.96÷2 -0.4×9.96 =?
1
2
答案:4
上页
应用三
有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
8
4
2
1
8+4+2+1=15 (场)
策略三
或 16 – 1 = 15(场)
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
在一个等边三角形中画一个尽可能大的圆,又在这个圆中画一个尽可能大的等边三角形(如图)。问,图中小等边三角形的面积相当于大等边三角形面积的几分之几?
答案:
1
4
用转化的策略解决问题
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。
用转化的策略解决问题
!
?
不规则--规则
新知---旧知
数字---图形
复杂---简单
教学目标
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。
教学重、难点
教学重点:感受“转化”策略的价值,会用“转化”的策略解决问题,丰富学生的策略意识。
教学难点:掌握转化的方法和技巧,会用“转化”的策略解决问题。
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
回顾一下,我们曾经运用转化的策略解决过哪些问题?
三化平
异化同
除化乘
策略一
柱化长
圆化长
推导平行四边形的面积公式时,把平行四边形转化成长方形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
平化长
三化平
异化同
除化乘
柱化长
圆化长
推导三角形的面积公式时,把三角形转化成平行四边形。
计算圆的面积时,把圆转化成长方形。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9
10
11
12
13
14
15
16
计算圆柱的体积时,把圆柱转化成长方体。
平化长
三化平
异化同
除化乘
柱化长
圆化长
计算异分母分数加减法时,把异分母分数转化成同分母分数。
平化长
三化平
异化同
除化乘
柱化长
圆化长
计算分数除法时,把分数除法转化成分数乘法。
3
2
7
2
×
÷
=
3
2
2
7
5
2
4
1
×
÷
=
5
2
4
平化长
三化平
异化同
除化乘
柱化长
圆化长
策略一
可以把原式转化成怎样的算式计算?
2
1
4
1
+
+
+
8
1
计算
16
1
2
1
4
1
8
1
1--=-
16
1
16
15
2
1
4
1
+
+
+
8
1
计算
16
1
策略一
2
1
4
1
8
1
应用一
计算:1+3+5+7+9+11+13=
46
应用二
19.96÷2 -0.4×9.96 =?
1
2
答案:4
上页
应用三
有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
8
4
2
1
8+4+2+1=15 (场)
策略三
或 16 – 1 = 15(场)
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
2厘米
2厘米
挑战、求阴影部分的面积。
在一个等边三角形中画一个尽可能大的圆,又在这个圆中画一个尽可能大的等边三角形(如图)。问,图中小等边三角形的面积相当于大等边三角形面积的几分之几?
答案:
1
4
用转化的策略解决问题
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。
用转化的策略解决问题
!
?
不规则--规则
新知---旧知
数字---图形
复杂---简单
