六年级下册数学课件-总复习 1.7 计算与应用(2)_北师大版(2014秋)(共16张PPT)
文档属性
| 名称 | 六年级下册数学课件-总复习 1.7 计算与应用(2)_北师大版(2014秋)(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 782.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-15 21:21:49 | ||
图片预览






文档简介
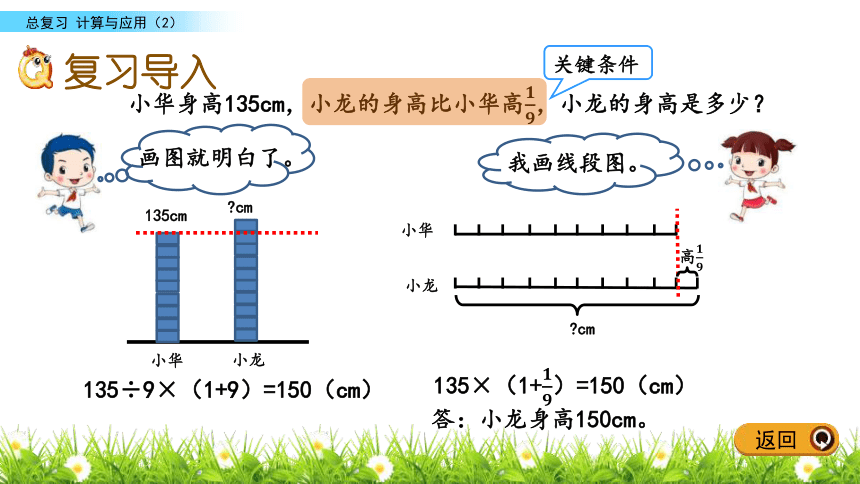
课件16张PPT。计算与应用(2)总复习复习导入巩固练习课后作业知识梳理?小华小龙135cm?cm小华小龙? ?cm关键条件135÷9×(1+9)=150(cm)?答:小龙身高150cm。复习导入在解决实际问题中 ,画图能帮助我们分析数量关系。●读懂题目很重要。●还要找到题目中的数量关系哟!●选择解决问题的方法,列式并计算。●别忘了还要对答案进行检验,看它是否符合实际。1.分数、百分数应用题分数、百分数应用题方法实质是一样的。知识梳理2.比例尺问题1.比例尺:图上距离和实际距离的比。3.比例尺的分类:数值比例尺和线段比例尺。
扩大比例尺和缩小比例尺。图上距离=实际距离×比例尺实际距离=图上距离÷比例尺3.打折问题几折就是十分之几,也就是百分之几十。
商品现价 = 商品原价 × 折数
原价=商品现价÷折数例题:一种衣服原价每件50元,现在打九折出售,每件售价多少元?50×0.9=45(元)答:每件售价45元。4.按比例分配问题例题:师傅和徒弟一共加工了72个零件,师傅加工的零件个数和徒弟加工的零件个数的比是5:3,师傅和徒弟各加工了多少个零件???一共分成5+3=8份或72÷8×5=45(个)或72÷8×3=27(个)答:师傅加工了45个,徒弟加工了27个。师傅:徒弟:根据速度、时间和路程三者之间的关系,计算相向、相背和同向运动的问题,叫做行程问题。1.同时同地相背而行:路程=速度和×时间。始终围绕这三个量之间的关系2.同时相向而行:相遇时间=两地路程÷速度和 3.同时同向而行(速度慢的在前,快的在后):
追及时间=两地路程÷速度差4.同时同地同向而行(速度慢的在后,快的在前):
路程相差=速度差×时间 5.行程问题6.工程问题主要研究工作总量、工作效率和工作时间三个量之间的关系。
工作总量=工作效率×工作时间 工作效率=工作总量÷工作时间 工作时间=工作总量÷工作效率已知工地有一堆黄沙重120吨,第一天运走了它的25%,第二天运走了剩下黄沙的 20%。
(1)第一天运走了多少吨?
(2)第二天运走了多少吨?
(3)第一天比第二天多运走多少吨?
(4)两天一共运走了多少吨?
(5)还剩下多少吨?
120×25%=30(吨)
(120-30)×20%=18(吨)
30-18=12(吨)
30+18=48(吨)
120-48=72(吨)一堆黄沙是单位“1”的量单位“1”的量是剩下黄沙巩固练习六年级男生有180人,女生有160人,男生比女生多百分之几?女生比男生少百分之几?
女生是单位“1”的量男生是单位“1”的量(180-160)÷160 =12.5%(180-160)÷180 ≈11.1% 答:男生比女生多12.5%,女生比男生少11.1%。在比例尺是1:60000的地图上,量得甲、乙两地的距离是2.5厘米。两地的实际距离是多少千米?2.5厘米×60000 =150000厘米 =1.5千米
答:实际距离是1.5千米。一种精密零件,画在图上是12厘米,而实际的长度是3毫米。求这幅图的比例尺。
12cm=120mm 比例尺120:3=40:1答:这幅图的比例尺是40:1。有一个公园原来的门票是80元,国庆期间打八折,每张门票能节省多少元?相当于降价了百分之几?80×(1-80%)=16(元)
降价了1-80%=20%答:节省16元,降价20%。建筑工人配制一种混凝土,水泥、沙子和石子的比是2:3:5,已知用了1500千克石子,需要水泥 沙子各多少千克?水泥:1500÷5×2=600(千克)
沙子:1500÷5×3=900(千克)答:水泥600千克,沙子900千克。甲在乙的后面 28 千米 ,两人同时同向而行,甲每小时行 16 千米 ,乙每小时行 9 千米 ,甲几小时追上乙? 28÷(16-9)=4(小时) 答:甲4小时可以追上乙。每小时可以追7千米修一条长1960米的路,先是每天修80米,修了8天以后为了尽快完成任务,以后打算每天修120米,还要多少天才能修完?(1960-80×8)÷120=11(天)答:还要修11天才能修完。一项工程甲队单独完成需要12天,乙队单独完成需要15天,甲、乙两队共同工作5天后,剩下的由甲队单独去做,还需要几天完成?
????答:还需要3天才能完成。课本:
第74页第5、6、7题。课后作业
扩大比例尺和缩小比例尺。图上距离=实际距离×比例尺实际距离=图上距离÷比例尺3.打折问题几折就是十分之几,也就是百分之几十。
商品现价 = 商品原价 × 折数
原价=商品现价÷折数例题:一种衣服原价每件50元,现在打九折出售,每件售价多少元?50×0.9=45(元)答:每件售价45元。4.按比例分配问题例题:师傅和徒弟一共加工了72个零件,师傅加工的零件个数和徒弟加工的零件个数的比是5:3,师傅和徒弟各加工了多少个零件???一共分成5+3=8份或72÷8×5=45(个)或72÷8×3=27(个)答:师傅加工了45个,徒弟加工了27个。师傅:徒弟:根据速度、时间和路程三者之间的关系,计算相向、相背和同向运动的问题,叫做行程问题。1.同时同地相背而行:路程=速度和×时间。始终围绕这三个量之间的关系2.同时相向而行:相遇时间=两地路程÷速度和 3.同时同向而行(速度慢的在前,快的在后):
追及时间=两地路程÷速度差4.同时同地同向而行(速度慢的在后,快的在前):
路程相差=速度差×时间 5.行程问题6.工程问题主要研究工作总量、工作效率和工作时间三个量之间的关系。
工作总量=工作效率×工作时间 工作效率=工作总量÷工作时间 工作时间=工作总量÷工作效率已知工地有一堆黄沙重120吨,第一天运走了它的25%,第二天运走了剩下黄沙的 20%。
(1)第一天运走了多少吨?
(2)第二天运走了多少吨?
(3)第一天比第二天多运走多少吨?
(4)两天一共运走了多少吨?
(5)还剩下多少吨?
120×25%=30(吨)
(120-30)×20%=18(吨)
30-18=12(吨)
30+18=48(吨)
120-48=72(吨)一堆黄沙是单位“1”的量单位“1”的量是剩下黄沙巩固练习六年级男生有180人,女生有160人,男生比女生多百分之几?女生比男生少百分之几?
女生是单位“1”的量男生是单位“1”的量(180-160)÷160 =12.5%(180-160)÷180 ≈11.1% 答:男生比女生多12.5%,女生比男生少11.1%。在比例尺是1:60000的地图上,量得甲、乙两地的距离是2.5厘米。两地的实际距离是多少千米?2.5厘米×60000 =150000厘米 =1.5千米
答:实际距离是1.5千米。一种精密零件,画在图上是12厘米,而实际的长度是3毫米。求这幅图的比例尺。
12cm=120mm 比例尺120:3=40:1答:这幅图的比例尺是40:1。有一个公园原来的门票是80元,国庆期间打八折,每张门票能节省多少元?相当于降价了百分之几?80×(1-80%)=16(元)
降价了1-80%=20%答:节省16元,降价20%。建筑工人配制一种混凝土,水泥、沙子和石子的比是2:3:5,已知用了1500千克石子,需要水泥 沙子各多少千克?水泥:1500÷5×2=600(千克)
沙子:1500÷5×3=900(千克)答:水泥600千克,沙子900千克。甲在乙的后面 28 千米 ,两人同时同向而行,甲每小时行 16 千米 ,乙每小时行 9 千米 ,甲几小时追上乙? 28÷(16-9)=4(小时) 答:甲4小时可以追上乙。每小时可以追7千米修一条长1960米的路,先是每天修80米,修了8天以后为了尽快完成任务,以后打算每天修120米,还要多少天才能修完?(1960-80×8)÷120=11(天)答:还要修11天才能修完。一项工程甲队单独完成需要12天,乙队单独完成需要15天,甲、乙两队共同工作5天后,剩下的由甲队单独去做,还需要几天完成?
????答:还需要3天才能完成。课本:
第74页第5、6、7题。课后作业
