九年级下册数学27.2相似三角形助学案(表格式 5课时 无答案)
文档属性
| 名称 | 九年级下册数学27.2相似三角形助学案(表格式 5课时 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-15 00:00:00 | ||
图片预览

文档简介
课题 27.2.1相似三角形的判定(1) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握相似三角形的定义、三角形相似的预备定理及两个三角形相似的判定条件. 2、通过两个三角形相似条件的探索过程,进一步发展学生的探究、交流能力. 3、经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步发展同学们的探究、交流能力.
重点 两个三角形相似的判定方法1.
难点 探究判定方法1的过程.
学习过程 学(教)记录
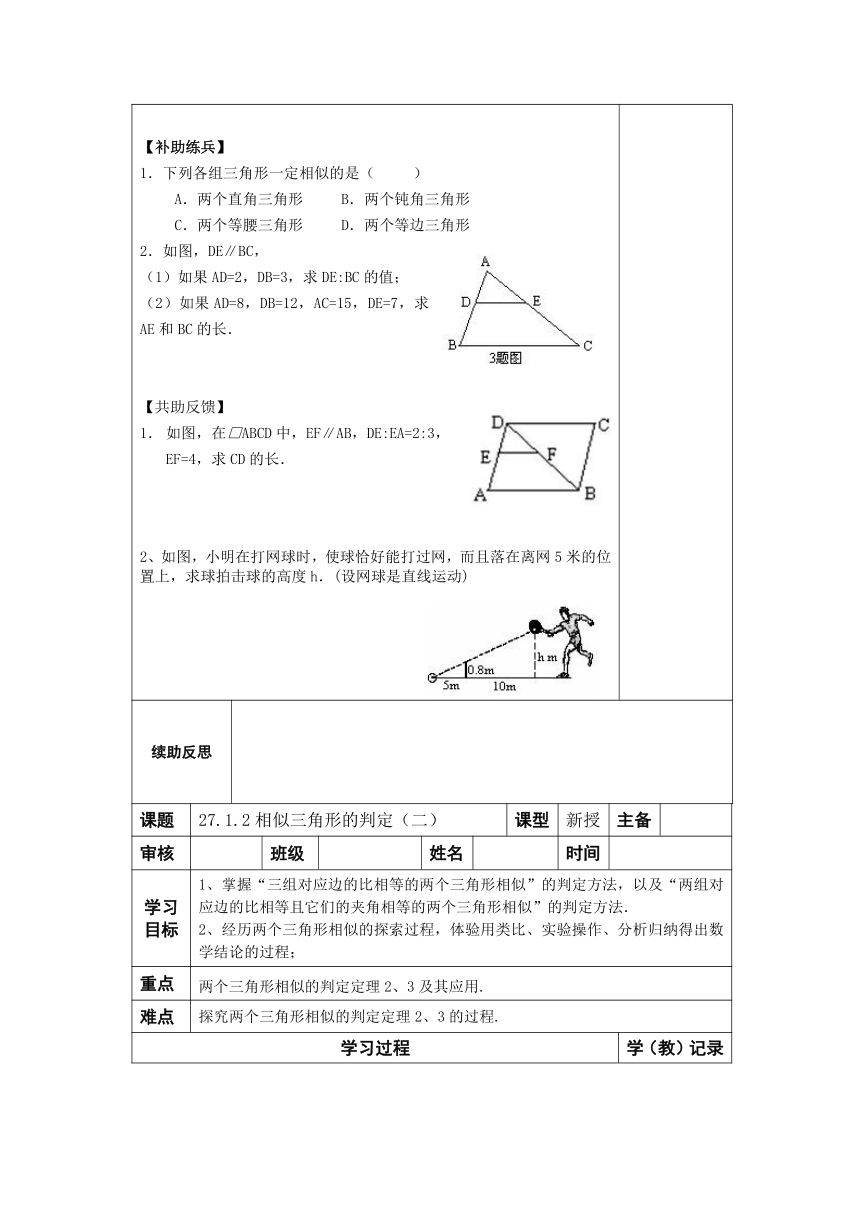
【自助学习】 (1)相似多边形的性质是什么? (2)在相似多边形中,最简单的就是相似三角形. 在△ABC与△A′B′C′中,如果 且 . 我们就说△ABC与△A′B′C′相似,记作 , 就是它们的相似比. 反之如果△ABC∽△A′B′C′,则有 且 . (3)如果k=1,这两个三角形有怎样的关系? 【互助探究】 1.课本P40的探究,动手量一量你能发现什么? 2.平行线分线度成比例定理: 3.平移其中的一条割线,你能发现什么? 4. 如图,DE∥BC,△ABC和△ADE相似吗? 由此你能得出三角形相似的判定吗? 【求助交流】 例1、如图△ABC∽△DCA,AD∥BC,∠B=∠DCA. (1)写出对应边的比例式 (2)写出所有相等的角 (3)若AB=10,BC=12,CA=6.求AD、DC的长. 例2、如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.?? 【补助练兵】 1.下列各组三角形一定相似的是( ) A.两个直角三角形 B.两个钝角三角形 C.两个等腰三角形 D.两个等边三角形 2.如图,DE∥BC, (1)如果AD=2,DB=3,求DE:BC的值; (2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长. 【共助反馈】 如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长. 2、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
续助反思
课题 27.1.2相似三角形的判定(二) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握“三组对应边的比相等的两个三角形相似”的判定方法,以及“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法. 2、经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;
重点 两个三角形相似的判定定理2、3及其应用.
难点 探究两个三角形相似的判定定理2、3的过程.
学习过程 学(教)记录
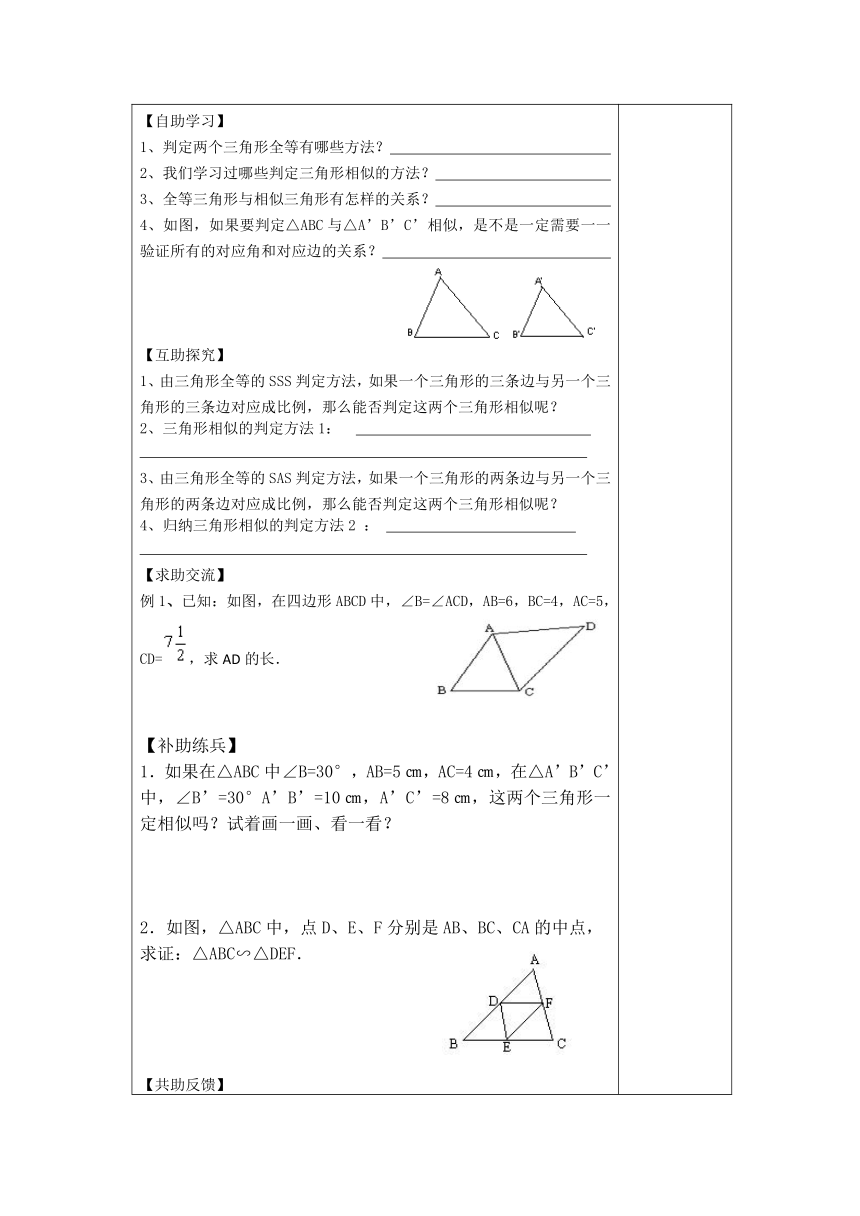
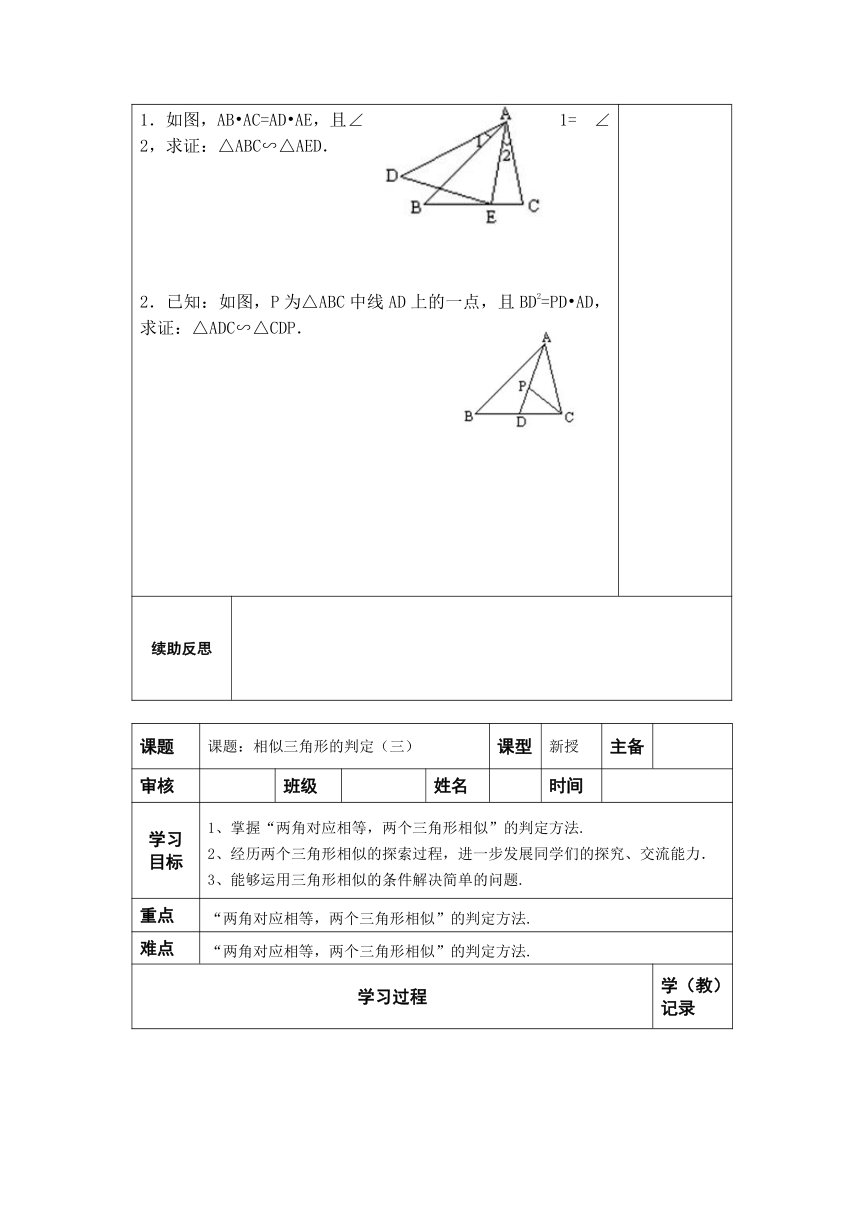
【自助学习】 1、判定两个三角形全等有哪些方法? 2、我们学习过哪些判定三角形相似的方法? 3、全等三角形与相似三角形有怎样的关系? 4、如图,如果要判定△ABC与△A’B’C’相似,是不是一定需要一一验证所有的对应角和对应边的关系? 【互助探究】 1、由三角形全等的SSS判定方法,如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么能否判定这两个三角形相似呢? 2、三角形相似的判定方法1: 3、由三角形全等的SAS判定方法,如果一个三角形的两条边与另一个三角形的两条边对应成比例,那么能否判定这两个三角形相似呢? 4、归纳三角形相似的判定方法2 : 【求助交流】 例1、已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=,求AD的长. 【补助练兵】 1.如果在△ABC中∠B=30°,AB=5㎝,AC=4㎝,在△A’B’C’中,∠B’=30°A’B’=10㎝,A’C’=8㎝,这两个三角形一定相似吗?试着画一画、看一看? 如图,△ABC中,点D、E、F分别是AB、BC、CA的中点, 求证:△ABC∽△DEF. 【共助反馈】 1.如图,AB?AC=AD?AE,且∠1=∠2,求证:△ABC∽△AED. 2.已知:如图,P为△ABC中线AD上的一点,且BD2=PD?AD,求证:△ADC∽△CDP.
续助反思
课题 课题:相似三角形的判定(三) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握“两角对应相等,两个三角形相似”的判定方法. 2、经历两个三角形相似的探索过程,进一步发展同学们的探究、交流能力. 3、能够运用三角形相似的条件解决简单的问题.
重点 “两角对应相等,两个三角形相似”的判定方法.
难点 “两角对应相等,两个三角形相似”的判定方法.
学习过程 学(教)记录
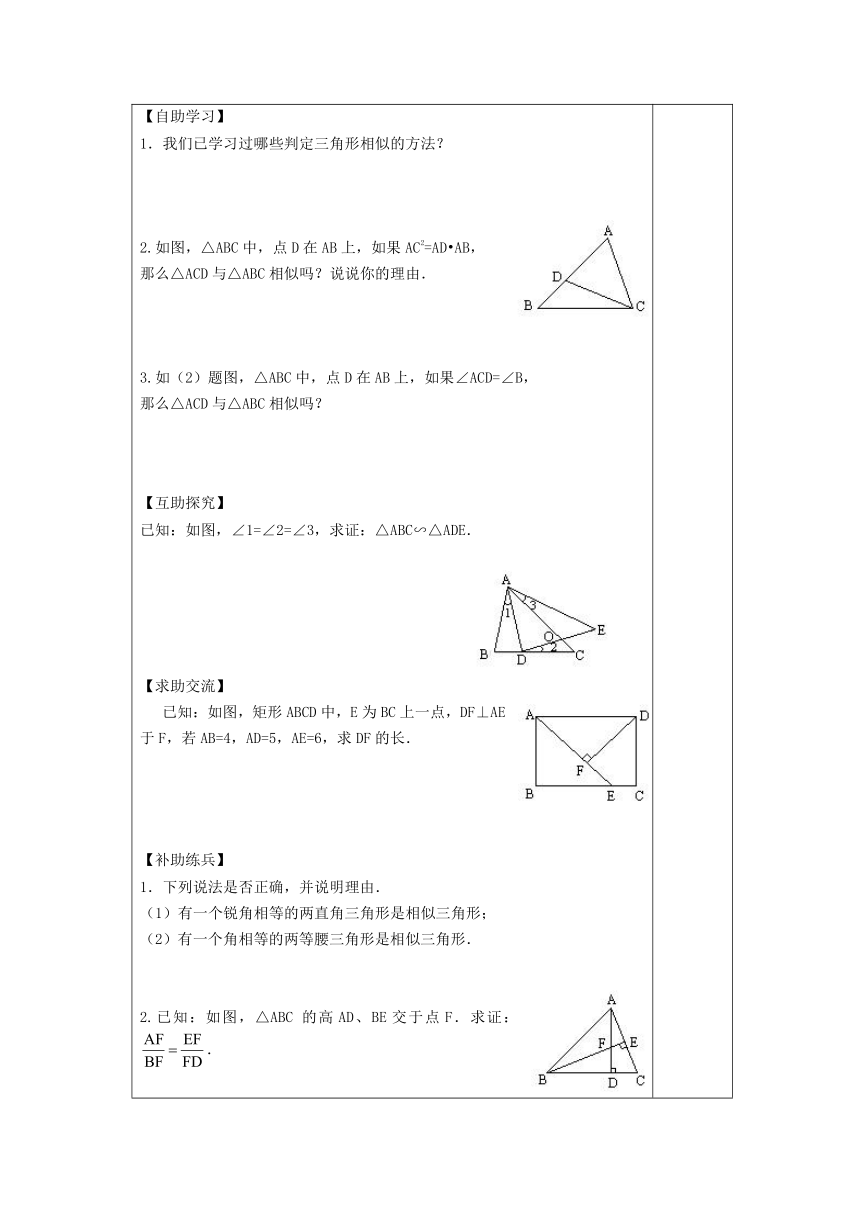
【自助学习】 1.我们已学习过哪些判定三角形相似的方法? 2.如图,△ABC中,点D在AB上,如果AC2=AD?AB, 那么△ACD与△ABC相似吗?说说你的理由. 3.如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B, 那么△ACD与△ABC相似吗? 【互助探究】 已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE. 【求助交流】 已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长. 【补助练兵】 1.下列说法是否正确,并说明理由. (1)有一个锐角相等的两直角三角形是相似三角形; (2)有一个角相等的两等腰三角形是相似三角形. 2.已知:如图,△ABC 的高AD、BE交于点F.求证:. 【共助反馈 】 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高. (1)求证:AC?BC=BE?CD; (2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
续助反思
课题 27.2.2相似三角形的应用举例 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、能够运用三角形相似的知识,解决一些实际问题. 2、通过把实际问题转化成相似三角形的数学模型,进一步了解数学建模的思想. 3、通过解决实际问题,培养学生分析问题、解决问题的能力.
重点 运用三角形相似的知识解决实际问题.
难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题).
学习过程 学(教)记录
【自助学习】 1、判断两三角形相似有哪些方法? 2、相似三角形有什么性质? 【互助探究】 据史料记载,古希腊数学家、天文学家泰勒斯曾经利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成的两个相似三角形来测量金字塔的高度.如图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO. 【求助交流】 如图,为了估算河的宽度,我们可以在河对岸选定一个目标P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS = 45 m,ST = 90 m,QR = 60 m,求河的宽度PQ. 【补助练兵】 已知左、右并排的两棵大树的高分别是AB = 8 m和CD = 12 m,两树根部的距离BD = 5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C? 【共助反馈】 在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米? 小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高? 3.小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
续助反思
课题 27.2.3相似三角形的周长与面积 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、理解并初步掌握相似三角形周长与面积的性质. 2、通过把实际问题转换化成数学模型,体会从特殊到一般的认识问题的方法. 3、通过对性质的发现和论证,提高数学学习热情,增强探究意识.
重点 相似三角形的性质与运用.
难点 相似三角形性质的灵活运用.
学习过程 学(教)记录
【自助学习】 已知: ?ABC∽?A’B’C’,根据相似的定义,我们有哪些结论? 问:两个三角形相似,除了对应边成比例、对应角相等之外,我们还可以得到哪些结论? 2.思考:(1)如果两个三角形相似,它们的周长之间有什么关系? (2)如果两个三角形相似,它们的面积之间有什么关系? (3)两个相似多边形的周长和面积分别有什么关系? 【互助探究】 已知:如图:△ABC ∽△A′B′C′,它们的周长分别是 60 cm 和72 cm,且AB=15 cm,B′C′=24 cm,求BC、AB、A′B′、A′C′的长. 【求助交流】 在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是12,求ΔDEF的周长和面积。 【补助练兵】 1.填空: (1)如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为_____,面积的比为_____. (2)如果两个相似三角形面积的比为3∶5 ,那么它们的相似比为________,周长的比为________. (3)连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______. (4)两个相似三角形对应的中线长分别是6 cm和18 cm,若较大 三角形的周长是42 cm ,面积是12 cm 2,则较小三角形的周长为________cm,面积为_______cm2. 2.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比. 【共助反馈】已知:如图,△ABC中,DE∥BC,
(1)若,① 求的值; ② 求的值; ③ 若,求△ADE的面积; (2)若,,过点E作EF∥AB交BC于F,求□BFED的面积;
续助反思
审核 班级 姓名 时间
学习 目标 1、掌握相似三角形的定义、三角形相似的预备定理及两个三角形相似的判定条件. 2、通过两个三角形相似条件的探索过程,进一步发展学生的探究、交流能力. 3、经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步发展同学们的探究、交流能力.
重点 两个三角形相似的判定方法1.
难点 探究判定方法1的过程.
学习过程 学(教)记录
【自助学习】 (1)相似多边形的性质是什么? (2)在相似多边形中,最简单的就是相似三角形. 在△ABC与△A′B′C′中,如果 且 . 我们就说△ABC与△A′B′C′相似,记作 , 就是它们的相似比. 反之如果△ABC∽△A′B′C′,则有 且 . (3)如果k=1,这两个三角形有怎样的关系? 【互助探究】 1.课本P40的探究,动手量一量你能发现什么? 2.平行线分线度成比例定理: 3.平移其中的一条割线,你能发现什么? 4. 如图,DE∥BC,△ABC和△ADE相似吗? 由此你能得出三角形相似的判定吗? 【求助交流】 例1、如图△ABC∽△DCA,AD∥BC,∠B=∠DCA. (1)写出对应边的比例式 (2)写出所有相等的角 (3)若AB=10,BC=12,CA=6.求AD、DC的长. 例2、如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.?? 【补助练兵】 1.下列各组三角形一定相似的是( ) A.两个直角三角形 B.两个钝角三角形 C.两个等腰三角形 D.两个等边三角形 2.如图,DE∥BC, (1)如果AD=2,DB=3,求DE:BC的值; (2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长. 【共助反馈】 如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长. 2、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
续助反思
课题 27.1.2相似三角形的判定(二) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握“三组对应边的比相等的两个三角形相似”的判定方法,以及“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法. 2、经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;
重点 两个三角形相似的判定定理2、3及其应用.
难点 探究两个三角形相似的判定定理2、3的过程.
学习过程 学(教)记录
【自助学习】 1、判定两个三角形全等有哪些方法? 2、我们学习过哪些判定三角形相似的方法? 3、全等三角形与相似三角形有怎样的关系? 4、如图,如果要判定△ABC与△A’B’C’相似,是不是一定需要一一验证所有的对应角和对应边的关系? 【互助探究】 1、由三角形全等的SSS判定方法,如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么能否判定这两个三角形相似呢? 2、三角形相似的判定方法1: 3、由三角形全等的SAS判定方法,如果一个三角形的两条边与另一个三角形的两条边对应成比例,那么能否判定这两个三角形相似呢? 4、归纳三角形相似的判定方法2 : 【求助交流】 例1、已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=,求AD的长. 【补助练兵】 1.如果在△ABC中∠B=30°,AB=5㎝,AC=4㎝,在△A’B’C’中,∠B’=30°A’B’=10㎝,A’C’=8㎝,这两个三角形一定相似吗?试着画一画、看一看? 如图,△ABC中,点D、E、F分别是AB、BC、CA的中点, 求证:△ABC∽△DEF. 【共助反馈】 1.如图,AB?AC=AD?AE,且∠1=∠2,求证:△ABC∽△AED. 2.已知:如图,P为△ABC中线AD上的一点,且BD2=PD?AD,求证:△ADC∽△CDP.
续助反思
课题 课题:相似三角形的判定(三) 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、掌握“两角对应相等,两个三角形相似”的判定方法. 2、经历两个三角形相似的探索过程,进一步发展同学们的探究、交流能力. 3、能够运用三角形相似的条件解决简单的问题.
重点 “两角对应相等,两个三角形相似”的判定方法.
难点 “两角对应相等,两个三角形相似”的判定方法.
学习过程 学(教)记录
【自助学习】 1.我们已学习过哪些判定三角形相似的方法? 2.如图,△ABC中,点D在AB上,如果AC2=AD?AB, 那么△ACD与△ABC相似吗?说说你的理由. 3.如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B, 那么△ACD与△ABC相似吗? 【互助探究】 已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE. 【求助交流】 已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长. 【补助练兵】 1.下列说法是否正确,并说明理由. (1)有一个锐角相等的两直角三角形是相似三角形; (2)有一个角相等的两等腰三角形是相似三角形. 2.已知:如图,△ABC 的高AD、BE交于点F.求证:. 【共助反馈 】 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高. (1)求证:AC?BC=BE?CD; (2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
续助反思
课题 27.2.2相似三角形的应用举例 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、能够运用三角形相似的知识,解决一些实际问题. 2、通过把实际问题转化成相似三角形的数学模型,进一步了解数学建模的思想. 3、通过解决实际问题,培养学生分析问题、解决问题的能力.
重点 运用三角形相似的知识解决实际问题.
难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题).
学习过程 学(教)记录
【自助学习】 1、判断两三角形相似有哪些方法? 2、相似三角形有什么性质? 【互助探究】 据史料记载,古希腊数学家、天文学家泰勒斯曾经利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成的两个相似三角形来测量金字塔的高度.如图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO. 【求助交流】 如图,为了估算河的宽度,我们可以在河对岸选定一个目标P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS = 45 m,ST = 90 m,QR = 60 m,求河的宽度PQ. 【补助练兵】 已知左、右并排的两棵大树的高分别是AB = 8 m和CD = 12 m,两树根部的距离BD = 5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C? 【共助反馈】 在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米? 小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高? 3.小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
续助反思
课题 27.2.3相似三角形的周长与面积 课型 新授 主备
审核 班级 姓名 时间
学习 目标 1、理解并初步掌握相似三角形周长与面积的性质. 2、通过把实际问题转换化成数学模型,体会从特殊到一般的认识问题的方法. 3、通过对性质的发现和论证,提高数学学习热情,增强探究意识.
重点 相似三角形的性质与运用.
难点 相似三角形性质的灵活运用.
学习过程 学(教)记录
【自助学习】 已知: ?ABC∽?A’B’C’,根据相似的定义,我们有哪些结论? 问:两个三角形相似,除了对应边成比例、对应角相等之外,我们还可以得到哪些结论? 2.思考:(1)如果两个三角形相似,它们的周长之间有什么关系? (2)如果两个三角形相似,它们的面积之间有什么关系? (3)两个相似多边形的周长和面积分别有什么关系? 【互助探究】 已知:如图:△ABC ∽△A′B′C′,它们的周长分别是 60 cm 和72 cm,且AB=15 cm,B′C′=24 cm,求BC、AB、A′B′、A′C′的长. 【求助交流】 在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是12,求ΔDEF的周长和面积。 【补助练兵】 1.填空: (1)如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为_____,面积的比为_____. (2)如果两个相似三角形面积的比为3∶5 ,那么它们的相似比为________,周长的比为________. (3)连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______. (4)两个相似三角形对应的中线长分别是6 cm和18 cm,若较大 三角形的周长是42 cm ,面积是12 cm 2,则较小三角形的周长为________cm,面积为_______cm2. 2.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比. 【共助反馈】已知:如图,△ABC中,DE∥BC,
(1)若,① 求的值; ② 求的值; ③ 若,求△ADE的面积; (2)若,,过点E作EF∥AB交BC于F,求□BFED的面积;
续助反思
