苏教版选修2-1课件: 3.2.3 空间的角的计算 课件(25张)
文档属性
| 名称 | 苏教版选修2-1课件: 3.2.3 空间的角的计算 课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-16 00:00:00 | ||
图片预览


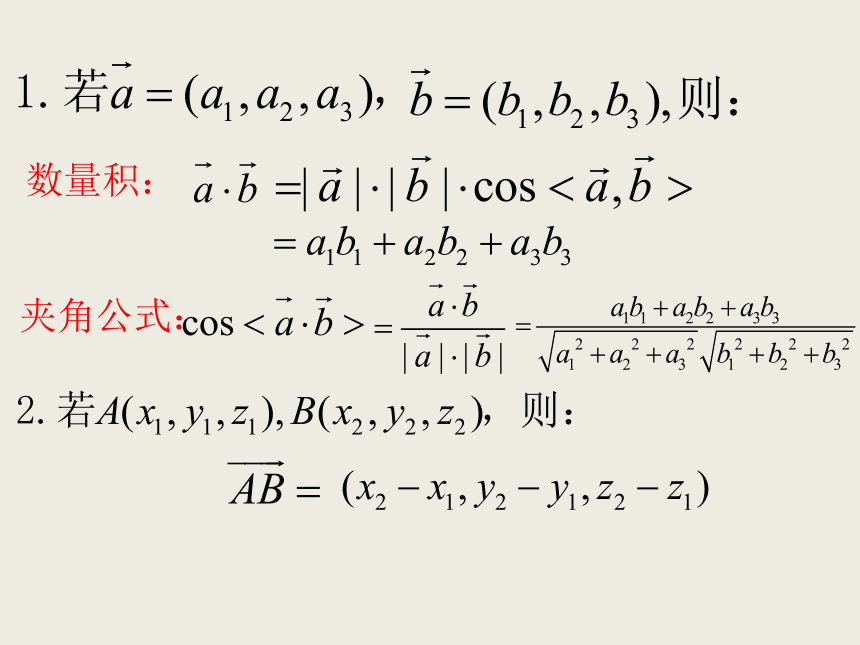


文档简介
课件25张PPT。3.2.3
利用向量解决
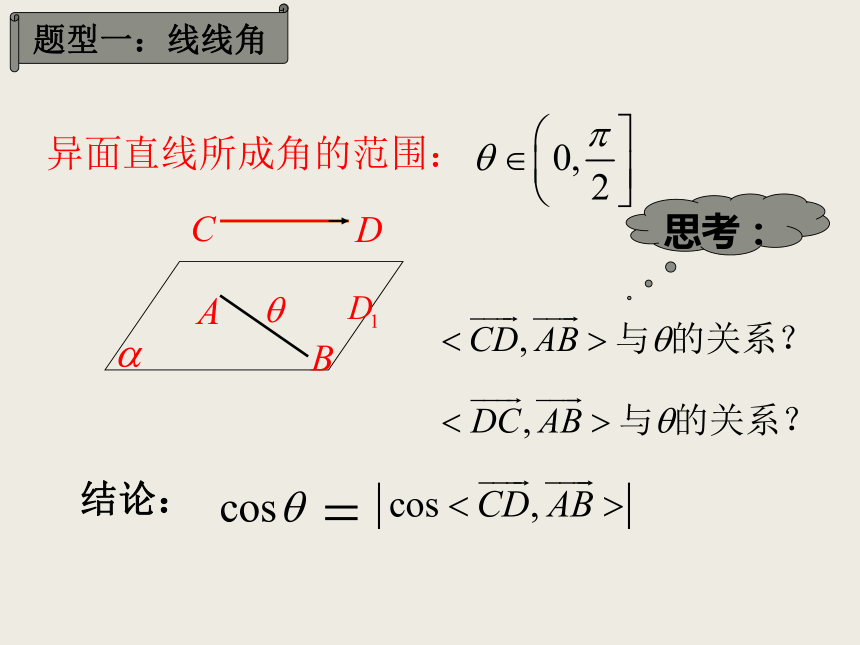
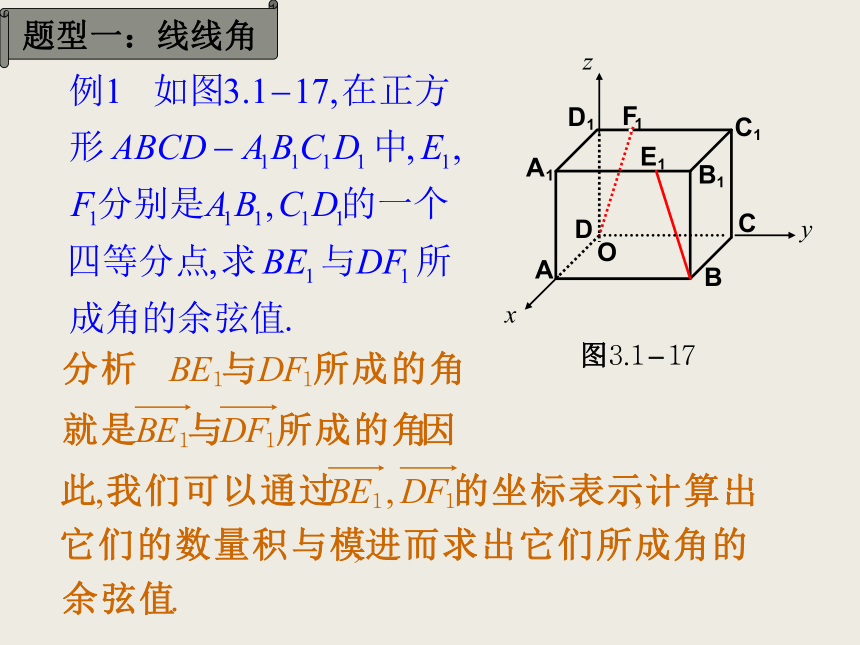
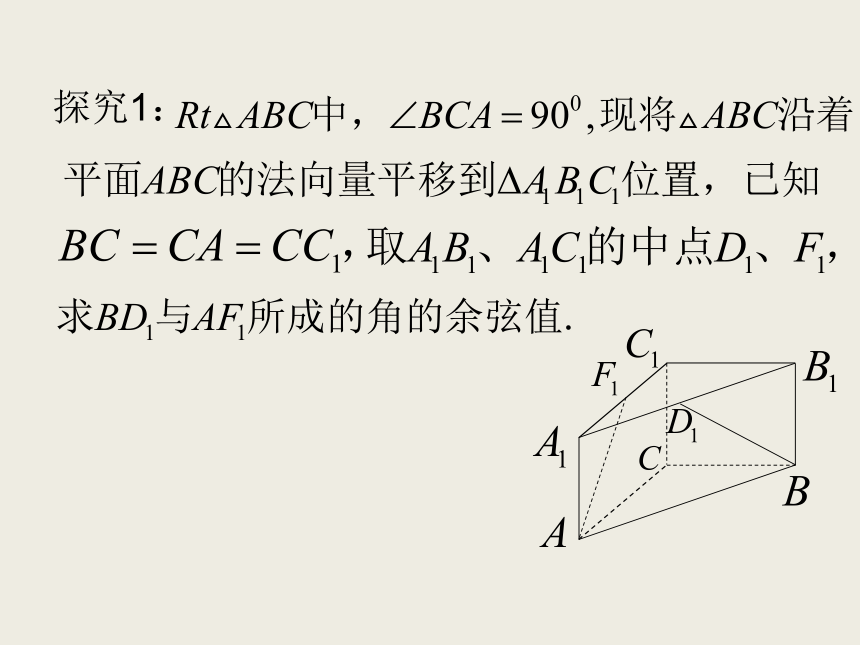
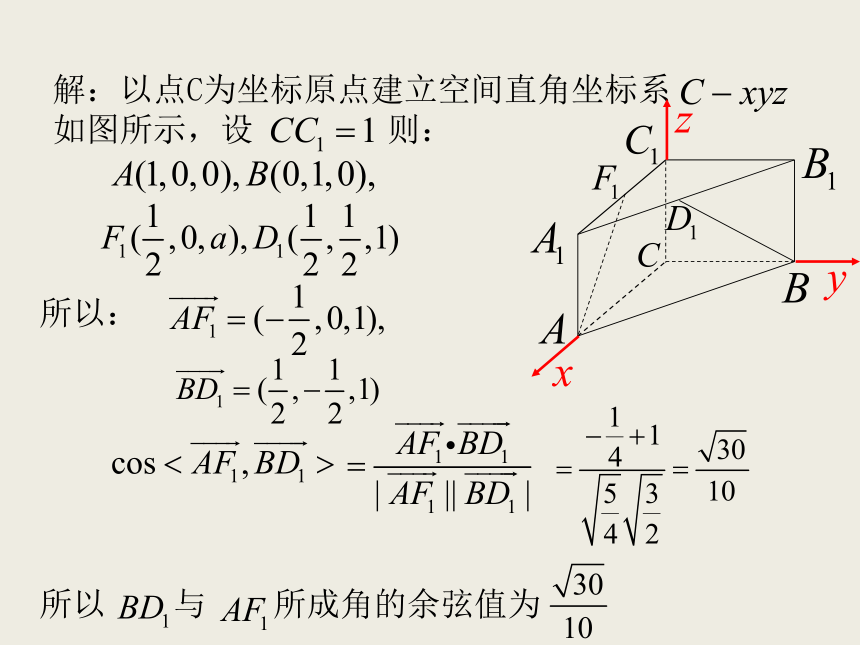
空间角问题 空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而避免了一些繁琐的推理论证。求空间角与距离是立体几何的一类重要的问题,也是高考的热点之一。本节课主要是讨论怎么样用向量的办法解决空间角问题。数量积: 夹角公式: 异面直线所成角的范围: 思考:结论:探究1:解:以点C为坐标原点建立空间直角坐标系 如图所示,设 则: 所以:所以 与 所成角的余弦值为练习:在长方体 中,直线与平面所成角的范围: 思考:结论:直线AB与平面α所成的角θ可
看成是向量与平面α
的法向量所成的锐角
的余角,所以有 探究二:在长方体 中,练习:
的棱长为1.正方体二面角的范围:关键:观察二面角的范围设平面立体几何中的向量方法——坐标法例四:已知:△ABC为正三角形,EC⊥平面ABC,且EC,DB在平面ABC同侧,CE=CA=2BD.求证:
平面ADE⊥平面ACE.⑴怎样建立适当的空间直角坐标系?⑵怎样证明平面ADE⊥平面ACE?⑹如何求平面ADE、平面ACE的法向量?⑶一个平面的法向量有多少个?⑷能否设平面ADE的法向量为
n=(1,y,z)?⑸这样做有什么好处?解:分别以CB,CE所在直线为y,z轴,C为原点建立空间直角坐标系C-xyz,如右下图,设正三角形ABC边长为2则C(0,0,0)、E(0,0,2)、D(0,2,1)、B(0,2,0)、设N为AC中点,则N 连接
BN,∵△ABC为正三角形,∴BN⊥AC,∵EC⊥平面ABC, ∴BN⊥EC,又AC∩EC=C, ∴BN ⊥平面ACE.因此可取向量 为平面
ACE的法向量.那么
设平面ADE的法向量为n=(1,y,z),则
n
n
∴n=∵ n∴平面DEA⊥平面ACE.
为了方便计算,能否取平面ACE的法向量为通过上例,你能说出用坐标法解决立体几何中问题的一般步骤吗?步骤如下:
1.建立适当的空间直角坐标系;
2.写出相关点的坐标及向量的坐标;
3.进行相关的计算;
4写出几何意义下的结论.小结:1.异面直线所成角: 2.直线与平面所成角: 3.二面角:关键:观察二面角的范围
利用向量解决
空间角问题 空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而避免了一些繁琐的推理论证。求空间角与距离是立体几何的一类重要的问题,也是高考的热点之一。本节课主要是讨论怎么样用向量的办法解决空间角问题。数量积: 夹角公式: 异面直线所成角的范围: 思考:结论:探究1:解:以点C为坐标原点建立空间直角坐标系 如图所示,设 则: 所以:所以 与 所成角的余弦值为练习:在长方体 中,直线与平面所成角的范围: 思考:结论:直线AB与平面α所成的角θ可
看成是向量与平面α
的法向量所成的锐角
的余角,所以有 探究二:在长方体 中,练习:
的棱长为1.正方体二面角的范围:关键:观察二面角的范围设平面立体几何中的向量方法——坐标法例四:已知:△ABC为正三角形,EC⊥平面ABC,且EC,DB在平面ABC同侧,CE=CA=2BD.求证:
平面ADE⊥平面ACE.⑴怎样建立适当的空间直角坐标系?⑵怎样证明平面ADE⊥平面ACE?⑹如何求平面ADE、平面ACE的法向量?⑶一个平面的法向量有多少个?⑷能否设平面ADE的法向量为
n=(1,y,z)?⑸这样做有什么好处?解:分别以CB,CE所在直线为y,z轴,C为原点建立空间直角坐标系C-xyz,如右下图,设正三角形ABC边长为2则C(0,0,0)、E(0,0,2)、D(0,2,1)、B(0,2,0)、设N为AC中点,则N 连接
BN,∵△ABC为正三角形,∴BN⊥AC,∵EC⊥平面ABC, ∴BN⊥EC,又AC∩EC=C, ∴BN ⊥平面ACE.因此可取向量 为平面
ACE的法向量.那么
设平面ADE的法向量为n=(1,y,z),则
n
n
∴n=∵ n∴平面DEA⊥平面ACE.
为了方便计算,能否取平面ACE的法向量为通过上例,你能说出用坐标法解决立体几何中问题的一般步骤吗?步骤如下:
1.建立适当的空间直角坐标系;
2.写出相关点的坐标及向量的坐标;
3.进行相关的计算;
4写出几何意义下的结论.小结:1.异面直线所成角: 2.直线与平面所成角: 3.二面角:关键:观察二面角的范围
