人教版数学七年级下册 5.2平行线及其判定 同步练习
文档属性
| 名称 | 人教版数学七年级下册 5.2平行线及其判定 同步练习 | 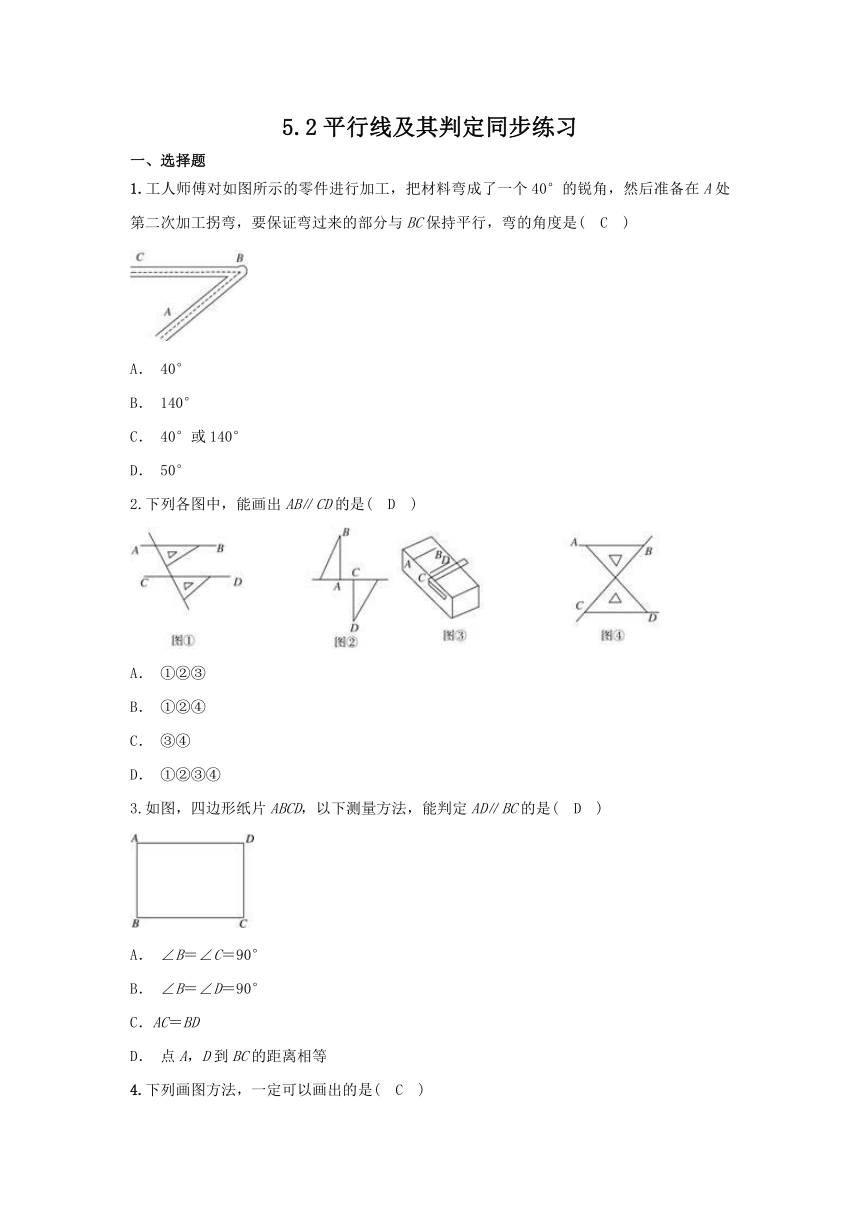 | |
| 格式 | zip | ||
| 文件大小 | 87.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-18 10:18:52 | ||
图片预览



文档简介
5.2平行线及其判定同步练习
选择题
1.工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( C )
A. 40°
B. 140°
C. 40°或140°
D. 50°
2.下列各图中,能画出AB∥CD的是( D )
A. ①②③
B. ①②④
C. ③④
D. ①②③④
3.如图,四边形纸片ABCD,以下测量方法,能判定AD∥BC的是( D )
A. ∠B=∠C=90°
B. ∠B=∠D=90°
C.AC=BD
D. 点A,D到BC的距离相等
4.下列画图方法,一定可以画出的是( C )
A. 过点P画线段CD,使线段CD与已知线段AB相交
B. 过点P画线段CD,使线段CD与已知射线AB相交
C. 过射线AB外一点P画直线CD,使CD∥AB
D. 过直线AB外一点P画射线CD,使AB与CD相交
5.下列说法正确的是( D )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
6.已知直线a、b、c在同一平面内,则下列说法错误的是( C )
A. 如果a∥b,b∥c,那么a∥c
B.a⊥b,c⊥b,那么a∥c
C. 如果a与b相交,b与c相交,那么a与c一定相交
D. 如果a与b相交,b与c不相交,那么a与c一定相交
7.如图,能判定 的条件是( ?D?)
A. B. C. D.
8.如图,BD⊥BC,∠1=40°,若使AB∥CD,则∠2的度数是( C )
A. 30°
B. 40°
C. 50°
D. 60°
9. 如图,下列条件中:
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.能判定AB∥CD的条件个数有( C )
A.1 B.2 C.3 D.4
10.如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( C )
A. 8°
B. 10°
C. 18°
D. 28°
11.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( A )
A. 第一次左拐30°,第二次右拐30°
B. 第一次右拐50°,第二次左拐130°
C. 第一次右拐50°,第二次右拐130°
D. 第一次向左拐50°,第二次向左拐120°
12.如图,以下条件能判定GE∥CH的是( C )
A、∠FEB=∠ECD B、∠AEG=∠DCH C、∠GEC=∠HCF D、∠HCE=∠AEG
12.如图,在下列条件中,不能判定直线a与b平行的是( C )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠5 D.∠3+∠4=180°
二、填空题
11.如图所示,AB∥CD,EF与AB,CD相交,EF与AB交于点_____,
EF与CD交于______.
【答案】M N
12.(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
【答案】经过直线外一点,有且只有一条直线与这条直线平行 平行于同一直线的两条直线平行
13. 如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________ .
【答案】a∥b
14.如图,请你添加一个条件________,使AB∥CD.
【答案】∠1=∠5
15.工人师傅在架设电线时,为了检验三条电线是否互相平行只检查了其中两条是否与第三条平行即可,这样做的道理是______________________________.
【答案】平行于同一条直线的两条直线互相平行
16.如图是一个平行四边形,请用符号表示图中的平行线:__________________.
【答案】AB∥CD,AD∥BC
三、解答题
17.如图所示,在∠AOB内有一点P.
(1)过P画L1∥OA;(2)过P画L2∥OB;
(3)用量角器量一量L1与L2相交的角与∠O的大小有怎样关系?
答案:(1),(2)如图所示,(3)L1与L2夹角有两个,∠1,∠2,∠1=∠O,∠2+∠O=180°,所以L1和L2夹角与∠O相等或互补.
18.AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
【答案】BE∥DF,
∵AB⊥BC,∴∠ABC=90°,即∠3+∠4=90°.
又∵∠1+∠2=90°,且∠2=∠3,∴∠1=∠4,
理由是:等角的余角相等,∴BE∥DF.
理由是:同位角相等,两直线平行.
19. 如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD;
(2)试判断BM与DN是否平行,为什么?
解:(1)∵AB⊥EF,CD⊥EF,
∴AB∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行).
(2)BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°(垂直的定义).
∵∠1=∠2,
∴∠ABE-∠1=∠CDE-∠2,
即∠MBE=∠NDE.
∴BM∥DN(同位角相等,两直线平行)
20.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
【答案】证明 ∵GH⊥CD,(已知)
∴∠CHG=90°.(垂直定义)
又∵∠2=30°,(已知)
∴∠3=60°.
∴∠4=60°.(对顶角相等)
又∵∠1=60°,(已知)
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
21. 如图,已知:∠B=∠D+∠E,试说明:AB∥CD.
解:∵∠BFD=∠D+∠E,
又∵∠B=∠D+∠E,
∴∠B=∠BFD,
∴AB∥CD.
22.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
【答案】CD∥AB;
理由:
∵CD∥EF,EF∥AB,
∴CD∥AB.
23.如图,已知∠1=30°,∠B=60°,AB⊥AC。
(1)计算:∠DAB+∠B
(2)AB与CD平行吗?AD与BC平行吗?
答案:(1)180°(2)AD∥BC,AB与CD不平行
选择题
1.工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( C )
A. 40°
B. 140°
C. 40°或140°
D. 50°
2.下列各图中,能画出AB∥CD的是( D )
A. ①②③
B. ①②④
C. ③④
D. ①②③④
3.如图,四边形纸片ABCD,以下测量方法,能判定AD∥BC的是( D )
A. ∠B=∠C=90°
B. ∠B=∠D=90°
C.AC=BD
D. 点A,D到BC的距离相等
4.下列画图方法,一定可以画出的是( C )
A. 过点P画线段CD,使线段CD与已知线段AB相交
B. 过点P画线段CD,使线段CD与已知射线AB相交
C. 过射线AB外一点P画直线CD,使CD∥AB
D. 过直线AB外一点P画射线CD,使AB与CD相交
5.下列说法正确的是( D )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
6.已知直线a、b、c在同一平面内,则下列说法错误的是( C )
A. 如果a∥b,b∥c,那么a∥c
B.a⊥b,c⊥b,那么a∥c
C. 如果a与b相交,b与c相交,那么a与c一定相交
D. 如果a与b相交,b与c不相交,那么a与c一定相交
7.如图,能判定 的条件是( ?D?)
A. B. C. D.
8.如图,BD⊥BC,∠1=40°,若使AB∥CD,则∠2的度数是( C )
A. 30°
B. 40°
C. 50°
D. 60°
9. 如图,下列条件中:
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.能判定AB∥CD的条件个数有( C )
A.1 B.2 C.3 D.4
10.如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( C )
A. 8°
B. 10°
C. 18°
D. 28°
11.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( A )
A. 第一次左拐30°,第二次右拐30°
B. 第一次右拐50°,第二次左拐130°
C. 第一次右拐50°,第二次右拐130°
D. 第一次向左拐50°,第二次向左拐120°
12.如图,以下条件能判定GE∥CH的是( C )
A、∠FEB=∠ECD B、∠AEG=∠DCH C、∠GEC=∠HCF D、∠HCE=∠AEG
12.如图,在下列条件中,不能判定直线a与b平行的是( C )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠5 D.∠3+∠4=180°
二、填空题
11.如图所示,AB∥CD,EF与AB,CD相交,EF与AB交于点_____,
EF与CD交于______.
【答案】M N
12.(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
【答案】经过直线外一点,有且只有一条直线与这条直线平行 平行于同一直线的两条直线平行
13. 如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________ .
【答案】a∥b
14.如图,请你添加一个条件________,使AB∥CD.
【答案】∠1=∠5
15.工人师傅在架设电线时,为了检验三条电线是否互相平行只检查了其中两条是否与第三条平行即可,这样做的道理是______________________________.
【答案】平行于同一条直线的两条直线互相平行
16.如图是一个平行四边形,请用符号表示图中的平行线:__________________.
【答案】AB∥CD,AD∥BC
三、解答题
17.如图所示,在∠AOB内有一点P.
(1)过P画L1∥OA;(2)过P画L2∥OB;
(3)用量角器量一量L1与L2相交的角与∠O的大小有怎样关系?
答案:(1),(2)如图所示,(3)L1与L2夹角有两个,∠1,∠2,∠1=∠O,∠2+∠O=180°,所以L1和L2夹角与∠O相等或互补.
18.AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
【答案】BE∥DF,
∵AB⊥BC,∴∠ABC=90°,即∠3+∠4=90°.
又∵∠1+∠2=90°,且∠2=∠3,∴∠1=∠4,
理由是:等角的余角相等,∴BE∥DF.
理由是:同位角相等,两直线平行.
19. 如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD;
(2)试判断BM与DN是否平行,为什么?
解:(1)∵AB⊥EF,CD⊥EF,
∴AB∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行).
(2)BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°(垂直的定义).
∵∠1=∠2,
∴∠ABE-∠1=∠CDE-∠2,
即∠MBE=∠NDE.
∴BM∥DN(同位角相等,两直线平行)
20.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
【答案】证明 ∵GH⊥CD,(已知)
∴∠CHG=90°.(垂直定义)
又∵∠2=30°,(已知)
∴∠3=60°.
∴∠4=60°.(对顶角相等)
又∵∠1=60°,(已知)
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
21. 如图,已知:∠B=∠D+∠E,试说明:AB∥CD.
解:∵∠BFD=∠D+∠E,
又∵∠B=∠D+∠E,
∴∠B=∠BFD,
∴AB∥CD.
22.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
【答案】CD∥AB;
理由:
∵CD∥EF,EF∥AB,
∴CD∥AB.
23.如图,已知∠1=30°,∠B=60°,AB⊥AC。
(1)计算:∠DAB+∠B
(2)AB与CD平行吗?AD与BC平行吗?
答案:(1)180°(2)AD∥BC,AB与CD不平行
