人教A版高中数学 选修2-1 3.1.1空间向量及其加减运算 课件 共55张PPT
文档属性
| 名称 | 人教A版高中数学 选修2-1 3.1.1空间向量及其加减运算 课件 共55张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-18 10:01:30 | ||
图片预览









文档简介
课件55张PPT。空间向量
及其加减运算 用字母 等或者用有向线段
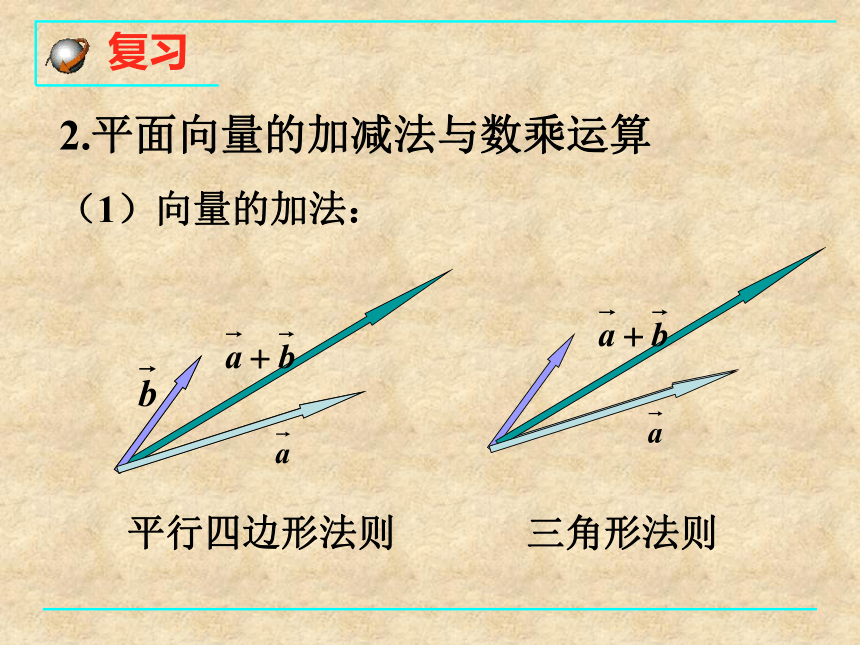
的起点与终点字母 表示.⒈定义:既有大小又有方向的量叫向量. 几何表示法:用有向线段表示; 字母表示法:相等的向量: 长度相等且方向相同的向量. 复习2.平面向量的加减法与数乘运算(1)向量的加法:平行四边形法则三角形法则 复习(2)向量的减法三角形法则3. 平面向量的加法运算律加法交换律:加法结合律: 复习平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量的加法、减法运算空间向量具有大小和方向的量加法交换律加法结合律加法交换律加法:三角形法则或
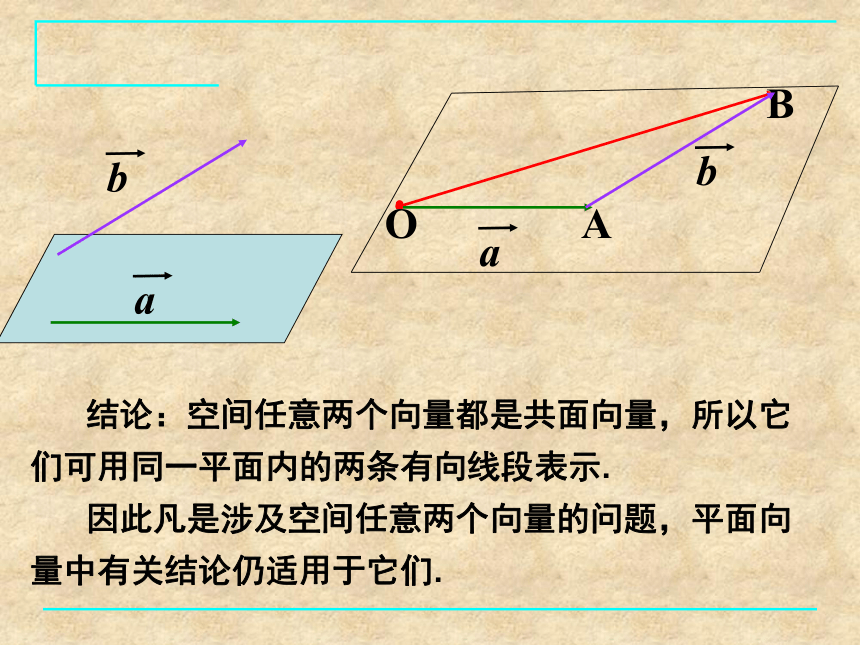
平行四边形法则减法:三角形法则加法结合律成立吗?OABC空间向量的加减法OAB 结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们. 平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量的加法、减法运算空间向量具有大小和方向的量加法交换律加法结合律加法交换律加法:三角形法则或
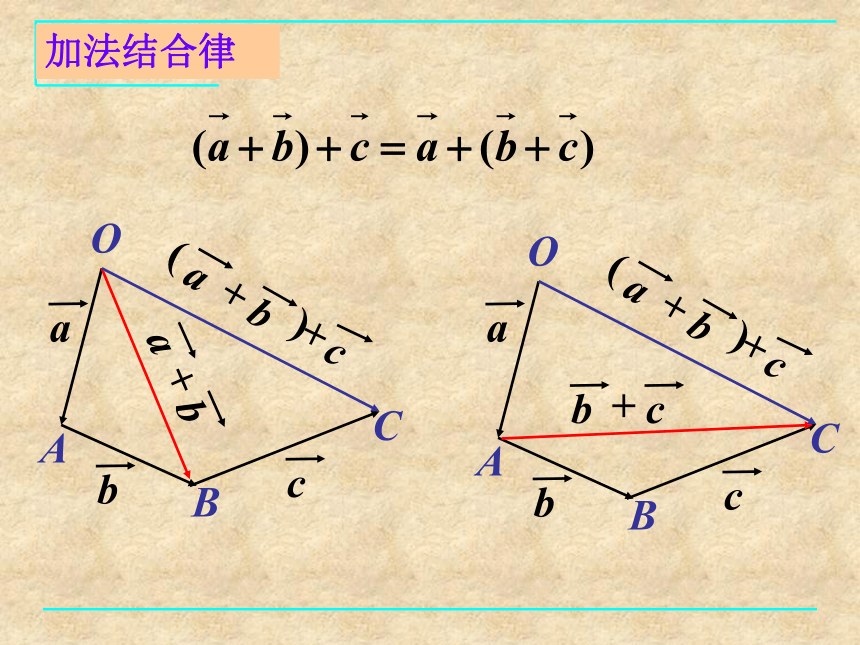
平行四边形法则减法:三角形法则加法结合律成立吗?OABCOABC加法结合律(1)加法交换律:(2)加法结合律:abca + b + c abca + b + c a + b b + c 空间向量的加法、减法运算对空间向量的加法、减法的说明⒈ 空间向量的运算就是平面向量运算的推广.⒉ 两个向量相加的平行四边形法则在空间
仍然成立.⒊ 空间向量的加法运算可以推广至若干个
向量相加. 说明(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即: 推广(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即: 推广A’B’C’D’ 平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱. 平行四边形ABCD平移向量 a 到 的轨迹所形成的几何体,叫做平行六面体.记作ABCD— . 平行六面体例 例题解: 例题ABMCGD 空间四边形ABCD中,M、G分别是BC、CD边的中点,化简: 练习ABMCGD(2)原式 练习参考答案3.1.2 空间向量的数乘运算———共线向量与共面向量平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律类比思想 数形结合思想数乘:ka,k为正数,负数,零OB结论:空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
一、空间向量数乘运算1.实数 与空间向量 的乘积 仍然是一个向量.当 时, 当 时, 与向量 方向相同; 与向量 方向相同; 是零向量.当 时,(1)方向:(2)大小: 的长度是 的长度的 倍.2.空间向量的数乘运算满足分配律及结合律问题:平面向量中,的充要条件是:存在唯一的实数 ,使能否推广到空间向量中呢?零向量与任意向量共线.作用:由此可判断空间中两直线平行或三点共线问题 共线向量定理:
对空间任意两个向量 , 。
存在实数λ,使如图,l 为经过已知点A且平行已知非零向量 的直线,对空间任意一点O,所以即 若在l上取 则有①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.lABPO若点P是直线l上任意一点,则 由 知存在唯一的t, 满足①②因为 所以 特别的,当t = 时,则有ABPO进一步,t1-tP点为A,B 的中点练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线A、B、P三点共线AOABP三、共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面 如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有 那么什么情况下三个向量共面呢?反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?C2.共面向量定理:如果两个向量 , 不共线, 则向量 与向量 , 共面的充要条件是存在实数对x,y使推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x, y,使C对空间任一点O,有填空:1-x-yxyC③ 式称为空间平面ABC的向量表示式,空间中任意平面由空 间一点及两个不共线的向量唯一确定.③作用:由此可判断空间任意四点共面P与A,B,C共面例1. 已知A、B、C三点不共线,对于平面ABC外的任一点O,确定在下列各条件下,点P是否与A、B、C一定共面?例2. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
OBAHGFECD小结共面?2.空间向量的数乘运算2. 空间向量的数乘运算空间向量的数乘运算满足分配律及结合律OAPB点P在直线L上点P在直线L上 已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值.在正方体AC1中,点E是面AC’ 的中心,
若 ,求实数x,y.共面向量:平行于同一平面的向量,叫做共面向量. 已知平行四边形ABCD,从平面AC外一点O引向量 , ,
,求证:
(1)?四点E、F、G、H共面;
(2)平面EG∥平面AC .ABMCGD 空间四边形ABCD中,M、G分别是BC、CD边的中点,化简:ABMCGD(2)原式空间四边形ABCD中,M、G分别是BC、CD边的中点,化简: 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值. 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值. 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律8.小结类比思想 数形结合思想数乘:ka,k为正数,负数,零
及其加减运算 用字母 等或者用有向线段
的起点与终点字母 表示.⒈定义:既有大小又有方向的量叫向量. 几何表示法:用有向线段表示; 字母表示法:相等的向量: 长度相等且方向相同的向量. 复习2.平面向量的加减法与数乘运算(1)向量的加法:平行四边形法则三角形法则 复习(2)向量的减法三角形法则3. 平面向量的加法运算律加法交换律:加法结合律: 复习平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量的加法、减法运算空间向量具有大小和方向的量加法交换律加法结合律加法交换律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律成立吗?OABC空间向量的加减法OAB 结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们. 平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量的加法、减法运算空间向量具有大小和方向的量加法交换律加法结合律加法交换律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律成立吗?OABCOABC加法结合律(1)加法交换律:(2)加法结合律:abca + b + c abca + b + c a + b b + c 空间向量的加法、减法运算对空间向量的加法、减法的说明⒈ 空间向量的运算就是平面向量运算的推广.⒉ 两个向量相加的平行四边形法则在空间
仍然成立.⒊ 空间向量的加法运算可以推广至若干个
向量相加. 说明(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即: 推广(2)首尾相接的若干向量构成一个封闭图形,
则它们的和为零向量.即: 推广A’B’C’D’ 平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱. 平行四边形ABCD平移向量 a 到 的轨迹所形成的几何体,叫做平行六面体.记作ABCD— . 平行六面体例 例题解: 例题ABMCGD 空间四边形ABCD中,M、G分别是BC、CD边的中点,化简: 练习ABMCGD(2)原式 练习参考答案3.1.2 空间向量的数乘运算———共线向量与共面向量平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律类比思想 数形结合思想数乘:ka,k为正数,负数,零OB结论:空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
一、空间向量数乘运算1.实数 与空间向量 的乘积 仍然是一个向量.当 时, 当 时, 与向量 方向相同; 与向量 方向相同; 是零向量.当 时,(1)方向:(2)大小: 的长度是 的长度的 倍.2.空间向量的数乘运算满足分配律及结合律问题:平面向量中,的充要条件是:存在唯一的实数 ,使能否推广到空间向量中呢?零向量与任意向量共线.作用:由此可判断空间中两直线平行或三点共线问题 共线向量定理:
对空间任意两个向量 , 。
存在实数λ,使如图,l 为经过已知点A且平行已知非零向量 的直线,对空间任意一点O,所以即 若在l上取 则有①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.lABPO若点P是直线l上任意一点,则 由 知存在唯一的t, 满足①②因为 所以 特别的,当t = 时,则有ABPO进一步,t1-tP点为A,B 的中点练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线A、B、P三点共线AOABP三、共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,也可能不共面 如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有 那么什么情况下三个向量共面呢?反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?C2.共面向量定理:如果两个向量 , 不共线, 则向量 与向量 , 共面的充要条件是存在实数对x,y使推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x, y,使C对空间任一点O,有填空:1-x-yxyC③ 式称为空间平面ABC的向量表示式,空间中任意平面由空 间一点及两个不共线的向量唯一确定.③作用:由此可判断空间任意四点共面P与A,B,C共面例1. 已知A、B、C三点不共线,对于平面ABC外的任一点O,确定在下列各条件下,点P是否与A、B、C一定共面?例2. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
OBAHGFECD小结共面?2.空间向量的数乘运算2. 空间向量的数乘运算空间向量的数乘运算满足分配律及结合律OAPB点P在直线L上点P在直线L上 已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值.在正方体AC1中,点E是面AC’ 的中心,
若 ,求实数x,y.共面向量:平行于同一平面的向量,叫做共面向量. 已知平行四边形ABCD,从平面AC外一点O引向量 , ,
,求证:
(1)?四点E、F、G、H共面;
(2)平面EG∥平面AC .ABMCGD 空间四边形ABCD中,M、G分别是BC、CD边的中点,化简:ABMCGD(2)原式空间四边形ABCD中,M、G分别是BC、CD边的中点,化简: 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值. 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值. 在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律8.小结类比思想 数形结合思想数乘:ka,k为正数,负数,零
