1.1 等腰三角形（4）-试卷

1.1 等腰三角形（4）
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题8分）
1．下列条件中，不能得到等边三角形的是（ ）
A．有两个内角是60°的三角形 B．三边都相等的三角形
C．有一个角是60°的等腰三角形 D．有两个外角相等的等腰三角形
2．如图，在△ABC中，AB＝AC，∠C＝60°，D，E分别是边AB，BC上两点，且DE∥AC，下列结论不正确的是（ ）
A．∠A＝60° B．△BDE是等腰三角形
C．BD≠DE D．△BDE是等边三角形
3．三角形三边长分别为a，b，c，它们满足(a－b)2＋|b－c|＝0，则该三角形是（ ）
A．等腰三角形 B．直角三角形 C．等边三角形 D．等腰直角三角形
4．如图，在△ABC中，∠C＝90°，∠B＝30°，AC＝3．若点P是BC边上任意一点，则AP的长不可能是（ ）
A．7 B．5.3 C．4.8 D．3.5
5．如图，在△ABC中，∠BAC=90°，∠B=30°，AC=5cm，AD⊥BC于D，则BD=（ ）
A．10cm B．7.5cm C．8.5cm D．6.5cm
/ / /
第2题图 第4题图 第5题图
二．填空题（共4小题，每题5分）
6．在△ABC中，∠A＝60°，∠C＝60°，则△ABC是________三角形．
7．如图，△ABC中，∠C=90°，∠B=∠BAD=30°，DE⊥AB，若CD=2，则DE= ______ ．
/ / /
第7题图 第8题图 第9题图
8．如图，△ABC为等边三角形，∠1＝∠2，BD＝CE，则△ADE是______三角形．
9．如图，在Rt△ABC中，∠C＝90°，点D为AB的中点，DE⊥AC于点E，∠A＝30°，AB＝12，则DE的长度是____．
三．解答题（共3小题，第10题10分，第11、12题各15分）
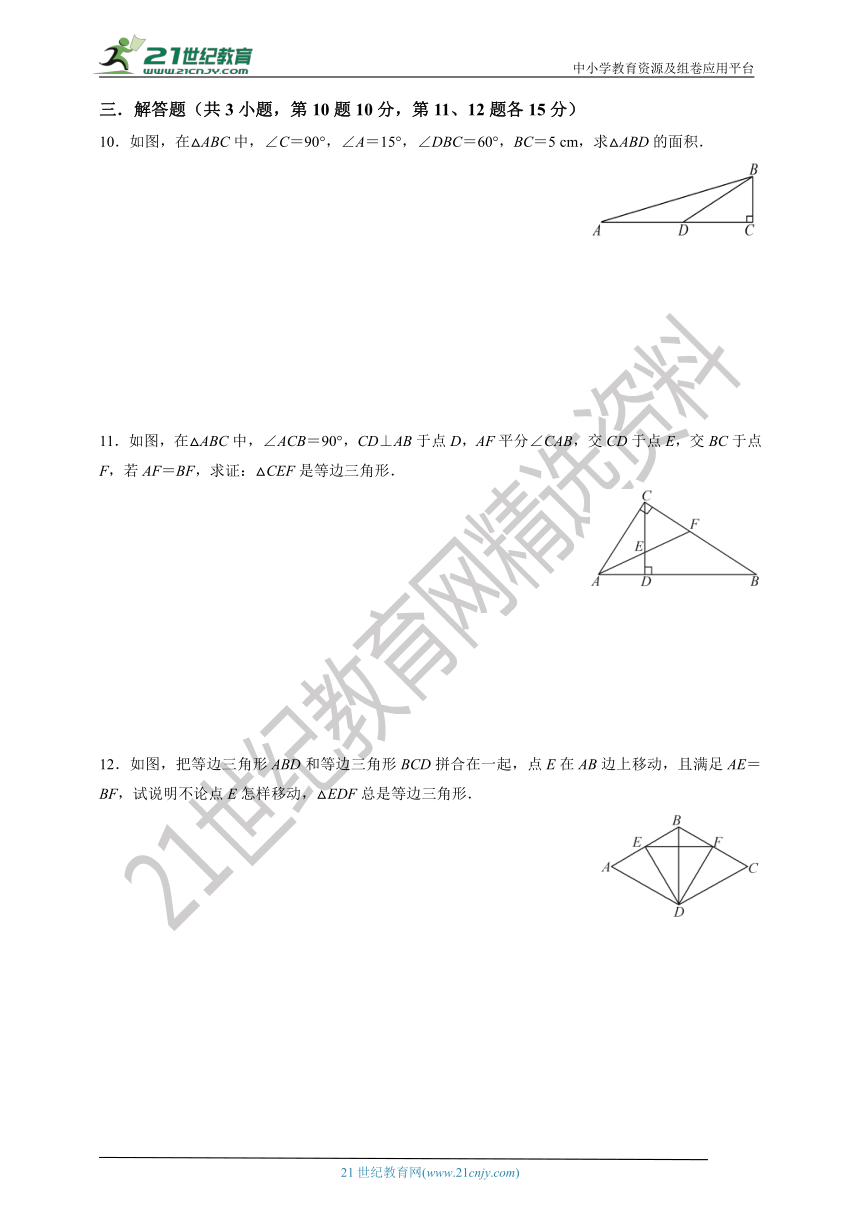
10．如图，在△ABC中，∠C＝90°，∠A＝15°，∠DBC＝60°，BC＝5 cm，求△ABD的面积．
/
11．如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，AF平分∠CAB，交CD于点E，交BC于点F，若AF＝BF，求证：△CEF是等边三角形．
/
12．如图，把等边三角形ABD和等边三角形BCD拼合在一起，点E在AB边上移动，且满足AE＝BF，试说明不论点E怎样移动，△EDF总是等边三角形．
/
试题解析
1．D
【解析】根据等边三角形的定义可知：满足三边相等、有一内角为60°且两边相等或有两个内角为60°中任意一个条件的三角形都是等边三角形．
解：A选项：两个内角为60°，因为三角形的内角和为180°，可知另一个内角也为60°，故该三角形为等边三角形；故本选项不符合题意；B选项：三边都相等的三角形是等边三角形；故本选项不符合题意；C选项：有一个角是60°的等腰三角形是等边三角形；故本选项不符合题意；D选项：两个外角相等说明该三角形中两个内角相等，而等腰三角形的两个底角是相等的，故不能确定该三角形是等边三角形．故本选项符合题意；故选：D．
/
3．C
【解析】根据任意一个数的绝对值都是非负数和偶次方具有非负性可得：a-b=0，b-c=0，再根据三角形的判断方法即可知道该三角形的形状．
解：∵（a-b）2+|b-c|=0，∴a-b=0，b-c=0，∴a=b=c，∴以a，b，c，为三边长的三角形是等边三角形，故选：C．
4．A
【解析】根据直角三角形的性质求出AB的长，再根据AC、AB的值即可得出AP的取值范围，再根据AP的取值范围即可得出答案．
解：∵∠C＝90°，∠B＝30°，
∴AB＝2AC＝6，
∴3≤AP≤6，
故选：A．
5．B
【解析】根据直角三角形的性质求出BC，根据互余关系求出∠CAD=∠B=30°，根据直角三角形的性质求出CD，结合图形计算即可．
解：∵∠BAC=90°，∠B=30°，
∴BC=2AC=10cm，
∵∠BAC=90°，AD⊥BC，
∴∠CAD=∠B=30°，
∴CD=
1
2
AC=2.5cm，
∴BD=BC-CD=7.5cm，
故选B．
6．等边
【解析】利用三角形的内角和180°，求得∠B的度数，进一步判断得出答案即可．
解：∵在△ABC中，∠A＝60°，∠C＝60°，，
∴∠B=180°-∠A-∠C=60°，
∴∠A=∠B=∠C，
∴△ABC是等边三角形，
故答案为：等边．
7．2
【解析】利用已知条件易求∠CAD=30°，则AD的长可求，又因为∠BAD=30°，进而可求出DE的长．
解：∵∠C=90°，∠B=30°，
∴∠CAB=60°，
∵∠B=∠BAD=30°，
∴∠CAD=30°，
∵CD=2，
∴AD=4，
∵∠BAD=30°，
∴DE=
1
2
AD=2，
故答案为：2．
8．等边
【解析】由条件可证明△ABE≌△ACD，从而AE=AD，∠BAC=∠CAE=60°,所以可知△DAE是等边三角形．
证明：∵三角形ABC为等边三角形
∴AB=AC，
在△ABD和△ACE中,
????=????
∠1=∠2
????=????
，
∴△ABD≌△ACE（SAS），
∴AE=AD，∠BAD=∠DAE=60°，
∴△ADE是等边三角形．
9．3
【解析】根据D为AB的中点可求出AD的长，再根据在直角三角形中，30°角所对的直角边等于斜边的一半即可求出DE的长度．
解：∵D为AB的中点，AB=12，∴AD=6，∵DE⊥AC于点E，∠A=30°，∴DE=
1
2
AD=3，故答案是：3．
10．S△ABD＝25cm2．
【解析】先求得AD的长度，再根据S△ABD＝
1
2
AD·BC计算可得.
解：∵∠C＝90°，∠DBC＝60°，
∴∠BDC＝30°，
∴BD＝2BC＝2×5＝10(cm)，
∵∠BDC＝∠A＋∠ABD，
∴∠ABD＝30°－15°＝15°，
∴∠A＝∠ABD，
∴AD＝BD＝10，
∴S△ABD＝
1
2
AD·BC＝
1
2
×10×5＝25(cm2)．
11．证明见解析.
【解析】在△ABC中，AF平分∠CAB、AF=BF求得∠B=∠2=∠1=30°，根据外角性质可得∠4=60°，在Rt△ADE中可得∠3=∠5=60°，进而可知∠4=∠5=60°，得证．
证明：如图，/∵AF是∠BAC的平分线，∴∠CAB=2∠1=2∠2，∵AF=BF，∴∠2=∠B，∵∠ACB=90°，∴∠B+∠CAB=90°，即∠B+2∠1=∠B+2∠2=90°，∴∠B=∠1=∠2=30°，∵∠4是△ABF的外角，∴∠4=∠2+∠B=60°，∵CD是AB边上的高，∴∠2+∠3=90°，∴∠3=60°，∵∠5=∠3，∴∠4=∠5=60°，∴△CEF是等边三角形．
12．证明见解析.
【解析】根据等边三角形性质得出BD=AD，∠CBD=∠A=60°，∠ADB=60°，根据SAS推出△EAD≌△FBD，推出DE=DF，∠ADE=∠BDF，求出∠EDF=60°，根据等边三角形的判定推出即可．
证明：∵△ABD和△BCD是等边三角形，
∴BD＝AD，∠CBD＝∠A＝∠ADB＝60°，
在△EAD和△FBD中，
????＝????
∠??＝∠??????
????＝????
，
∴△EAD≌△FBD,
∴DE＝DF，∠ADE＝∠BDF,
∴∠EDF＝∠BDF＋∠BDE＝∠ADE＋∠BDE＝∠ADB＝60°，
又∵DE＝DF，
∴△EDF是等边三角形．
/