人教版数学七年级下册5.3平行线的性质达标演练
文档属性
| 名称 | 人教版数学七年级下册5.3平行线的性质达标演练 |

|
|
| 格式 | zip | ||
| 文件大小 | 87.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-19 00:00:00 | ||
图片预览

文档简介
人教版数学七年级下册5.3 平行线的性质 达标演练
选择题
1.下列语句中,是命题的是(A)
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④
C.①②⑤ D.②③④⑤
2.(宁波中考)如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为(B)
A.40° B.50° C.60° D.70°
3.下列说法错误的是(C)
A.命题不一定是定理,定理一定是命题
B.定理不可能是假命题
C.真命题是定理
D.如果真命题的正确性是经过推理证实的,这样得到的真命题就是定理
4.下列说法错误的是( A )
A. 所有的命题都是定理. B. 定理是真命题.
C. 公理是真命题. D. “画线段AB=CD”不是命题.
5.下列命题中真命题是(C )
A. 两个锐角之和为钝角 B. 两个锐角之和为锐角
C. 钝角大于它的补角 D. 锐角小于它的余角
6. 如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为(D )
A.20° B.70° C.100° D.110°
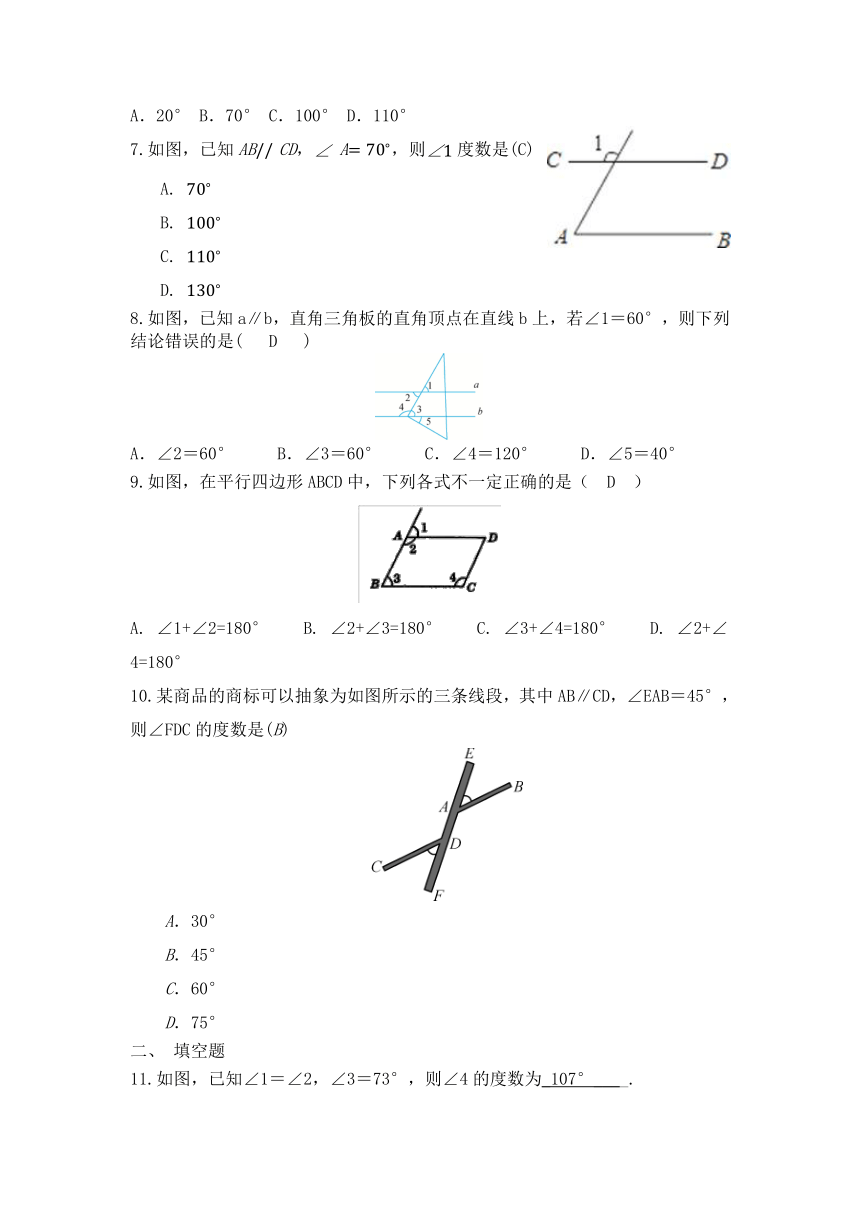
7.如图,已知AB CD, A,则度数是(C)
A.
B.
C.
D.
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( D )
A.∠2=60° B.∠3=60° C.∠4=120° D.∠5=40°
9.如图,在平行四边形ABCD中,下列各式不一定正确的是( D )
A. ∠1+∠2=180° B. ∠2+∠3=180° C. ∠3+∠4=180° D. ∠2+∠4=180°
10.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是(B)
A.30°
B.45°
C.60°
D.75°
填空题
11.如图,已知∠1=∠2,∠3=73°,则∠4的度数为_107°____.
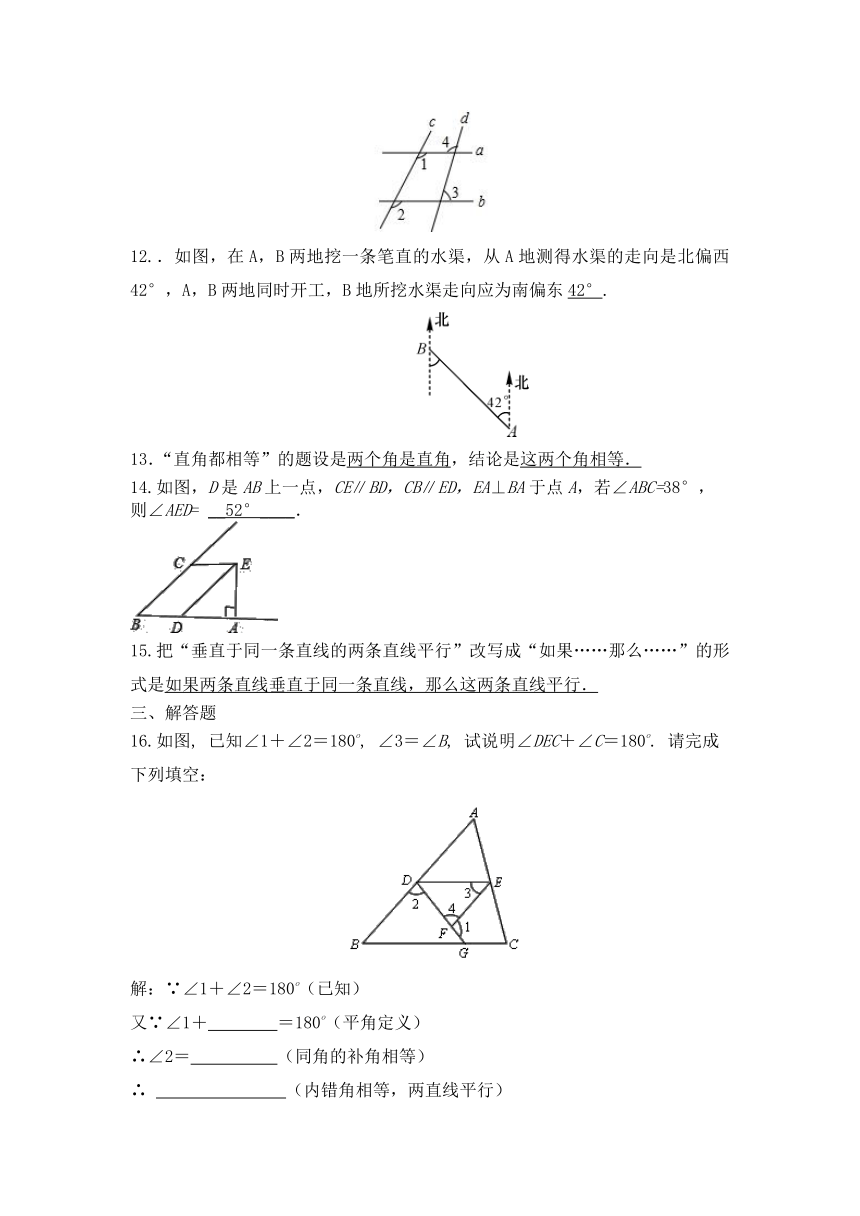
12..如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东42°.
13.“直角都相等”的题设是两个角是直角,结论是这两个角相等.
14.如图,D是AB上一点,CE∥BD,CB∥ED,EA⊥BA于点A,若∠ABC=38°,
则∠AED= __52°____.
15.把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是如果两条直线垂直于同一条直线,那么这两条直线平行.
三、解答题
16.如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)
又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
【解析】试题分析:根据同角的补角可证: ∠2=∠4,再根据内错角相等,两直线平行可证得: AB∥EF , 根据两直线平行,内错角相等可得:∠3=∠ADE,等量代换可得∠ADE=∠B ,
再利用同位角相等两直线平行可得: DE∥BC,利用两直线平行,同旁内角互补可得:∠DEC+∠C =180°.
试题解析:∵∠1+∠2=180°(已知),
又∵∠1+ ∠4 =180°(平角定义),
∴∠2= ∠4 (同角的补角相等),
∴ AB∥EF (内错角相等,两直线平行),
∴∠3= ∠ADE (两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴ ∠ADE=∠B (等量代换),
DE ∥ BC ( 同位角相等,两直线平行 ),
∴∠DEC+∠C =180°( 两直线平行,同旁内角互补 ).
17.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
18.判断下列命题的真假,是假命题的举出反例.
①两个锐角的和是钝角;
②一个角的补角大于这个角;
③不相等的角不是对顶角.
解:①假命题.反例为:30°与40°的和为70°.
②假命题.反例为:120°的补角为60°.
③真命题.
19.如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。试说明:(1)AE∥CF;(2)AB∥CD。
【解析】:就已知条件当中的边角关系,找出符合平行判定的内错角相等,同位角相等,同旁内角互补等判定平行的条件,进行有逻辑的推理和论证,是提高逻辑思维能力的有效方法.
试题解析:(1)∵AD∥CB?(已知)?????
∴ ∠1=∠AEB?(两直线平行,内错角相等)
??又∵∠1=∠2(已知)???
?∴ ∠AEB= ∠2(等量代换)
????∴AE∥CF(同位角相等,两直线平行).
???(2)∵三角形ABE的内角和是180????
∴∠B+∠BAE+∠AEB=180?
又∵∠AEB= ∠2(已证)?∠BAE=∠DCF(已知)
?∴∠B+∠2+∠DCF=180????即∠B+∠BCD=180?
∴AB∥CD(同旁内角互补,两直线平行).
20.如图,CB∥OA,∠C=∠A=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在, 求出其度数;若不存在,说明理由.
解:(1)∵CB∥OA,∴∠AOC=180°-∠C=180°-100°=80°.∵OE平分∠COF,
∴∠COE=∠EOF.∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°.
(2)∠OBC∶∠OFC的值不变.理由如下:
∵CB∥OA,∴∠AOB=∠OBC.
∵∠FOB=∠AOB,∴∠FOB=∠OBC.
∴∠BFO=180°-∠OBC-∠FOB=180°-2∠OBC,
∴∠OFC=180°-∠BFO=2∠OBC,
∴∠OBC∶∠OFC=1∶2.
(3)在三角形COE和三角形AOB中,
∵∠OEC=∠OBA,∠C=∠A,
∴∠COE=∠AOB,
∴OB,OE,OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
选择题
1.下列语句中,是命题的是(A)
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④
C.①②⑤ D.②③④⑤
2.(宁波中考)如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为(B)
A.40° B.50° C.60° D.70°
3.下列说法错误的是(C)
A.命题不一定是定理,定理一定是命题
B.定理不可能是假命题
C.真命题是定理
D.如果真命题的正确性是经过推理证实的,这样得到的真命题就是定理
4.下列说法错误的是( A )
A. 所有的命题都是定理. B. 定理是真命题.
C. 公理是真命题. D. “画线段AB=CD”不是命题.
5.下列命题中真命题是(C )
A. 两个锐角之和为钝角 B. 两个锐角之和为锐角
C. 钝角大于它的补角 D. 锐角小于它的余角
6. 如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为(D )
A.20° B.70° C.100° D.110°
7.如图,已知AB CD, A,则度数是(C)
A.
B.
C.
D.
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( D )
A.∠2=60° B.∠3=60° C.∠4=120° D.∠5=40°
9.如图,在平行四边形ABCD中,下列各式不一定正确的是( D )
A. ∠1+∠2=180° B. ∠2+∠3=180° C. ∠3+∠4=180° D. ∠2+∠4=180°
10.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是(B)
A.30°
B.45°
C.60°
D.75°
填空题
11.如图,已知∠1=∠2,∠3=73°,则∠4的度数为_107°____.
12..如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东42°.
13.“直角都相等”的题设是两个角是直角,结论是这两个角相等.
14.如图,D是AB上一点,CE∥BD,CB∥ED,EA⊥BA于点A,若∠ABC=38°,
则∠AED= __52°____.
15.把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是如果两条直线垂直于同一条直线,那么这两条直线平行.
三、解答题
16.如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)
又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
【解析】试题分析:根据同角的补角可证: ∠2=∠4,再根据内错角相等,两直线平行可证得: AB∥EF , 根据两直线平行,内错角相等可得:∠3=∠ADE,等量代换可得∠ADE=∠B ,
再利用同位角相等两直线平行可得: DE∥BC,利用两直线平行,同旁内角互补可得:∠DEC+∠C =180°.
试题解析:∵∠1+∠2=180°(已知),
又∵∠1+ ∠4 =180°(平角定义),
∴∠2= ∠4 (同角的补角相等),
∴ AB∥EF (内错角相等,两直线平行),
∴∠3= ∠ADE (两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴ ∠ADE=∠B (等量代换),
DE ∥ BC ( 同位角相等,两直线平行 ),
∴∠DEC+∠C =180°( 两直线平行,同旁内角互补 ).
17.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
18.判断下列命题的真假,是假命题的举出反例.
①两个锐角的和是钝角;
②一个角的补角大于这个角;
③不相等的角不是对顶角.
解:①假命题.反例为:30°与40°的和为70°.
②假命题.反例为:120°的补角为60°.
③真命题.
19.如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。试说明:(1)AE∥CF;(2)AB∥CD。
【解析】:就已知条件当中的边角关系,找出符合平行判定的内错角相等,同位角相等,同旁内角互补等判定平行的条件,进行有逻辑的推理和论证,是提高逻辑思维能力的有效方法.
试题解析:(1)∵AD∥CB?(已知)?????
∴ ∠1=∠AEB?(两直线平行,内错角相等)
??又∵∠1=∠2(已知)???
?∴ ∠AEB= ∠2(等量代换)
????∴AE∥CF(同位角相等,两直线平行).
???(2)∵三角形ABE的内角和是180????
∴∠B+∠BAE+∠AEB=180?
又∵∠AEB= ∠2(已证)?∠BAE=∠DCF(已知)
?∴∠B+∠2+∠DCF=180????即∠B+∠BCD=180?
∴AB∥CD(同旁内角互补,两直线平行).
20.如图,CB∥OA,∠C=∠A=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在, 求出其度数;若不存在,说明理由.
解:(1)∵CB∥OA,∴∠AOC=180°-∠C=180°-100°=80°.∵OE平分∠COF,
∴∠COE=∠EOF.∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°.
(2)∠OBC∶∠OFC的值不变.理由如下:
∵CB∥OA,∴∠AOB=∠OBC.
∵∠FOB=∠AOB,∴∠FOB=∠OBC.
∴∠BFO=180°-∠OBC-∠FOB=180°-2∠OBC,
∴∠OFC=180°-∠BFO=2∠OBC,
∴∠OBC∶∠OFC=1∶2.
(3)在三角形COE和三角形AOB中,
∵∠OEC=∠OBA,∠C=∠A,
∴∠COE=∠AOB,
∴OB,OE,OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
